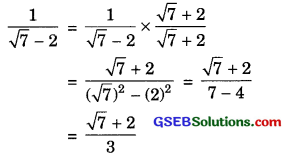Gujarat Board GSEB Solutions Class 10 Maths Chapter 1 Number Systems Ex 1.5 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 1 Number Systems Ex 1.5
Question 1.
Classify the following numbers as rational or irrational.
Solution:
(i) 2 – \(\sqrt{5}\)
(ii) (3 + \(\sqrt{23}\)) – \(\sqrt{23}\)
(iii) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\)
(iv) \(\frac{1}{\sqrt{2}}\)
(v) 2π
Solution:
(i) 2 is a rational number and \(\sqrt{5}\) is an irrational number, then 2 – \(\sqrt{5}\) is an irrational number.
(The difference of rational number and irrational number is an irrational number)
![]()
(ii) (3 + \(\sqrt{23}\)) – \(\sqrt{23}\) = 3 + \(\sqrt{23}\) – \(\sqrt{23}\) = 3 (3 is a rational number)
(iii) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\) = \(\frac { 2 }{ 7 }\) = which is a rational number.
(iv) \(\frac{1}{\sqrt{2}}\)
Here, 1 is rational number and \(\sqrt{2}\) is an irrational number.
∴ The quotient of a non-zero rational number with an irrational number we get an irrational number.
∴ \(\frac{1}{\sqrt{2}}\) is an irrational number.
(v) 2π
Here, 2 is a rational number (2 ≠ 0)
and π is an irrational number.
∴ π is an irrational number.
(Because the product of a non-zero rational number with an irrational number is an irrational number).
![]()
Question 2.
Simplify each of the following expressions:
(i) (3 + \(\sqrt{3}\)) (2 + \(\sqrt{2}\))
(ii) (3 + \(\sqrt{3}\)) (3 – \(\sqrt{3}\))
(iii) (\(\sqrt{5}\) + \(\sqrt{2}\))2
(iv) ( \(\sqrt{5}\) – \(\sqrt{2}\)) (\(\sqrt{5}\) + \(\sqrt{2}\))
Solution:
(i) (3 + \(\sqrt{3}\)) (2 + \(\sqrt{2}\))
= 3(2 + \(\sqrt{2}\)) + \(\sqrt{3}\)(2 + \(\sqrt{2}\))
= 6 + 3\(\sqrt{2}\) + 2\(\sqrt{3}\) + \(\sqrt{3}\) x \(\sqrt{2}\)
= 6 + 3\(\sqrt{2}\) + 2\(\sqrt{3}\) + \(\sqrt{6}\) (-\(\sqrt{a}\) x \(\sqrt{b}\) = \(\sqrt{ab}\))
(ii) (3 + \(\sqrt{3}\)) (3 – \(\sqrt{3}\))
= 32 – (\(\sqrt{3}\))2
[(a – \(\sqrt{a}\)) (a + \(\sqrt{b}\)) = a2 – b]
= 9 – 3 = 6
(iii) (\(\sqrt{5}\) + \(\sqrt{2}\))2
= ( \(\sqrt{5}\))2 + 2 \(\sqrt{5}\) x \(\sqrt{2}\) + ( \(\sqrt{2}\))2
= 5 + 2\(\sqrt{10}\) + 2 ( \(\sqrt{a}\) x \(\sqrt{b}\) = \(\sqrt{ab}\))
= 7 + 27\(\sqrt{10}\)
(iv) (\(\sqrt{5}\) – \(\sqrt{2}\)) ( \(\sqrt{5}\) + \(\sqrt{2}\))
= (\(\sqrt{5}\))2 – (\(\sqrt{2}\))2 = 5 – 2 = 3
Question 3.
Recall, n is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = \(\frac { c }{ d }\). This seems to contradict the fact that n is irrational. How will you resolve this contradiction?
Solution:
π = \(\frac { c }{ d }\)
There is no contradiction as either c or d is irrational and hence n is an irrational.
![]()
Question 4.
Represent \(\sqrt{9.3}\) on the number line.
Solution:
We find \(\sqrt{9.3}\) geometrically.
Let x = 79.3
1. Draw a number line and mark point A on it and take a distance AB = 9.3 units.
2. From point B mark a distance of 1 unit and mark the new point C.
3. Draw perpendicular bisector of AC and mark that point as O.
4. Draw a semicircle with centre O and radius OC.
5. Draw perpendicular at the point B which intersect the semicircle at point D then BD = \(\sqrt{9.3}\).
6. Now from B as centre and radius equal to BD, draw an arc which intersects the number line at P. Thus, BP = \(\sqrt{9.3}\)units.
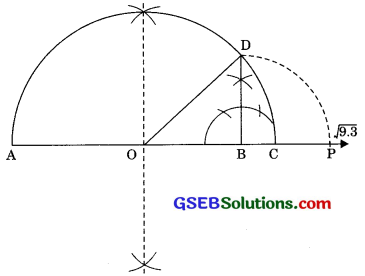
AOBD is a right angled triangle. Also the
radius of circle r = \(\frac { AC }{ 2 }\) i.e., \(\frac { x+1 }{ 2 }\) units.
∴ OC = OD = OA = \(\frac { x+1 }{ 2 }\) units
Now OB = OD = OA = \(\frac { x+1 }{ 2 }\) units
⇒ OB = x – [ \(\frac { x+1 }{ 2 }\) ]
⇒ OB = x – [ \(\frac { x+1 }{ 2 }\) ]
By Pythagoras theorem, we have
BD2 = OD2 – OB2
[ \(\frac { x+1 }{ 2 }\) ]2 – [ \(\frac { x-1 }{ 2 }\) ]2 = \(\frac { 4x }{ 4 }\) = x
∴ BD2 = x
⇒ BD = \(\sqrt{x}\)
Hence BD = \(\sqrt{9.3}\)
⇒ BD = 3.049
![]()
Question 5.
Rationalise the denominators of the following:
(i) \(\frac{1}{\sqrt{7}}\)
(ii) \(\frac{1}{\sqrt{7 – 6}}\)
(iii) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)
(iii) \(\frac{1}{\sqrt{5}+\sqrt{2}}\)
(iv) \(\frac{1}{\sqrt{7}-2}\)
Solution:
(i) We have \(\frac{1}{\sqrt{7}}\)
Multiplying by \(\sqrt{7}\) to numerator and denominator, we get
\(\frac{1}{\sqrt{7}}\) x \(\frac{\sqrt{7}}{\sqrt{7}}\) x \(\frac{\sqrt{7}}{7}\)
(ii) \(\frac{1}{\sqrt{7 – 6}}\)
Multiplying the numerator and denominator by \(\sqrt{7}\) + \(\sqrt{7}\), we get

(iv) \(\frac{1}{\sqrt{7}-2}\)
Multiplying the numerator and denominator by \(\sqrt{7}\) + 2, we get