Gujarat Board GSEB Solutions Class 9 Maths Chapter 10 Circles Ex 10.6 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 10 Circles Ex 10.6
Question 1.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Solution:
Given: Two intersecting circles with centres A and B. Their points of intersection are P and Q.
To prove: ∠APB = ∠AQB

Proof: In ΔAPB and ΔAQB,
AP = AQ [Radii of a circle]
BP = BQ [Radiiofacircle]
AB = AB [Common]
∴ ΔAPB = ΔAQB [SSS Rule]
∴ ∠APB = ∠AQB [CPCT]
![]()
Question 2.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Solution:
Let the radius of the circle be r cm. Let 0M = x cm.
Then ON = (6 – x)cm
∴ OM ⊥ CD
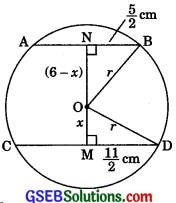
∴ M is the mid-point of CD.
[The perpendicular from the centre of a circle to a chord bisects the chord]
∴ MD = MC = \(\frac {1}{2}\)CD = \(\frac {1}{2}\)(11)cm = \(\frac {11}{2}\)cm
∴ ON ⊥ AB
∴ N is the mid-point of AB.
[The perpendicular from the centre of a circle to a chord bisects the chord]
∴ NB = AN = \(\frac {1}{2}\) AB = \(\frac {1}{2}\)(5) = \(\frac {5}{2}\)cm
In right triangle ONB,
OB2 = ON2 + NB2 [By Pythagoras Theorem]
⇒ r2 = (6 – x)2 + \(\frac {5}{2}\)2 ………..(1)
In right triangle OMD,
OD2 = OM2 + MD2 [By Pythagoras Theorem]
⇒ r2 = x2 + \(\frac {11}{2}\)2 …………(2)
From (1) and (2), we get
(6 – x)2 + \(\frac {5}{2}\)2 = x2 + \(\frac {11}{2}\)2 +
⇒ 36 – 12 x + x2 + \(\frac {25}{4}\) = x2 + \(\frac {121}{4}\)
⇒ 12 x = 36 + \(\frac {25}{4}\) – \(\frac {121}{4}\)
⇒ 12 x = 12
⇒ x = \(\frac {12}{12}\) = 1
Putting x = 1 in (2), we get
r2 = (1)2 + \(\frac {11}{2}\)2 = 1 + \(\frac {121}{4}\)2 = \(\frac {125}{4}\)
⇒ r = \(\frac{5 \sqrt{5}}{2}\)
Hence, the radius of the circle is \(\frac{5 \sqrt{5}}{2}\) cm.
![]()
Question 3.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
Solution:
Case I: When the two chords are on the same side of the centre.
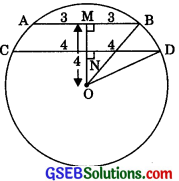
OM ⊥ AB
∴ M is the mid-point of AB.
[The perpendicular from the centre of a circle to a chord bisects the chord]
∴ BM = AM = \(\frac {1}{2}\)(6) = 3cm.
∴ ON⊥ CD
∴ N is the mid-point of CD.
[The perpendicular from the centre of a circle to a chord bisects the chord.]
∴ ON = CN = \(\frac {1}{2}\)CD = \(\frac {1}{2}\)(8) = 4cm
In right triangle OMB,
OB2 = OM2 + MB2 [By Pythagoras theorem]
= (4)2 + (3)2
= 16 + 9 = 25
OB = \(\sqrt{25}\) = 5cm
∴ OD = OB = 5cm [Radiiofacircle]
In right triangle OND,
OD2 = ON2 + ND2 [By Pythagoras theorem]
⇒ (5)2 = ON2 + (4)2
⇒ 25 = ON2 + 16
⇒ ON2 = 25 – 16
⇒ ON2 = 9
⇒ ON = \(\sqrt{9}\) = 3 cm
Hence, the distance of the other chord from the centre is 3 cm.
![]()
Case II: When the two chords are on opposite sides of the centre.
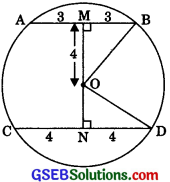
As in case I:
ON = 3 cm.
Question 4.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Solution:
To prove: ∠ABC = \(\frac {1}{2}\)(∠DOE – ∠AOC)
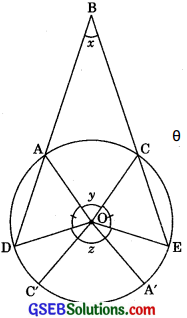
Proof: Let ∠ABC = x, ∠AOC = y and ∠DOE = z.
∠C’OD + ∠A’OE = z – y …………(1)
Let ∠C’OD = θ
then ∠A’OE = z – y – θ [From (1)]
∠AOD = n – (∠AOC + ∠C’OD)
= π – (y + θ)
∠COE = n – (∠C’OA’ + ∠A’OE)
= π – (y + z – y – θ)
= π – (z – θ)
AD = CE
∠AOD = ∠COE
[Equal chords subtend equal angles at the centre]
∴ π – (y + θ) = n – (z – θ)
y + θ = z – θ
2θ = z – y
θ = \(\frac {z – y}{2}\)
∴ ∠C’OD = \(\frac {z – y}{2}\)
and ∠A’OE = z – y – \(\frac {z – y}{2}\) = \(\frac {z – y}{2}\)
∴ ∠AOD = π – (y + θ)
= π – (y + \(\frac {z – y}{2}\))
= π – (\(\frac {z – y}{2}\)) = ∠COE
In ΔOAD,
∴ OA = OD [Radii of the same circiel]
∴ ∠OAD = ∠ODA
[Angles opposite to the same sides of a triangle are equal]
![]()
In ΔOAD,
∠OAD + ∠ODA + ∠AOD = π
[Sum of all the angles of a triangle is it radians]
= ∠OAD + ∠OAD + π – \(\frac {y + z}{2}\) = π
2∠OAD = \(\frac {y + z}{2}\)
∠OAD = \(\frac {y + z}{2}\)
Similarly, ∠OCE = \(\frac {y + z}{2}\)
∠OAB = n – (\(\frac {y + z}{2}\))
and ∠OCB = n – (\(\frac {y + z}{2}\))
In quadrilateral ΔOCB,
∠ABC + ∠OAB + ∠OCB + ∠AOC = 2π
[Sum of all the angles of a quadrilateral is 2n radians]
x + π – (\(\frac {y – z}{2}\)) + π – (\(\frac {y – z}{2}\)) + y = 2π
x + y = \(\frac {y – z}{2}\)
2x + 2y = y + z
2x = z – y
2x+ 2y = y + z
x = \(\frac {z – y}{2}\)
Hence, the result.
Alternative Method
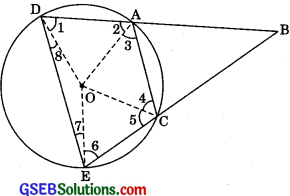
ΔOAC, ΔOCE, ΔOED and ΔODA are isosceles triangles.
∴∠1 = ∠2,∠3 = ∠4,∠5 = ∠6 and ∠7 = ∠8 ……….(1)
In MBC,
∠B + ∠CAB = ∠ACE and ∠B + ∠ACB = ∠CAD
(Exterior angle property)
Adding, 2∠B + ∠CAB + ∠ACB = ∠ACE + ∠CAP
⇒ 2∠B + ∠CED + ∠ADE = ∠ACE + ∠CAD
(∴ Exterior angle of a cyclic quadrilateral is interior opposite angle,
∴ ∠CAB = ∠CED and ∠ACB = ∠ADE)
⇒ 2∠B + (∠6 + ∠7) + (∠1 + ∠8) = (∠4 + ∠5) + (∠2 + ∠3) (Using eqn (1))
⇒ 2∠B + (∠7 + ∠8) = (∠3 + ∠4)
⇒ 2∠B + 1800 – ∠DOE = 1800 – ∠AOC (Angle sum property)
⇒ 2∠B = ∠DOE – ∠AOC
∴ ∠B = \(\frac {1}{2}\)(∠DOE – ∠AOC)
![]()
Question 5.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Solution:
Given: ABDC is a rhombus. E is the point of intersection of its diagonals.
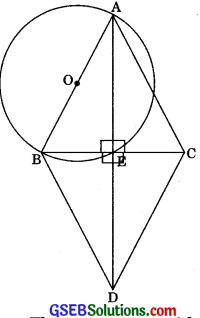
To Prove: The circle drawn with any side, say AB of rhombus ABCD, as a diameter passes through the point E.
Proof: ∠AEB = ∠AEC = ∠CED = ∠BED = 900
(As diagonals of a rhombus bisect each other at right angles)
Now, ∠AEB = 900 and AB is diameter so E must lie on the semicircle.
E is the point of intersection of diagonals.
Hence, the circle drawn with AB as diameter passes through point E.
Similarly, we can prove that the circle is drawn with AC as diameter passes through point E which is the point of intersection of its diagonals.
![]()
Question 6.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Solution:
Given ABCD is a parallelogram. The circle through A, B and C intersects CD (produced, if necessary) at E.
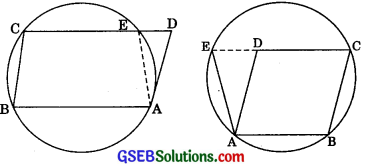
To Prove: AE = AD
Proof: In cyclic quadrilateral ABCE,
∠AED + ∠ABC = 180° ………….(1)
[∴ Opposite angles of a cyclic quadrilateral are supplementary]
Also, ∠ADE + ∠ADO = 180° [Linear Pair Axiom]
But ∠ADO = ∠ABC [Opposite angles of a || gm]
∴ ∠ADE + ∠ABC = 180° ………..(2)
From (1) and (2), we have
∠AED + ∠ABC = ∠ADE + ∠ABC
⇒ ∠AED = ∠ADE
∴ In triangle ADE,
AE = AD
[∴ Sides opposite to equal angles of a triangle are equal] Proved
![]()
Question 7.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
Solution:
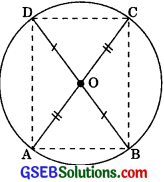
1. Let the chords AC and BD intersect each other at O.
Join AB, BC, CD and DA.
AC and BD bisect each other, so ABCD is a parallelogram
In ΔOAB and ΔOCD,
OA = OC [Given]
OB = OD [Given]
∠AOB = ∠COD [Vert. opp. ∠s]
∴ ΔOAB = ΔOCD [SAS]
∴ AB = CD [CPCT]

BD divides the circle into two equal parts (each a semicircle) so BD is a diameter
Similarly, we can show that AC is a diameter.
2. ∴ ∠A = 90° and ∠C = 90°the angle of a semicircle is 90°.
∠B = 90° and ∠D = 90°
∴ ∠A = ∠B = ∠C = ∠D = 90°
∴ ABCD is a rectangle.
![]()
Question 8.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90° – \(\frac {1}{2}\)A, 90° – \(\frac {1}{2}\) B and 90°- \(\frac {1}{2}\)C.
Solution:
Given: Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively.
To Prove: The angles of the ADEF are 90° – \(\frac {A}{2}\), 9o° – \(\frac {A}{B}\) and 9o° – \(\frac {A}{B}\) respectively.
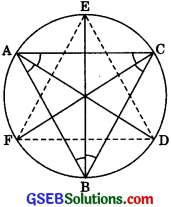
Construction: Join DE, EF and FD.
Proof: ∠FDE = ∠FDA + ∠EDA = ∠PCA + ∠EBA
[∴ Angles in the same segment are equal]
= \(\frac {1}{2}\)∠C + \(\frac {1}{2}\)∠B
⇒ ∠D = \(\frac {∠C + ∠B}{2}\) = \(\frac {180° + ∠A}{2}\)
[∴ In ΔABC,∠A + ∠B + ∠C = 180° [Angle sum property]
= 90° – \(\frac {∠A}{2}\)
Similarly, we can show that
∠E = 90° – \(\frac {∠B}{2}\)
and ∠F = 90°- \(\frac {∠C}{2}\)
![]()
Question 9.
Two congruent circles intersect each other at point A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Solution:
Given: Two congruent circles intersect each other at point A and B. A line through A meets the circles in P and Q.
To Prove: BP = BQ
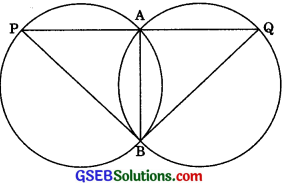
Proof: AB is the common chord of the two congruent circles.
∴ ∠APB = ∠AQB
[∴ Angles subtended by equal chords are equal]
∴ BP = BQ
[Sides opposite to equal angles are equal]
Question 10.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Solution:
Given: Bisector AP of angle A of ΔABC and the perpendicular bisector PQ of its opposite side BC intersect at P.
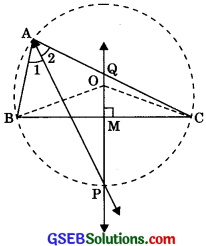
To prove: P lies on the circumcircle of the triangle ABC, i.e., P, A, B and C are concyclic
Construction: Draw the circle through three non-collinear points A, B and C with centre O on PQ.
Proof: ∠BAP = ∠CAP = \(\frac {∠BA}{2}\)
[∴ AP is the bisector of ∠BAC]
In ΔBMO and ΔCMO,
BM = CM [Given]
BO = CO [radii]
MO = MO [Common]
ΔBMO = ΔCMO [SSSI]
∠BOM = ∠COM [CPCT]
⇒ ∠BOP = ∠COP = \(\frac {∠BOC}{2}\) ………….(1)
Also, ∠BAC = \(\frac {∠BOC}{2}\)
⇒ 2∠BAP = ∠BOP
∴∠BAP = \(\frac {∠BOC}{2}\)
⇒ It is only possible when P lies on the circle passing through A, B, C.
![]()