Gujarat Board GSEB Solutions Class 9 Maths Chapter 12 Heron’s Formula Ex 12.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 12 Heron’s Formula Ex 12.1
Question 1.
A traffic signal board, indicating ‘SCHOOL AHEAD’ is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
Solution:
According to the question, semi-perimeter of ΔABC
s = \(\frac {a + a + a}{2}\) = \(\frac {3a}{2}\)
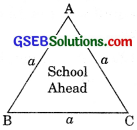
∴ Area of the signal board ABC

Now perimeter of this triangle = 180 cm
3a = 180
a = 60cm
Area of the signal board = \(\frac{\sqrt{3}}{4}\) (60)2
= \(\frac {3600}{2}\)\(\sqrt{3}\) = 900\(\sqrt{3}\) cm2
Aliter,
s = \(\frac {3a}{2}\) = \(\frac {3}{2}\) x 60 = 90 cm
Area = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{90(90-60)(90-60)(90-60)}\)
= \(\sqrt{90 \times 30 \times 30 \times 30}\)
= \(\sqrt{3 \times 30 \times 30 \times 30 \times 30}\)
= 900\(\sqrt{3}\) cm2.
![]()
Question 2.
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m. The advertisements yield an earning of ₹ 5000 per m2 per year. A company hired one of its walls for 3 months. How much rent did it pay?
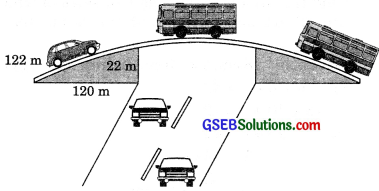
Given a = 122 m, b = 22m, c = 120m.
s = \(\frac {a + a + a}{2}\)
= \(\frac {122 + 22 + 120}{2}\) = 132 m
Area of the wall
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{132(132-122)(132-22)(132-120)}\)
= \(\sqrt{132 \times 10 \times 110 \times 12}\)
= \(\sqrt{11 \times 12 \times 10 \times 11 \times 10 \times 12}\)
= 12 x 11 x 10 = 1320 m2.
Rent paid by company for 3 months the rate of ₹ 5000/m2/year
= ₹ \(\frac{5000 \times 3 \times 1320}{12}\) = ₹ 16,50,000.
![]()
Question 3.
There is a slide in a park. One of its side walls has been painted in some color with a message “KEEP THE PARK GREEN AND CLEAN”. If the sides of the wall are 15 m, 11 m, and 6 m, find the area painted in color.
Given, a = 15m, b = 11 m, c = 6m.
s = \(\frac {a + a + a}{2}\)
s = \(\frac {15 + 11 + 6}{2}\) = 16 m
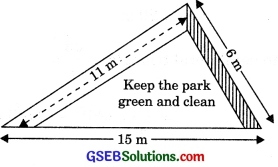
∴ Area painted in colour
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{16(16-15)(16-11)(16-6)}\)
= ,\(\sqrt{16 \times 1 \times 5 \times 10}\)
= \(\sqrt{4 \times 4 \times 5 \times 5 \times 2}\)
= 20\(\sqrt{2}\) m2
![]()
Question 4.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Solution:
Given, a = 18 cm, b = 10 cm, perimeter =42 cm.
a + b + c = 42
18 + 10 + c = 42
28 + c = 42
c = 14cm
s = \(\frac {42}{2}\) = 21 cm.
∴ Area of the triangle
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{21(21-18)(21-10)(21-14)}\)
= \(\sqrt{21 \times 3 \times 11 \times 7}\)
= \(\sqrt{7 \times 3 \times 3 \times 11 \times 7}\)
= 21 \(\sqrt{11}\) cm2
Question 5.
Sides of a triangle are in the ratio of 12: 17 : 25 and its perimeter is 540 cm. Find its area.
Solution:
Let the sides of a triangle be 12x cm, 17x cm and 25x cm.
Perimeter = 12x + 17x + 25x = 54x cm
54x = 540
x = 10
∴ Sidesare a = 12 x 10 = 120cm
b = 17 x 10 = 170 cm
c = 25 x 10 = 250cm
s = \(\frac {a + a + a}{2}\) = \(\frac {540}{2}\) = 270 m
∴ Area of the triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{270(270-120)(270-170)(270-250)}\)
= \(\sqrt{270 \times 150 \times 100 \times 20}\)
= \(\sqrt{9 \times 30 \times 5 \times 30 \times 5 \times 20 \times 20}\)
= 3 x 30 x 5 x 20 = 9000 cm2.
![]()
Question 6.
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Solution:
Given, a = 12 cm, b = 12 cm, Perimeter = 30 cm
a + b + c = 30
12 + 12 + c = 30
c = 30 – 24 = 6cm
s = \(\frac {30}{2}\) = 15cm
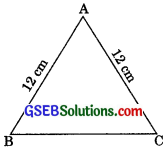
∴ Area of the triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{15(15-12)(15-12)(15-6)}\)
= \(\sqrt{15 \times 3 \times 3 \times 9}\) = 9\(\sqrt{15 }\)cm2
![]()