Gujarat Board GSEB Solutions Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.2
Question 1.
In figure, ABCD is a parallelogram, AE ⊥ DC andCF AD ⊥ AB = 16cm,AE = 8 cm and CF = 10 cm, find AD.
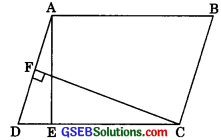
Solution:
ar( || gm ABCD) = AB x AE = 16 x 8 cm2
= 128 cm2 ………..(1)
ar( || gm ABCD) = AD x CF
= AD x 10 cm2 ……….(2)
From (1) and (2), we get
AD x 10 = 128
AD = \(\frac {128}{10}\)
AD = 12.8 cm.
![]()
Question 2.
If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH) = \(\frac {1}{2}\)ar (ABCD).
OR
Prove that the area of the quadrilateral formed by joining the mid-points of the sides of a parallelogram is half the area of the parallelogram.
Solution:
Given: A parallelogram ABCD, in which E, F, G, and H are the mid-points of sides AB, BC, CD, and DA respectively.
To prove: ar (EFGH) = ar(ABCD)
Construction: Join HF.
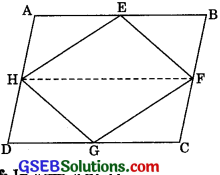
Proof: In || gm ABCD,
AD || BC and AD = BC (Opposite sides of a || gm)
⇒ \(\frac {1}{2}\) AD || \(\frac {1}{2}\)BC and \(\frac {1}{2}\) AD = \(\frac {1}{2}\)BC
⇒ AH || BF and AH = BF
∴ ABFH is a parallelogram.
(If a pair of opposite side of a quadrilateral is parallel and equal, it is a parallelogram)
Further, ΔEFH and ||gm ABFH lie between same base FH and between same parallels AB and FH.
∴ ar(ΔEFH) = \(\frac {1}{2}\) ar( || gm ABFH) ……….(1)
Similarly, we can show
ar(ΔFGH) = \(\frac {1}{2}\) ar(|| gm FCDH) ………..(2)
Adding eqn. (1) and (2), we get
ar(ΔEFH) + ar(ΔFGH)
= \(\frac {1}{2}\) ar(||gm ABFH) + \(\frac {1}{2}\) ar(||gmFCD)
∴ ar(EFGH) =\(\frac {1}{2}\) [ar(ABFH) + ar(FCDH)]
= \(\frac {1}{2}\) ar(ABCD).
![]()
Question 3.
P and Q are any two points lying on the sic DC and AD respectively of a parallelogram ABCD. Show that ar(ΔAPB) = ar(ΔBQC).
Solution:
APB and || gm ABCD are on the same AB and between the same parallels AB and DC.
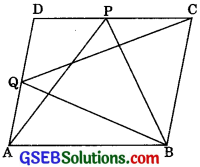
∴ ar(ΔAPB) = \(\frac {1}{2}\) ar( || gm ABCD) ………..(1)
Again, ABQC and 11gm ABCD are on the same base BC and between the same parallels BC and AD.
∴ ar(BQC) = \(\frac {1}{2}\) ar( || gm ABCD) ………(2)
From (1) and (2),
ar[ΔAPB] = ar[ΔBQC]
Question 4.
In figure, P is a point in the interior of a parallelogram ABCD. Show that:
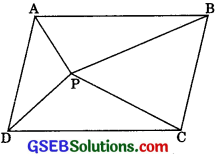
1. ar(ΔAPB) + ar(ΔPCD) = ar( || gm ABCD)
2. ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD)
[Hint: Through P, draw a line parallel to AB]
Solution:
Construction: Through P, draw a line EF parallel to AB.
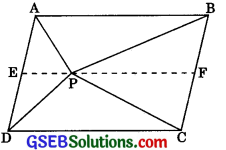
1. EF fi AB …….(1) (by construction)
∴ AD || BC
∴ Opposite sides of a parallelogram are parallel
∴ AE || BF ………..(2)
In view of (1) and (2),
Quadrilateral ABEF is a parallelogram.
A quadrilateral is a parallelogram if its opposite sides are parallel
Similarly, quadrilateral CDEF is a parallelogram.
∴ ΔAPB and fi gm ABFE are on the same base AB and between the same parallels AB and EF.
∴ ar(ΔAPB) = \(\frac {1}{2}\) ar(|| gm ABFE) …….(3)
Again, LSPCÐ and fi gin CDEF are on the same base DC and between the same parallels DC and EF.
∴ ar(ΔPCD) = \(\frac {1}{2}\) ar(|| gm CDEF) ………..(4)
Adding (3) and (4), we get
\(\frac {1}{2}\) ar(ΔAPB) + \(\frac {1}{2}\) ar(ΔPCD)
= \(\frac {1}{2}\) ar(|| gm ABFE) + \(\frac {1}{2}\) ar(|| gm in CDEF)
= \(\frac {1}{2}\) [ar(|| gm ABFE) + ar(|| gm CDEF)
= \(\frac {1}{2}\) ar(|| gm ABCD) ……….(5)
![]()
2. ar(ΔAPD) + ar(ΔPBC)
= ar( || gm ABCD) – [arΔAPB) + ar(ΔPCD)]
= 2[ar(ΔAPB) + ar(ΔPCB)] – [ar(ΔAPB) + ar(ΔPCD)]
= ar(ΔPB) + ar(ΔPCD).
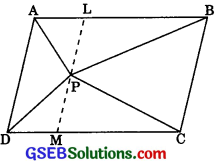
Alternative: Like in part (i), draw a line ∠M, through P, parallel to AD. Hence we can show
ar(ΔAPD) + ar(ΔPBC)
= ar(|| gm ABCD)
From eqn. (5) and (6),
ar(ΔAPD) + ar(ΔPBC)
= \(\frac {1}{2}\) ar(ΔAPB) + ar(ΔPCD)
Question 5.
In figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that:
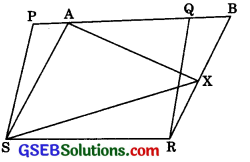
1. ar( || gm PQRS) = ar( || gm ABRS)
2. ar(ΔAXS) = \(\frac {1}{2}\) ar(|| gm PQRS)
Solution:
1. In ΔPSA and ΔQRB,
∠SPA = ∠RQB
Corresponding angles as PS || QR and transversal PB
∠PAS = ∠QBR
Corresponding angles from AS || BR and transversal PB
![]()
Also, PS = QR
[Opposite sides of || gm PQRS
ΔPSA = ΔQRB [By AAS rule]
∴ ar(ΔPSA) = ar(ΔQRB) ………..(1)
[∴ congruent figures have equal areas]
Now, ar(|| gm PQRS)
= ar(ΔPSA) + \(\frac {1}{2}\) ar(||gm AQRS)
= ar(ΔQRB) + \(\frac {1}{2}\) ar(||gm AQRS) [ using (1) ]
= ar(|| gm ABRS) …….(2)
2. ΔAXS and || gm ABRS are on the same base AS and between the same parallels AS and BR.
∴ ar(ΔAXS) = \(\frac {1}{2}\) ar( || gm ABRS)
= \(\frac {1}{2}\) ar( || gm PQRS) [(Using(2))]
![]()
Question 6.
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
Solution:
∴ ΔAPQ, ΔAPS, and ΔAQR lie between the same parallels.
∴ Their attitudes are the same. Let it be x. Then,

∴ SR = PQ (opposite sides of the parallelogram are equal)
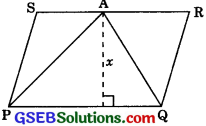
From eqn. (1) and (2),
ar(ΔAPQ) = ar(ΔAPS) + ar(ΔAQR)
Therefore, either the former should sow wheat in ΔAPQ and pulses in the other two triangles APS and AQR or pulses in ΔAPQ and wheat in the other two triangles APS and AQR.
![]()