GSEB Solutions Class 9 Science Chapter 11 કાર્ય અને ઊર્જા

Gujarat Board GSEB Solutions Class 9 Science Chapter 11 કાર્ય અને ઊર્જા Textbook Questions and Answers, Intext Questions, Textbook Activites Pdf.

કાર્ય અને ઊર્જા Class 9 GSEB Solutions Science Chapter 11

GSEB Class 9 Science કાર્ય અને ઊર્જા Textbook Questions and Answers

સ્વાધ્યાયના પ્રશ્નોત્તર

પ્રશ્ન 1.
નીચેની યાદીમાં દર્શાવેલ પ્રવૃત્તિઓ જુઓ. તમારી કાર્ય શબ્દની સમજને આધારે વિચારો કે તેમાં કાર્ય થઈ રહ્યું છે કે નહિ?

(i) સુમા એક તળાવમાં તરી રહી છે.
ઉત્તર:
હા. સૂમાં કાર્ય કરે છે. સ્મા પોતાના હાથ અને પગ વડે બળ લગાડીને પાણીને પાછળ તરફ ધકેલે છે અને પોતે આગળની દિશામાં સ્થાનાંતર કરે છે.

(ii) એક ગધેડાએ પોતાની પીઠ પર બોજ (ભાર) ઉઠાવેલ છે.
ઉત્તર:
ના. ગધેડા દ્વારા થયેલ કાર્ય શૂન્ય છે. ગધેડો ચાલતો હોય, તો બોજ(ભાર)નું સ્થાનાંતર સમક્ષિતિજ દિશામાં છે અને તેના દ્વારા બોજ (ભાર) પર લગાડાતું બળ ઊર્ધ્વદિશામાં છે અર્થાત્ બોજ(ભાર)નું સ્થાનાંતર અને બળ બને પરસ્પર લંબરૂપે છે.
પણ ચાલતી વખતે ગધેડો જમીન વડે લાગતા ઘર્ષણબળ અને હવાના અવરોધક બળ વિરુદ્ધ કાર્ય કરે છે.

(iii) એક પવનચક્કી કૂવામાંથી પાણી ખેંચી રહી છે.
ઉત્તર:
હા. પવનચક્કી કૂવામાંથી પાણી ખેંચતી વખતે પૃથ્વીના ગુરુત્વાકર્ષણ બળ વિરુદ્ધ કાર્ય કરે છે.

(iv) એક લીલા છોડમાં પ્રકાશસંશ્લેષણની ક્રિયા થઈ રહી છે. હું
ઉત્તર:
ના. પ્રકાશસંશ્લેષણની ક્રિયા દરમિયાન લીલા છોડનાં પાંદડાં સ્થિર રહે છે. તેથી તેમનું સ્થાનાંતર શૂન્ય છે અને બળ પણ ગેરહાજર છે. તેથી કાર્ય થતું નથી.

(v) એક એન્જિન ટ્રેન(રેલગાડી)ને ખેંચી રહ્યું છે.
ઉત્તર:
હા. એન્જિન વડે લાગતા ખેંચાણ બળ અને ટ્રેનના ડબ્બાઓનું સ્થાનાંતર એક જ દિશામાં છે.

(vi) સૂર્યના તડકામાં અનાજના દાણા સુકાઈ રહ્યા છે.
ઉત્તર:
(vi)
(vii) સઢવાળી એક હોડી પવન-ઊર્જાને કારણે ગતિશીલ છે.
ઉત્તર:
હા. પવનને લીધે સઢવાળી હોડી પર બળ લાગે છે અને – તેનું સ્થાનાંતર પણ બળની દિશામાં થાય છે.

પ્રશ્ન 2.
એક પદાર્થને જમીનથી કોઈ ચોક્કસ ખૂણે ફેંકવામાં આવે : છે. તે એક વક્રમાર્ગ પર ભ્રમણ કરીને પાછી જમીન પર આવીને પડે – છે. પદાર્થના માર્ગનું પ્રારંભિક અને અંતિમ બિંદુ એક જ સમક્ષિતિજ : રેખા પર સ્થિર છે. પદાર્થ પર ગુરુત્વબળ દ્વારા કેટલું કાર્ય થયું હશે?
ઉત્તરઃ
પદાર્થના ગતિમાર્ગનું પ્રારંભિક સ્થાન અને અંતિમ સ્થાન જમીન પરની સમક્ષિતિજ રેખા પર છે. તેથી પદાર્થનું સ્થાનાંતર સમક્ષિતિજ દિશામાં થાય છે. પણ તેના પર લાગતું ગુરુત્વાકર્ષણ બળ શિરોલંબ અધોદિશામાં છે. તેથી પદાર્થ પર ગુરુત્વબળ દ્વારા થતું કાર્ય શૂન્ય છે.

પ્રશ્ન 3.
એક બૅટરી એક વિદ્યુત ગોળા(બલ્બ)ને પ્રકાશે છે. આ પ્રક્રિયામાં થતા ઊર્જા-રૂપાંતરણોનું વર્ણન કરો. [2 ગુણ)
ઉત્તર:
સૌપ્રથમ બૅટરી રાસાયણિક ઊર્જાનું રૂપાંતરણ વિદ્યુતઊર્જામાં કરે છે. પછી આ વિદ્યુત-ઊર્જાના ભોગે ઉષ્મા-ઊર્જા અને પ્રકાશ-ઊર્જા બલ્બમાં ઉદ્ભવે છે.

∴ આપેલ પ્રક્રિયામાં ઊર્જાના રૂપાંતરણની શ્રેણી નીચે મુજબ છે :
રાસાયણિક ઊર્જા → વિદ્યુત-ઊર્જા → ઉષ્મા-ઊર્જા અને પ્રકાશઊર્જા

પ્રશ્ન 4.
20 kg દળનો પદાર્થ તેના પર લાગતા કોઈ બળને લીધે તેના વેગમાં 5 m s^-1 થી 2 m s^-1 જેટલો ફેરફાર અનુભવે છે. બળ દ્વારા થતાં કાર્યની ગણતરી કરો.
ઉકેલ:
અહીં, m = 20 kg; u = 5 m s^-1; = 2 m s^-1 W = ?
લાગતાં બળને લીધે થતું કાર્ય,
W = ગતિ-ઊર્જામાં થતો ફેરફાર
= (અંતિમ ગતિ-ઊર્જા) – (પ્રારંભિક ગતિ-ઊર્જા)
= \(\frac{1}{2}\) mv² – mu²
= \(\frac{1}{2}\) m (v² – u²)
= \(\frac{1}{2}\) × 20 (2² – 5²)
= 10 × (4 – 25) = 10 × (21) = – 210
અત્રે, પદાર્થ પર લાગતાં બળ વડે થતું કાર્ય 210 J છે.
ઋણ નિશાની સૂચવે છે કે પદાર્થ પર લાગતા બળનો પ્રકાર અવરોધક બળ છે, અર્થાત્ લાગતું બળ મંદક બળ (retarding force) છે.

પ્રશ્ન 5.
10 kg દળનો પદાર્થ ટેબલ પર A બિંદુ પર રાખેલ છે. તેને B બિંદુ સુધી લઈ જવામાં આવે છે. જો A અને Bને જોડતી રેખા સમક્ષિતિજ હોય, તો પદાર્થ પર ગુરુત્વબળ દ્વારા થતું કાર્ય કેટલું ? હશે? તમારો ઉત્તર વર્ણવો.
ઉકેલ:

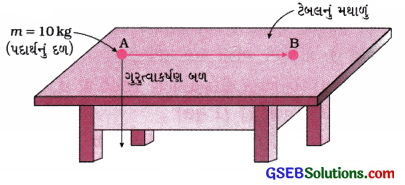
અહીં, પદાર્થનું સ્થાનાંતર AB સમક્ષિતિજ દિશામાં છે. ગતિ છે દરમિયાન તેની ઊંચાઈમાં કોઈ જ ફેરફાર થતો નથી. ∴ h = 0 પદાર્થ પર લાગતું ગુરુત્વાકર્ષણ બળ શિરોલંબ અધોદિશામાં છે. (અર્થાત્ બળ ⊥ સ્થાનાંતર).
હવે, ગુરુત્વાકર્ષણ બળ વડે થતું કાર્ય W = mgh = mg × 0 = 0
આમ, અત્રે પદાર્થ પર ગુરુત્વાકર્ષણ બળ દ્વારા થતું કાર્ય શૂન્ય છે.

પ્રશ્ન 6.
મુક્ત પતન કરતા પદાર્થની સ્થિતિ-ઊર્જા સતત ઘટતી જાય છે. શું તે ઊર્જા-સંરક્ષણના નિયમનું ઉલ્લંઘન કરે છે? કારણ જણાવો.
ઉત્તર:
મુક્ત પતન કરતા પદાર્થની સ્થિતિ-ઊર્જા (E_p) ક્રમિક (progressively) ઘટે છે. પદાર્થ શિરોલંબ અધોદિશામાં ગતિ કરે છે. તેથી તેનો વેગ ક્રમિક વધે છે. પરિણામે તેની ગતિ-ઊર્જા (E_k) ક્રમિક રીતે વધે.
∴ ગતિપથ પરના દરેક બિંદુ આગળ કુલ યાંત્રિક ઊર્જા (E_p + E_k) અચળ રહે છે.
∴ ઊર્જા સંરક્ષણના નિયમનું ઉલ્લંઘન થતું નથી.

પ્રશ્ન 7.
જ્યારે તમે સાઇકલ ચલાવો છો ત્યારે કઈ કઈ ઊર્જાઓ : રૂપાંતરિત થાય છે?
ઉત્તર:
સૌપ્રથમ આપણે લીધેલા ખોરાકની આંતરિક ઊર્જા રાસાયણિક ઊર્જા સ્નાયુ-શક્તિમાં રૂપાંતરિત થાય છે.

જ્યારે આપણે સાઇકલનું પેડલ લગાડીએ છીએ ત્યારે આપણી સ્નાયુ-શક્તિ સાઇકલની ગતિ-ઊર્જામાં રૂપાંતરિત થાય છે, જેના લીધે સાઇકલ ચાલે છે. તદ્દુપરાંત થોડી સ્નાયુ-શક્તિ રસ્તા વડે સાઇકલના ટાયર પર લાગતાં ઘર્ષણબળ વિરુદ્ધ ગતિ કરવામાં પણ વપરાય છે. તેથી થોડીક સ્નાયુ-શક્તિ ઉષ્મા-ઊર્જારૂપે પણ વિખેરણ પામે છે.

પ્રશ્ન 8.
જ્યારે તમે તમારી બધી જ તાકાત લગાડીને એક મોટા પથ્થરને ધકેલવાનો પ્રયત્ન કરો છો, પરંતુ તેને ધકેલવામાં નિષ્ફળ થઈ જાઓ છો. શું આ અવસ્થામાં ઊર્જાનું રૂપાંતરણ થાય છે ખરું? તમારા દ્વારા વપરાયેલી ઊર્જા ક્યાં જાય છે?
ઉત્તર:
હા. જ્યારે આપણે મોટા પથ્થરને ધકેલવા માટે તેના પર – મોટું બળ લગાડીએ છીએ ત્યારે તે બળ વડે કાર્ય ત્યારે જ થયું કહેવાય કે જ્યારે પથ્થરનું સ્થાનાંતર થાય. પણ અહીં પથ્થરનું સ્થાનાંતર થતું નથી. તેથી તેના પર કાર્ય થતું નથી.
પણ આપણે થાકી જઈએ છીએ, કારણ કે આપણી સ્નાયુ-શક્તિ સ્નાયુતંતુઓનું વિસ્તરણ અને સંકોચન કરવામાં ખર્ચાઈ જાય છે; જે ઉષ્મા-ઊર્જામાં રૂપાંતરિત થાય છે.

પ્રશ્ન 9.
એક ઘરમાં એક મહિનામાં 250 ‘યુનિટ’ ઊર્જા વપરાય છે. આ ઊર્જા જૂલ એકમમાં કેટલી થશે?
ઉકેલ:
1 યુનિટ (વિદ્યુત) ઊર્જા = 1 kWh = 3.6 × 10⁶ J .
250 યુનિટ ઊર્જા = 250 × 3.6 × 10⁶ J
= 900 × 10⁶ J = 9 × 10⁸ /j

પ્રશ્ન 10.
40 kg દળના પદાર્થને જમીનથી 5 mની ઊંચાઈ પર લઈ જવામાં આવે છે. તેની સ્થિતિ-ઊર્જા કેટલી થાય? જો આ પદાર્થને મુક્ત પતન કરવા દેવામાં આવે અને તે જ્યારે અડધા રસ્તે પહોંચે ત્યારે તેની ગતિ-ઊર્જાની ગણતરી કરો. (g = 10 m s^-2
ઉકેલ:
અહીં, m = 40 kg; h = 5 m; g = 10 m s^{– 2}; u = 0
સ્થિતિ-ઊર્જા E_p = mgh
= 40 × 10 × 5 = 2000 J …….. (1)
જ્યારે આ પદાર્થને મુક્ત પતન કરવા દેવામાં આવે ત્યારે તેની સ્થિતિ-ઊર્જા ગતિ-ઊર્જામાં ફેરવાય છે. જ્યારે પદાર્થ નીચે તરફ અડધી ઊંચાઈએ હોય ત્યારે અધોદિશામાં તેણે કાપેલું અંતર = h = 2.5 m થાય.
ધારો કે, આ સ્થાને પદાર્થનો વેગ છે, તો
v² – u² = 2 as પરથી,
v² – u² = 2gh
⇒ v² – 0² = 2 × 10 × 2.5
∴ v² = 50 (m/s)²
∴ ગતિ-ઊર્જા E_k = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) × 40 × 50 = 1000 J …….. (2)

બીજી રીતઃ મુક્ત પતન કરતો પદાર્થ જ્યારે અડધી ઊંચાઈએ પહોંચે ત્યારે, જમીનથી તેની ઊંચાઈ h’ = 2.5 m થાય.
આ સ્થાને તેની સ્થિતિ-ઊર્જા = mgh’
= 40 × 10 × 2.5
= 1000 J
પણ મુક્ત પતન કરતા પદાર્થની યાંત્રિક ઊર્જાનું હંમેશાં સંરક્ષણ થાય છે.
∴ h ઊંચાઈએ પદાર્થની યાંત્રિક ઊર્જા = \(\frac{h}{2}\) ઊંચાઈએ પદાર્થની યાંત્રિક ઊર્જા .
∴ mgh + 0 = mgh’ + E_k (∵ મુક્ત પતન કરતા પદાર્થની પ્રારંભિક ગતિ-ઊર્જા = 0)
∴ 2000 J = 1000 J + E_k
∴ E_k = 2000 – 1000
= 1000 J

પ્રશ્ન 11.
પૃથ્વીની ચારે બાજુ ફરતાં કોઈ ઉપગ્રહ પર ગુરુત્વબળ દ્વારા કેટલું કાર્ય થશે? તમારો જવાબ તર્કસંગત રીતે આપો.
ઉત્તર:
શૂન્ય.

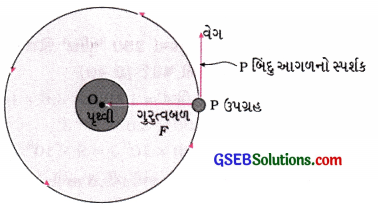
[આકૃતિ 11.16]

જ્યારે ઉપગ્રહ પૃથ્વીની આસપાસ વર્તુળાકાર કક્ષામાં પરિક્રમણ કરે છે ત્યારે આપેલ બિંદુ (ધારો કે P) પાસે અતિ સૂક્ષ્મ સમયગાળામાં તેનું સ્થાનાંતર s, ત્યાં દોરેલા સ્પર્શકની દિશામાં હોય છે; પણ ઉપગ્રહ પર લાગતું પૃથ્વીનું ગુરુત્વાકર્ષણ બળ ત્રિજ્યાવર્તી દિશામાં કેન્દ્રગામી હોય છે. (જુઓ આકૃતિ 11.16)

હવે, વર્તુળપથના આપેલ બિંદુ પાસેનો સ્પર્શક હંમેશાં તે બિંદુ પાસે ત્રિજ્યાને લંબરૂપે હોય છે. તેથી ગુરુત્વબળ F, સ્થાનાંતર ને લંબરૂપે છે, જે દર્શાવે છે કે ઉપગ્રહનું સ્થાનાંતર s, ગુરુત્વબળ Fની દિશામાં થતું નથી. તેથી સ્થાનાંતર s = 0
∴ ગુરુત્વબળ દ્વારા થયેલું કાર્ય W = F × s = F × 0 = 0

પ્રશ્ન 12.
શું કોઈ પદાર્થ પર લાગતાં બળની ગેરહાજરીમાં તેનું સ્થાનાંતર થશે? વિચારો. આ પ્રશ્નની બાબતમાં તમારા મિત્રો તથા શિક્ષકો સાથે વિચાર-વિમર્શ કરો.
ઉત્તર:
હા.
પદાર્થ પર બળ લાગતું ન હોય, તો F = 0. તેથી ન્યૂટનના ગતિના બીજા નિયમ F = ma પરથી,
0 = ma
પણ m ≠ 0
∴ a = 0
આવા કિસ્સામાં પદાર્થ સ્થિર અવસ્થામાં હોય, તો સ્થિર રહેશે અને જો સુરેખ પથ પર નિયમિત ગતિ કરતો હોય, તો તે પોતાની ગતિ ચાલુ રાખશે (ન્યૂટનનો ગતિનો પ્રથમ નિયમ).
તેથી ઉપરોક્ત બીજી પરિસ્થિતિમાં પદાર્થનું સ્થાનાંતર થાય છે, પણ બળ ગેરહાજર છે.
ટૂંકમાં, ન્યૂટનના ગતિના પ્રથમ નિયમ અનુસાર પદાર્થ પર બળ લાગતું ન હોય, તો પદાર્થ પોતાની ગતિ અચળ વેગ(સદિશ)થી ચાલુ રાખે છે.

પ્રશ્ન 13.
કોઈ વ્યક્તિ ભૂસાથી ભરેલ ગાંસડીને પોતાના માથા પર 30 મિનિટ સુધી રાખે છે. પછી થાકી જાય છે. શું તેણે કોઈ કાર્ય કર્યું કહેવાય? તમારા જવાબનું વ્યાજબીપણું ચકાસો.
ઉત્તર:
ના. તે વ્યક્તિએ કાર્ય કર્યું કહેવાય નહીં.
કારણ કે અહીં વ્યક્તિ ગાંસડીને પોતાની સ્નાયુ-શક્તિના ઉપયોગથી ઊંચકે છે, એટલે કે બળ લગાડે છે, પણ ગાંસડીનું સ્થાનાંતર થતું નથી. અર્થાત્ = 0. તેથી વ્યક્તિ વડે થતું કાર્ય W = F × 0 = 0.
વ્યક્તિ ગાંસડી ઊંચકવા માટે પોતાની સ્નાયુ-શક્તિ વાપરે છે તે વખતે સ્નાયુઓ ખેંચાય છે અને સંકોચાય પણ છે. તેથી ઉષ્મા-ઊર્જા ઉભવે છે. પરિણામે વ્યક્તિ થાકી જાય છે.

પ્રશ્ન 14.
એક વિદ્યુત હીટરનો પાવર 1500 જ છે. 10 કલાકમાં તે કેટલી ઊર્જા વાપરશે?
ઉકેલ:
અહીં, P = 1500 W; t = 10 h
ઊર્જા = પાવર × સમય
= 1500 W × 10 h
= 1.5 kW × 10 h = 15 kWh = 15 unit

પ્રશ્ન 15.
જ્યારે આપણે કોઈ સાદા લોલકને એક છેડે લઈ જઈને છોડી દઈએ છીએ તો તે દોલન કરે છે. આ ઘટનામાં થતાં ઊર્જાનાં રૂપાંતરણોની ચર્ચા કરો અને તે પરથી ઊર્જા-સંરક્ષણના નિયમને સ્પષ્ટ કરો.
લોલક થોડા સમય બાદ સ્થિર અવસ્થામાં કેમ આવી જાય છે? આ સ્થિતિમાં તેની ઊર્જાનું શું થાય છે? શું તે ઊર્જા-સંરક્ષણના નિયમનું ઉલ્લંઘન કરે છે? [4 ગુણ)
ઉત્તર:

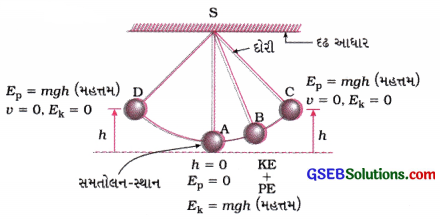
[આકૃતિ 11.17].

અવગણ્ય દળવાળી દોરીના છેડે લટકતી અને એક જ ઊર્ધ્વતલમાં દોલિત થતા નાના દળદાર પદાર્થની રચનાને સાદું લોલક કહે છે.
આકૃતિ 11.17માં બતાવ્યા પ્રમાણે A સાદા લોલકનું સમતોલન સ્થાન – મધ્યમાન સ્થાન છે.
હવે, જ્યારે સાદા લોલકના ગોળાને C બિંદુ સુધી સ્થાનાંતરિત કરવામાં આવે છે ત્યારે તે ગુરુત્વીય સ્થિતિ-ઊર્જા મેળવે છે. C બિંદુ પાસે તેની ગુરુત્વીય સ્થિતિ-ઊર્જા મહત્તમ E_p = mgh જેટલી છે અને તેનો વેગ ત્યાં શૂન્ય હોવાથી ગતિ-ઊર્જા E_k = 0 છે.
C બિંદુ આગળથી ગોળાને મુક્ત કરતાં તે મધ્યમાન સ્થાન A તરફ ગતિ કરવા લાગે છે. તે વખતે તેનો વેગ વધવા લાગે છે. પરિણામે તેની ગતિ-ઊર્જા વધે છે અને ઊંચાઈ ઘટવાથી સ્થિતિ-ઊર્જા ઘટે છે.

ગતિપથના વચગાળાના B સ્થાને તેની ઊર્જા અંશતઃ સ્થિતિઊર્જા અને ગતિ-ઊર્જારૂપે હોય છે.
મધ્યમાન સ્થાને તેની ઊર્જા સંપૂર્ણપણે ગતિ-ઊર્જારૂપે હોય છે, અર્થાત્ મહત્તમ હોય છે અને ત્યાં h = 0 હોવાથી સ્થિતિ-ઊર્જા E_p શૂન્ય હોય છે.
ગોળાની Aથી D તરફની ગતિ દરમિયાન તેની ગતિ-ઊર્જા ધીમે ધીમે સ્થિતિ-ઊર્જામાં રૂપાંતરિત થાય છે. તેથી ગતિ-ઊર્જા ઘટે છે અને ગોળાનો વેગ પણ ઘટે છે.
બિંદુ D પાસે ફરીથી તેની ઊર્જા સમગ્રતયા સ્થિતિ-ઊર્જારૂપે હોય છે અને ગતિ-ઊર્જા શૂન્ય હોય છે.

આમ, સાદું લોલક જ્યારે અંત્યબિંદુઓ C અને D વચ્ચે દોલન કરે છે ત્યારે સ્થિતિ-ઊર્જા અને ગતિ-ઊર્જા એકબીજામાં સતત રૂપાંતરિત થયા કરે છે, પણ તેમનો સરવાળો E_p + E_k અર્થાત્ કુલ યાંત્રિક ઊર્જા E તો અચળ જ રહે છે.
સાદા લોલકની ગતિ દરમિયાન તેની ઊર્જા, દઢ આધાર પાસે ઉદ્ભવતા ઘર્ષણબળ અને હવાના ઘર્ષણબળ વિરુદ્ધ ગતિ કરવામાં ખર્ચાય છે, જે ઉષ્મા-ઊર્જારૂપે વિખેરણ પામે છે. આમ, જેમ જેમ સમય પસાર થાય છે તેમ તેમ લોલકની ઊર્જા ઘટતી જાય છે અને અંતે શૂન્ય બને છે. તેથી સાદું લોલક સ્થિર અવસ્થામાં આવી જાય છે.
તેથી સ્પષ્ટ છે કે અહીં ઊર્જા સંરક્ષણના નિયમનું ઉલ્લંઘન થતું નથી.

પ્રશ્ન 16.
m દળ ધરાવતો પદાર્થ એક અચળ વેગ છથી ગતિમાન છે. પદાર્થો કેટલું કાર્ય કરવું જોઈએ કે જેથી તે સ્થિર સ્થિતિમાં આવી જાય?
ઉકેલ:
પદાર્થનું દળ = m, પદાર્થનો પ્રારંભિક વેગ = v, અંતિમ વેગ = 0
પદાર્થ પર થતું કાર્ય = પદાર્થની ગતિ-ઊર્જામાં થતો ફેરફાર
∴ W = (અંતિમ ગતિ-ઊર્જા) – (પ્રારંભિક ગતિ-ઊર્જા)
= \(\frac{1}{2}\)m(0)² – \(\frac{1}{2}\)mv² = – \(\frac{1}{2}\)mv ²
અહીં, પદાર્થ પર થતું કાર્ય –\(\frac{1}{2}\)mv²છે.
ઋણ નિશાની સૂચવે છે કે પદાર્થ પર કોઈ અવરોધક બળ લાગે છે. તેથી તેની ગતિ-ઊર્જા ઘટીને શૂન્ય બને છે.
અત્રે, પદાર્થ પોતાની ઊર્જા \(\frac{1}{2}\)mv² અવરોધક બળ વિરુદ્ધ વાપરીને અંતે સ્થિર સ્થિતિમાં આવે છે.
∴ પદાર્થે કરેલું કાર્ય = \(\frac{1}{2}\)mv²
નોંધઃ જો પદાર્થ પર અવરોધક બળ લાગતું ન હોય અને બાહ્ય અચળ બળ લાગતું હોય, તો તેની (અંતિમ ગતિ-ઊર્જા) > (પ્રારંભિક ગતિ-ઊર્જા) થાય.

પ્રશ્ન 17.
1500 kg દ્રવ્યમાનની કાર કે જે 60 km h^-1 ના વેગથી ગતિ કરી રહી છે. તેને રોકવા માટે કરવા પડતાં કાર્યની ગણતરી કરો.
ઉકેલ:
અહીં, દળ m = 1500 kg,
પ્રારંભિક વેગ u = 60 km h^-1 = 60 × \(\frac{5}{18}\) = \(\frac{50}{3}\) m s^-1,
અંતિમ વેગ v = 0
કારને રોકવા માટે કરવું પડતું કાર્ય = કારની ગતિ-ઊર્જામાં થતો ફેરફાર
∴ W = (અંતિમ ગતિ-ઊર્જા) – (પ્રારંભિક ગતિ-ઊર્જા)
= \(\frac{1}{2}\) × 1500 (0)² – \(\frac{1}{2}\) × 1500 × \(\left(\frac{50}{3}\right)^{2}\)
= – 208333.3 J
કાર પર થતું કાર્ય – 208333.34 છે.
ઋણ નિશાની સૂચવે છે કે કાર પર કોઈ અવરોધક બળ લાગે { છે. તેથી તેની ગતિ-ઊર્જા ઘટીને શૂન્ય બને છે.

પ્રશ્ન 18.
નીચે આપેલ દરેક સ્થિતિ માટે m દ્રવ્યમાનના એક પદાર્થ પર એક બળ લાગી રહ્યું છે. સ્થાનાંતરની દિશા પશ્ચિમથી પૂર્વ તરફ છે, જે એક લાંબા તીરથી દર્શાવેલ છે. આકૃતિ 11.18નાં ચિત્રોને ધ્યાનપૂર્વક જુઓ અને બતાવો કે દરેક કિસ્સામાં કરેલ કાર્ય ઋણ છે કે ધન છે કે શૂન્ય છે.

ઉકેલ:

1. કિસ્સા (a)માં પદાર્થ પર લાગતું બળ અને તેનું સ્થાનાંતર પરસ્પર લંબ છે. અહીં પદાર્થનું સ્થાનાંતર બળની દિશામાં થતું નથી. તેથી થતું કાર્ય W = 0.

2. કિસ્સા (b)માં પદાર્થ પર લાગતું બળ અને સ્થાનાંતર બંને એકસમાન દિશામાં છે. તેથી થતું કાર્ય ધન છે.

3. કિસ્સા (c)માં પદાર્થ પર લાગતું સ્થાનાંતર બળ સ્થાનાંતરની વિરુદ્ધ દિશામાં છે. તેથી આકૃતિ 11.19] થતું કાર્ય કણ છે.

પ્રશ્ન 19.
સોની કહે છે કે કોઈ પદાર્થનો પ્રવેગ શૂન્ય હોઈ શકે પછી ભલે તેના પર ઘણાં બધાં બળ કાર્ય કરી રહ્યાં હોય. શું તમે તેની સાથે સહમત છો? કેમ? [2 ગુણ].
ઉત્તર:
હા.
જ્યારે પદાર્થ પર લાગતાં ઘણાં બધાં બળોનું પરિણામી બળ F શૂન્ય હોય, તો તેનો પ્રવેગ વ શૂન્ય હોય છે.
a = \(\frac{F}{m}\) = \(\frac{0}{m}\) = 0

પ્રશ્ન 20.
દરેકનો પાવર 500 W હોય તેવાં ચાર સાધનો 10 કલાક માટે વાપરવામાં આવે છે, તો તેમના દ્વારા વપરાતી ઊર્જા kWhમાં શોધો.
ઉકેલ:
એક સાધનનો પાવર P = 500W = 0.5 kW, t = 10 h
∴ ચાર એકસરખાં સાધનો વડે વપરાતી કુલ ઊર્જા
= 4P × t
= 4 × 0.5 kW × 10 h
= 20 kWh
= 20 unit

પ્રશ્ન 21.
મુક્ત પતન કરતો એક પદાર્થ જમીન પર પડીને સ્થિર થાય છે, તો તેની ગતિ-ઊર્જાનું શું થશે?
ઉત્તર:
જ્યારે પદાર્થ મુક્ત પતન કરે છે ત્યારે તેની ગુરુત્વીય સ્થિતિ-ઊર્જા, ગતિ-ઊર્જામાં રૂપાંતરિત થાય છે. પદાર્થ જ્યારે જમીન પર પડીને સ્થિર થાય છે ત્યારે પદાર્થની ગતિ-ઊર્જા

• ઉષ્મા-ઊર્જામાં ફેરવાય છે.
• ધ્વનિ-ઊર્જામાં ફેરવાય છે.
• પદાર્થની સ્થિતિ-ઊર્જા (સંરચનાને લગતી) જમીનની સ્થિતિ-ઊર્જામાં ફેરવાય છે, કારણ કે પદાર્થમાં વિકૃતિ ઉદ્ભવે છે તથા જમીન થોડીક દબાઈ જાય છે.

GSEB Class 9 Science કાર્ય અને ઊર્જા Intext Questions and Answers

Intext પ્રશ્નોત્તર [પા.પુ. પાના નં. 148]

પ્રશ્ન 1.
કોઈ પદાર્થ ઉપર 7 Nનું બળ લાગે છે. માની લો કે બળની દિશામાં પદાર્થનું સ્થાનાંતર 8m છે (આકૃતિ 11.2). માની લો કે બળ પદાર્થના સમગ્ર સ્થાનાંતર દરમિય લાગી રહ્યું છે. આ સ્થિતિમાં કરેલું કાર્ય કેટલું હશે?

[આકૃતિ 11.2]
ઉકેલ:
અહીં, F = 7 N; s = 8 m; W = ?
કરેલું કાર્ય W = Fs
= 7 N × 8 m
= 56 N m
= 56 J

Intext પ્રશ્નોત્તર [પા.પુ. પાના નં. 149]

પ્રશ્ન 1.
આપણે ક્યારે કહીએ છીએ કે કાર્ય થયું છે?
ઉત્તર:
પદાર્થ પર કાર્ય થયું છે તેવું ત્યારે જ કહેવાય કે જ્યારે પદાર્થ પર બળ F લાગતું હોય અને તેના લીધે પદાર્થનું સ્થાનાંતર s થતું હોય.

પ્રશ્ન 2.
જ્યારે કોઈ પદાર્થ પર લગાવેલું બળ તેના સ્થાનાંતરની દિશામાં હોય, તો કરેલ કાર્યનું સૂત્ર લખો.
ઉત્તર:
કરેલું કાર્ય (W) = અચળ બળ (F) × સ્થાનાંતર (s)

પ્રશ્ન 3.
15 કાર્યને વ્યાખ્યાયિત કરો.
ઉત્તર:
પદાર્થ પર લાગતાં 1 N બળને લીધે પદાર્થનું સ્થાનાંતર બળની દિશામાં 1 m જેટલું થાય ત્યારે પદાર્થ પર થતું કાર્ય 1 J કહેવાય છે.

પ્રશ્ન 4.
બળદની એક જોડી ખેતર ખેડતી વખતે કોઈ હળ પર 140 N બળ લગાડે છે. ખેડાયેલ ખેતરની લંબાઈ 15 m છે. ખેતરને લંબાઈની દિશામાં ખેડવા માટે કેટલું કાર્ય કરવું પડશે?
ઉત્તર:
અત્રે બળ (F) = 140 N, સ્થાનાંતર (s) = 15 m, કાર્ય (W) = ?
W = (F) (s) = 140 N × 15 m = 2100 N m = 2100 J

Intext પ્રશ્નોત્તર [પા.પુ. પાના નં 152]

પ્રશ્ન 1.
પદાર્થની ગતિ-ઊર્જા એટલે શું?
ઉત્તરઃ
પદાર્થ પોતાની ગતિને કારણે કાર્ય કરવાની જે ક્ષમતા ધરાવે છે એટલે કે ઊર્જા ધરાવે છે, તેને પદાર્થની ગતિ-ઊર્જા કહે છે.

પ્રશ્ન 2.
પદાર્થની ગતિ-ઊર્જાનું સૂત્ર લખો.
ઉત્તરઃ
m દળ ધરાવતા તથા છ જેટલા સમાન વેગથી ગતિ કરતા પદાર્થની ગતિ-ઊર્જા,
E_k = \(\frac{1}{2}\)mv²

પ્રશ્ન 3.
5 ms^-1ના વેગથી ગતિ કરતા m દળના પદાર્થની ગતિઊર્જા 25 છે. જો વેગને બમણો કરી દેવામાં આવે, તો તેની ગતિ-ઊર્જા કેટલી થશે? જો વેગને ત્રણ ગણો કરવામાં આવે, તો ગતિ-ઊર્જા કેટલી થશે?
ઉત્તરઃ
અહીં, પ્રારંભમાં v = 5 m s^-1 અને E_k = 25 J
હવે, E_K = \(\frac{1}{2}\)mv²
∴ E_K ઇ v² (અહીં પદાર્થનું દળ m અચળ રહે છે.)
∴ E_K = (અચળાંક) v² …………… (1)

→ જ્યારે પદાર્થનો વેગ બમણો થાય ત્યારે તેની ગતિ-ઊર્જા,
E’_k = (અચળાંક) (2v)²
= 4 (અચળાંક) v² …………….. (2)
સમીકરણ (2) અને (1)નો ગુણોત્તર લેતાં,
\(\frac{E_{\mathrm{k}}^{\prime}}{E_{\mathrm{k}}}\) = 4
∴ E’_k = 4 E_k
= 4 × 25 J
= 100 J

→ જ્યારે પદાર્થનો વેગ ત્રણ ગણો થાય ત્યારે તેની ગતિ-ઊર્જા,
E”_k = (અચળાંક) (3v)²
= 9 (અચળાંક) v² ………… (3)
સમીકરણ (3) અને (1)નો ગુણોત્તર લેતાં,
\(\frac{E_{\mathrm{k}}^{\prime \prime}}{E_{\mathrm{k}}}\) = 9 .
∴ E”_k = 9
E_k = 9 × 25 J
= 225 J

Intext પ્રશ્નોત્તર [પા.પુ. પાના નં. 156]

પ્રશ્ન 1.
પાવર એટલે શું?
ઉત્તર:
એકમ સમયમાં થતા કાર્યને અથવા રૂપાંતરિત થતી ઊર્જાને પાવર કહે છે.

પ્રશ્ન 2.
1 w પાવર વ્યાખ્યાયિત કરો.
ઉત્તર:
જો કોઈ એજન્ટ (સાધન અથવા મશીન) 1 J કાર્ય 3 1 sમાં કરે, તો તેનો પાવર 1 W કહેવાય છે.

પ્રશ્ન 3.
એક બલ્બ 1000 1 વિદ્યુત-ઊર્જા 10 sમાં વાપરે છે. તેનો પાવર કેટલો હશે?
ઉત્તર:
અહીં, W = 1000 J; t = 10 s; P = ?

= \(\frac{1000 \mathrm{~J}}{10 \mathrm{~s}}\)
= 100 J S^-1
= 100 w

GSEB Class 9 Science કાર્ય અને ઊર્જા Textbook Activities

પ્રવૃત્તિ 11.1 [પા.પુ. પાના નં. 146 – 147]

રોજિંદા જીવનમાં આપણે કેટલીય પ્રવૃત્તિઓ કરીએ છીએ, જેને સામાન્ય રીતે કાર્ય માનવામાં આવે છે. આ દરેક પ્રવૃત્તિ માટે નીચે આપેલા પ્રશ્નો પૂછો અને તેના ઉત્તર આપોઃ

1. કયા પદાર્થ પર કાર્ય થયું?
2. પદાર્થ પર કઈ ક્રિયા થઈ?
3. કોણ (કયું) કાર્ય કરી રહ્યું છે?

ચર્ચા-વિચારણા: જુદી જુદી પ્રવૃત્તિઓને લગતા પ્રશ્નોના ઉત્તર:

1. જે પદાર્થ પર બળ લગાડવામાં આવે છે તે પદાર્થ પર કાર્ય થાય છે.
2. પદાર્થ પર બળ લાગવાને કારણે તે ગતિ કરે છે.
3. જે વ્યક્તિ અથવા agency, જેના વડે બળ લાગે છે તેના દ્વારા કાર્ય થાય છે.

નિષ્કર્ષ: રોજિંદા જીવનમાં થતી તે પ્રવૃત્તિઓ કે જેમાં પદાર્થ પર 5 બળ લાગતું હોય અને તે ગતિમાન થતો હોય ત્યારે કાર્ય થયું તેમ કહેવાય.

પ્રવૃત્તિ 11.2 [પા.પુ. પાના નં. 147]

• તમારા રોજિંદા જીવનની કેટલીક ઘટનાઓ પર વિચાર કરો કે જેમાં કાર્ય સમાયેલ હોય.
• તેની સૂચિ બનાવો.
• તમારા મિત્રો સાથે વિચાર-વિમર્શ કરો કે શું દરેક સ્થિતિમાં કાર્ય કરેલું છે?
• તમારા જવાબોનાં કારણો જાણવાનો પ્રયત્ન કરો.
• જો કાર્ય થયું છે, તો પદાર્થ ઉપર કયું બળ કાર્ય કરી રહ્યું છે?
• એ કયો પદાર્થ છે કે જેના પર કાર્ય થયું છે?
• જે પદાર્થ પર કાર્ય થયું છે, એની સ્થિતિમાં શું પરિવર્તન થાય છે?

ચર્ચા-વિચારણા:
→ સાઈકલ ચલાવવી, તરવું, રમતો રમવી, દાખલાઓ ગણવા વગેરે.
→ ઉપરની દરેક પરિસ્થિતિમાં કાર્ય થયેલું નથી. મતલબ દાખલા ગણવાની પ્રવૃત્તિ સિવાયની પ્રવૃત્તિઓમાં કાર્ય થયેલું છે.
→ કારણ કે, દાખલા ગણવાની પ્રવૃત્તિ સિવાયની પ્રવૃત્તિઓમાં બળ લાગે છે. જેના લીધે સ્થાનાંતર પણ થાય છે.
→ જે પ્રવૃત્તિમાં કાર્ય થયેલ છે તે પ્રવૃત્તિમાં વ્યક્તિના શરીર દ્વારા બળ લાગે છે અને પદાર્થનું સ્થાનાંતર થાય છે.
→ સાઇકલ ચલાવવાની પ્રવૃત્તિમાં સાઇકલ પર કાર્ય થાય છે અને સાઇકલ સ્થાનાંતરિત થાય છે.

નિષ્કર્ષ: આપેલ પદાર્થ પર કાર્ય થયું ત્યારે જ કહેવાય જ્યારે તેના પર બળ લાગતું હોય અને તેનું સ્થાનાંતર થતું હોય.

પ્રવૃત્તિ 11.3 [પા.પુ. પાના નં 147]

• એવી પરિસ્થિતિઓ પર વિચાર કરો કે જેમાં પદાર્થ પર બળ લગાડવા છતાં પણ તે સ્થાનાંતરિત થતો ન હોય અને એવી પરિસ્થિતિ ઉપર પણ વિચાર કરો, જ્યારે કોઈ પદાર્થ પર બળ લાગ્યા વિના તે સ્થાનાંતરિત થઈ જાય. દરેક માટે જેટલી પરિસ્થિતિઓ તમે વિચારી શકો તેની યાદી બનાવો.
• તમારા મિત્રો સાથે વિચાર-વિમર્શ કરો કે શું આ સ્થિતિમાં કાર્ય થયું છે ખરું?

ચર્ચા-વિચારણા:
→ પાટા પર ઊભેલા રેલવે એન્જિનને ધક્કો મારતાં (બળ લગાડતાં) તે જરાય ગતિ કરતું નથી.

આ કિસ્સામાં પદાર્થ પર બળ લાગે છે, છતાં પણ તેનું સ્થાનાંતર = થતું નથી. તેથી કાર્ય થતું નથી.
1. હવે જો રેલવે એન્જિન પોતાની અંદર રહેલા બળતણના દહનને લીધે ગતિમાં આવે, તો તે સ્થાનાંતરિત થાય છે.
પણ અહીં રેલવે એન્જિન પર કોઈ બાહ્ય બળ લગાડેલું નથી, = છતાં પણ તે સ્થાનાંતરિત થાય છે. તેથી તેના પર કાર્ય થતું નથી.
(રેલવે એન્જિન પોતાના બળતણમાં રહેલી આંતરિક ઊર્જાના ઉપયોગથી ગતિમાં આવે છે.)

2. ગૅસ ભરેલા રબરના ફુગ્ગાને છોડી દેતાં તે ઉપર તરફ ગતિ કરવા લાગે છે. અહીં ફુગ્ગા પર બળ લાગતું નથી, પણ તે સ્થાનાંતરિત થાય છે. તેથી કાર્ય થતું નથી.

નિષ્કર્ષ: પદાર્થ પર બળ લાગે તો કાર્ય થયું છે, તેમ કહેવું ખોટું છે તથા પદાર્થ સ્થાનાંતરિત થાય છે ત્યારે કાર્ય થયું છે, તેમ કહેવું પણ ખોટું છે.

પ્રવૃત્તિ 11.4 [પા.પુ. પાના નં. 148]

• કોઈ પદાર્થ ઉપર ઉઠાવો. તમારા દ્વારા પદાર્થ ઉપર લગાવેલ બળ દ્વારા કાર્ય કરાયું. પદાર્થ ઊંચો થાય છે. તમારા દ્વારા લગાવવામાં આવેલું બળ તેના સ્થાનાંતરની દિશામાં છે. જોકે પદાર્થ ઉપર ગુરુત્વીય બળ પણ કાર્યરત છે.
• આમાંથી કયું બળ ધનાત્મક કાર્ય કરી રહ્યું છે?
• કયું બળ ત્રણાત્મક કાર્ય કરી રહ્યું છે?
• કારણ બતાવો.

ચર્ચા-વિચારણા:
→ પ્રવૃત્તિકર્તા વડે લગાડેલાં બળ દ્વારા થતું કાર્ય ધન છે, કારણ કે લગાડેલું બળ (બાહ્ય બળ) અને પદાર્થના સ્થાનાંતરની દિશા એક જ છે.

→ પૃથ્વીના ગુરુત્વાકર્ષણ બળ દ્વારા થતું કાર્ય કણ છે, કારણ કે પૃથ્વીનું ગુરુત્વાકર્ષણ બળ શિરોલંબ અધોદિશામાં છે અને પદાર્થનું સ્થાનાંતર શિરોલંબ ઊર્ધ્વદિશામાં થાય છે. એટલે કે, પૃથ્વીનું ગુરુત્વાકર્ષણ બળ અને સ્થાનાંતરની દિશા પરસ્પર વિરુદ્ધ છે.

[પ્રવૃત્તિ 11.[પા.પુ. પાના નં. 149].

• ઊર્જાના ઘણા સ્ત્રોત છે. ઊર્જાના વિવિધ સ્રોતોની યાદી બનાવો.
• નાના સમૂહોમાં વિચાર-વિમર્શ કરો કે, કેવી રીતે ઊર્જાના કેટલાક
• સ્રોત સૂર્યના લીધે છે. શું ઊર્જાના કેટલાક એવા સ્રોત પણ છે, જે સૂર્યના કારણે નથી?

ચર્ચા-વિચારણા:

→ સૌર ઊર્જા, ન્યુક્લિયર ઊર્જા, પવન-ઊર્જા, સાગર-ઊર્જા, હાઇડ્રોઊર્જા (ગતિશીલ પાણી સાથે સંકળાયેલ ઊર્જા), પૃથ્વીના પેટાળમાં રહેલી ઊર્જા વગેરે.

→ સૂર્ય આપણા માટે કુદરતી ઊર્જાનો સૌથી મોટો સ્રોત છે. પવનઊર્જા, પૃથ્વીના પેટાળમાં રહેલી ઊર્જા, સાગર-ઊર્જા, સૂર્યપ્રકાશની હાજરીમાં પ્રકાશસંશ્લેષણની ક્રિયા દ્વારા લીલાં વૃક્ષોમાં ખોરાક સ્વરૂપે સંગ્રહાયેલી ઊર્જા વગેરે.
સૂર્યપ્રકાશને લીધે જમીન અને પૃથ્વી પરનું પાણી અનિયમિત રીતે ગરમ થાય છે. જેના કારણે વાતાવરણમાંની હવા ગતિમાં આવે છે, જે પવન-ઊર્જાના સ્વરૂપે હોય છે.
પૃથ્વીના પેટાળમાં ઑઇલ, કુદરતી ગૅસ, કોલસાના સ્વરૂપમાં ઊર્જા સંગ્રહાયેલી છે; જે પૃથ્વીના નિર્માણ વખતે સૌર ઊર્જાને આભારી છે. સાગરમાં આવતી ભરતી અને ઓટ સાથે પણ ઊર્જા સંકળાયેલી છે, જેમાં સૌર ઊર્જાનો પણ ફાળો છે.

→ ન્યુક્લિયર પાવર પ્લાન્ટ્સમાં વપરાતી ન્યુક્લિયર ઊર્જા, વિદ્યુતકોષોમાં સંગ્રહાયેલી રાસાયણિક ઊર્જા વગેરેમાં સૌર ઊર્જાનો ફાળો નથી.

પ્રવૃત્તિ 11.6 [પા.પુ. પાના નં 150]

• એક વજનદાર દડો લો. તેને રેતીના મોટા ઢગલા પર ફેંકો. ભીની રેતીની સપાટી પર આ પ્રવૃત્તિ સારી રીતે સમજી શકાશે. દડાને રેતી ઉપર લગભગ 25 cmની ઊંચાઈથી ફેંકો. દડો રેતીમાં એક ખાડો બનાવી દેશે.
• આ પ્રવૃત્તિ 50 cm, 1 m તથા 1.5 m ની ઊંચાઈએથી પુનરાવર્તિત કરો.
• ચોક્કસ કરો કે દરેક ખાડો સુસ્પષ્ટ દેખાય.
• દડાની ઊંચાઈ અનુસાર દરેક ખાડા પર નિશાન લગાવો.
• તેમની ઊંડાઈની સરખામણી કરો.
• તેમાંથી કયા ખાડાની ઊંડાઈ સૌથી વધુ છે?
• કયા ખાડાની ઊંડાઈ સૌથી ઓછી છે? કેમ?
• દડાએ કયા કારણસર ઊંડો ખાડો બનાવ્યો?
• વિચાર-વિમર્શ કરી, તેનું અર્થઘટન કરો.

ચર્ચા-વિચારણા:
→ દરેક ખાડાની ઊંડાઈ જુદી જુદી છે.

→ જ્યારે ભારે દડાને 1.5 m = 150 cm ઊંચાઈએથી મુક્ત કરવામાં આવે છે ત્યારે ખાડાની ઊંડાઈ સૌથી વધુ હોય છે.

→ જ્યારે ભારે દડાને 25 cm ઊંચાઈએથી મુક્ત કરવામાં આવે છે ત્યારે ખાડાની ઊંડાઈ સૌથી ઓછી છે, કારણ કે ભીની રેતીના ઢગલા પર જ્યારે ભારે દડાને ‘h’ ઊંચાઈએથી મુક્ત કરવામાં આવે છે ત્યારે તે દડો રેતીની અંદર ‘d જેટલા અંતર સુધી ઘૂસી જાય છે. અહીં રેતી વડે ભારે દડા પર અવરોધક બળ F લાગે છે.
હવે, h જેટલી ઊંચાઈએ રહેલા દડા પાસે કંઈક ઊર્જા (mgh જેટલી, જે તેની ગુરુત્વીય સ્થિતિ-ઊર્જા.) છે. તેને મુક્ત કરતાં તે ગતિમાં આવે છે ત્યારે તે સ્થિતિ) ઊર્જા, ગતિ-ઊર્જામાં રૂપાંતરિત થાય છે. આ ગતિ-ઊર્જાના ભોગે દડો રેતીની અંદર ‘d જેટલું અંતર ઘૂસી જાય છે.

જેમ દડાની ઊંચાઈ h વધુ તેમ તેની સ્થિતિ) ઊર્જા વધુ અને તેથી દડાની કાર્ય (w = Fd) કરવાની ક્ષમતા વધુ.
જે દર્શાવે છે કે d ∝ h
આમ, ઊંચાઈ h₁ = 25 cm, h₂ = 50 cm, h₃ = 100 cm, h₄ = 150 cmને અનુરૂપ ખાડાની ઊંડાઈ અનુક્રમે d₁, d₂, d₃ અને d₄ હોય, તો
d₁ : d₂ : d₃ : d₄ = 25 cm : 50 cm : 100 cm : 160 cm
= 1 : 2 : 4 : 6
∴ d₄ = 6d₁
અર્થાત્ દડાને જ્યારે 150 cm ઊંચાઈએથી મુક્ત કરવામાં આવે { છે ત્યારે મળતી ખાડાની ઊંડાઈ (d₄), 25 cm ઊંચાઈએથી મુક્ત કરેલા દડા કરતાં 6 ગણી છે. તેનું કારણ 160 cm ઊંચાઈએ દડા પાસે સૌથી વધુ (સ્થિતિ) ઊર્જા હોય છે.

નિષ્કર્ષઃ ‘h’ ઊંચાઈએથી મુક્ત પતન કરતા દડાને લીધે ભીની રેતી માટીમાં પડતા ખાડાની ઊંડાઈ ‘d’, દડાની સ્થિતિ) ઊર્જાને લીધે છે.
જેમ દડાની ઊંચાઈ ‘h વધુ તેમ તેની (સ્થિતિ) ઊર્જા વધુ અને છે પરિણામે પડતા ખાડાની ઊંડાઈ વે પણ વધુ.

પ્રવૃત્તિ 11.7 [પા.પુ. પાના નં 150]

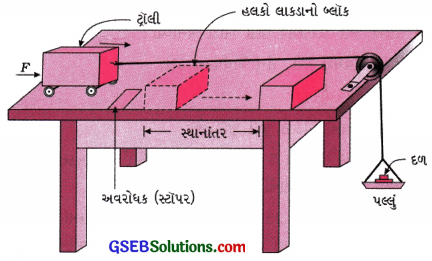
[આકૃતિ 11.6]

• આકૃતિ 11.6માં દર્શાવ્યા પ્રમાણે સાધનો ગોઠવો.
• જાણીતા દળના લાકડાના બ્લૉકને એક રૅલીની સામે ચોક્કસ અંતરે મૂકો.
• પલ્લામાં એક જાણીતું દળ મૂકો કે જેથી ટ્રૉલી ગતિ શરૂ કરે.
• સૅલી આગળ ગતિ કરીને લાકડાના બ્લૉકને અથડાશે.
• ટેબલ પર એક અવરોધક એવી રીતે રાખો કે બ્લૉકને અથડાયા બાદ ટ્રૉલી ત્યાં અટકી જાય. બ્લૉક સ્થાનાંતરિત થાય.
• બ્લૉકનું સ્થાનાંતર માપો. આનો અર્થ એ થયો કે ટ્રોલી દ્વારા બ્લૉક પર કાર્ય થયું અને બ્લૉકે ઊર્જા મેળવી.
• આ ઊર્જા ક્યાંથી આવી?
• પલ્લામાં મૂકેલા વજનમાં વધારો કરી આ પ્રવૃત્તિનું પુનરાવર્તન કરો.
• કયા કિસ્સામાં સ્થાનાંતર વધુ છે? કયા કિસ્સામાં થતું કાર્ય વધુ છે?

અવલોકન:
પૃથ્વીનું ગુરુત્વાકર્ષણ બળ પલ્લાને અને તેમાં મૂકેલા દળને નીચે તરફ ખેંચે છે. આ બળ દોરી મારફતે ટ્રૉલી પર લાગે છે. તેથી ટ્રૉલી ગતિ કરવા લાગે છે અને બ્લૉક સાથે અમુક બળથી અથડાય છે.
પરિણામે લાકડાનો બ્લૉક ગતિમાં આવે છે અને (ગતિ) ઊર્જા મેળવે છે. અર્થાત્ ટ્રૉલીની (ગતિ) ઊર્જા, બ્લૉકની (ગતિ) ઊર્જામાં અવિર્ભાવ પામે છે. બીજા શબ્દોમાં ગતિમાન ટ્રૉલી બ્લૉક પર કાર્ય કરે છે.
(પલ્લામાં મુકેલા જાણીતા દળની (ગુરુત્વીય સ્થિતિ) ઊર્જા ટ્રૉલીને ગતિ-ઊર્જારૂપે મળે છે.)

જો પલ્લામાં મુકેલા દળમાં વધારો કરવામાં આવે, તો જાણીતા દળની મોટા મૂલ્યની (ગુરુત્વીય સ્થિતિ) ઊર્જા ટ્રૉલીને ગતિ-ઊર્જારૂપે પ્રાપ્ત થાય છે. તેથી ટ્રૉલી વધુ ઝડપે ગતિ કરીને વધુ બળથી બ્લૉક સાથે અથડાય છે અને બ્લૉક પર વધુ કાર્ય કરે છે. પરિણામે દેખીતી રીતે બ્લૉકનું સ્થાનાંતર પહેલા કિસ્સા કરતાં વધુ છે.

નિષ્કર્ષ: પલ્લામાં મૂકેલા દળની (ગુરુત્વીય સ્થિતિ) ઊર્જા, ટ્રૉલીને ગતિ-ઊર્જારૂપે મળે છે. ત્યારબાદ ટ્રૉલીની અથડામણ બ્લૉક સાથે થવાથી બ્લૉક પર કાર્ય થાય છે અને બ્લૉક ગતિ-ઊર્જા મેળવે છે અને સ્થાનાંતરિત થાય છે.
આ ઊર્જાના રૂપાંતરણનો વિશિષ્ટ કિસ્સો છે.

પ્રવૃત્તિ 11.8 [પા.પુ. પાના નં. 152]

• એક રબરની રિંગ લો.
• તેના એક છેડાને પકડીને બીજો છેડો ખેંચો. રિંગ ખેંચાશે.
• રિંગના કોઈ એક છેડાને છોડી દો.
• શું થાય છે?
• સ્પષ્ટ છે કે રબરે તેના ખેંચાવાની સ્થિતિમાં કંઈક ઊર્જા મેળવી છે. ખેંચાવાથી તે કેવી રીતે ઊર્જા મેળવે છે?

અવલોકન:
અહીં રબરની રિંગને ખેંચવા માટે કરવું પડતું કાર્ય તેની અંદર સ્થિતિ-ઊર્જારૂપે સંગ્રહ પામે છે.
(પદાર્થની અંદર તેની સંરચના/પરિમાણને કારણે સંગ્રહ પામતી ઊર્જાને સ્થિતિસ્થાપકીય સ્થિતિ-ઊર્જા કહે છે.)
રિંગમાં સંગૃહીત થયેલી આ ઊર્જાને (સ્થિતિ-ઊર્જાને) લીધે, જ્યારે તેના એક છેડાને છોડી દેવામાં આવે છે ત્યારે તે પોતાની મૂળ લંબાઈ પ્રાપ્ત કરે છે.

નિષ્કર્ષ: જ્યારે પદાર્થ પર તેનો વેગ બદલ્યા વગર કાર્ય થતું હોય છે ત્યારે તે કરેલું કાર્ય તે પદાર્થની અંદર ઊર્જારૂપે સંગ્રહ પામે છે. તેને પદાર્થની સ્થિતિ-ઊર્જા કહે છે.

પ્રવૃત્તિ 11.9 [પા.પુ. પાના નં152]

• એક ક્લિંકી (Slinky – લાંબી સ્પ્રિંગ) લો.
• આકૃતિ 11.8માં દર્શાવ્યા પ્રમાણે તેનો એક છેડો તમારા મિત્રને પકડવાનું કહો. તમે બીજા છેડાને પકડો તથા મિત્રથી દૂર જાઓ.
• હવે તમે ક્લિંકીને છોડી દો. શું થાય છે?
• ખેંચવાથી કેવી રીતે ઊર્જા મેળવે છે?
• શું સંકોચન સ્થિતિમાં પણ ક્લિંકી ઊર્જા મેળવશે?

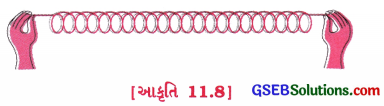
અવલોકનઃ
→ જ્યારે સ્લિકીને છોડી દેવામાં આવે છે ત્યારે તે પોતાની મૂળ લંબાઈ (સંરચના) પ્રાપ્ત કરે છે.
→ જ્યારે સ્લિકીને ખેંચવામાં આવે છે ત્યારે તેના પર કરેલું કાર્ય તેની અંદર ઊર્જારૂપે સંગ્રહ પામે છે. જેને તેની સ્થિતિ-ઊર્જા કહે છે.
→ હા, ક્લિંકીનું સંકોચન કરવા માટે પણ તેના પર કાર્ય કરવું જરૂરી છે (અર્થાત્ ઊર્જા ખર્ચવી જરૂરી છે.) અને સંકોચનની સ્થિતિમાં કરેલું આ કાર્ય તેમાં ઊર્જારૂપે સંગ્રહ પામે છે. તેને સ્થિતિ-ઊર્જા કહે છે.

નિષ્કર્ષ: ખેંચાયેલી કે સંકોચાયેલી ક્લિંકી (લાંબી સ્પ્રિંગ) સ્થિતિ? ઊર્જા ધરાવે છે. તેને સ્થિતિસ્થાપકીય સ્થિતિ-ઊર્જા કહે છે, કારણ કે 3 તેના પર થતા કાર્યને લીધે તેની સંરચના (અહીં લંબાઈ) બદલાય છે.

પ્રવૃત્તિ 11.10 [પા.પુ. પાના નં 152].

• એક રમકડાની કાર લો. એમાં ચાવી ભરો.
• કારને જમીન ઉપર મૂકો.
• શું તે ચાલે છે?
• તેણે ઊર્જા ક્યાંથી મેળવી?
• શું મેળવેલ ઊર્જા ચાવી દ્વારા ફેરવેલા આંટાઓની સંખ્યા ઉપર 3 આધારિત છે?
• તમે આની તપાસ કેવી રીતે કરશો?

અવલોકન:
→ હા, કાર ચાલે છે.
→ જ્યારે રમકડાની કારને ચાવી ભરવામાં આવે છે ત્યારે તેની અંદર રહેલી સ્પ્રિંગમાં વળ ચઢે છે. આ વળ ચઢાવવા માટે કરેલા કાર્યને લીધે સ્પ્રિંગ ઊર્જા મેળવે છે. તેને સ્થિતિસ્થાપકીય સ્થિતિ-ઊર્જા કહે છે.
→ હા.
→ જ્યારે ચાવી દ્વારા ફેરવેલા આંટાઓની સંખ્યા વધારે હશે ત્યારે મ્પિંગમાં સંગ્રહ પામેલી ઊર્જા પણ વધારે હશે અને જ્યારે સ્પ્રિંગના 4 આ વળ ઉકેલાશે ત્યારે આ ઊર્જાનું રૂપાંતરણ રમકડાની કારની – ગતિ-ઊર્જામાં થશે અને રમકડાની કાર જમીન પર વધુ અંતર કાપશે.
જો ચાવી દ્વારા ફેરવેલા આંટાઓની સંખ્યા ઓછી હોય, તો કાર જમીન પર ઓછું અંતર કાપે છે.

નિષ્કર્ષ: વળ ચઢાવેલી સ્પ્રિંગમાં સ્થિતિસ્થાપકીય સ્થિતિ-ઊર્જા સંગ્રહાયેલી હોય છે. જ્યારે આ વળ ઉકેલાવા માંડે છે ત્યારે રમકડાની કાર પર (આ સ્થિતિ-ઊર્જાને કારણે) કાર્ય થાય છે, જે કારમાં ગતિ૬ ઊર્જારૂપે આવિર્ભાવ પામે છે અને કાર જમીન પર સ્થાનાંતરિત થાય છે.

પ્રવૃત્તિ 11.11 [પા.પુ. પાના નં. 152]

• કોઈ પદાર્થને એક ચોક્કસ ઊંચાઈ સુધી ઊઠાવો.
• પદાર્થ હવે કાર્ય કરી શકે છે. છોડી દેવાથી તે નીચે પડે છે. આનો અર્થ એ થાય છે કે એણે થોડીક ઊર્જા ધારણ કરી લીધી છે.
• વધુ ઊંચે લઈ જતા તે વધારે કાર્ય કરી શકે છે અને આ પ્રકારે એમાં વધારે ઊર્જાનો સંગ્રહ થઈ જાય છે.
• આને ઊર્જા ક્યાંથી મળે છે? તે વિચારો અને વિચાર-વિમર્શ કરો.

અવલોકન:
→ જ્યારે પદાર્થને પૃથ્વીની સપાટી (જમીન) પરથી અમુક ચોક્કસ ઊંચાઈ સુધી ઊઠાવવામાં આવે છે ત્યારે તેના પર લાગતા પૃથ્વીના ગુરુત્વાકર્ષણ બળ વિરુદ્ધ તેના પર કાર્ય થાય છે.
→ આ કરેલું કાર્ય, આ સ્થાને તેમાં ઊર્જારૂપે સંગ્રહ પામે છે. તેને પદાર્થની ગુરુત્વીય સ્થિતિ-ઊર્જા કહે છે.
→ જો પદાર્થને વધારે ઊંચાઈએ લઈ જવો હોય, તો દેખીતી રીતે તેના પર વધુ કાર્ય કરવું પડે. પરિણામે પદાર્થની ગુરુત્વીય સ્થિતિ-ઊર્જા વધે છે અને પદાર્થ વધારે કાર્ય કરી શકે છે.

નિષ્કર્ષ: પદાર્થને જમીન પરથી અમુક ચોક્કસ ઊંચાઈ સુધી ઊઠાવવામાં આવે છે ત્યારે તેના પર લાગતા પૃથ્વીના ગુરુત્વાકર્ષણ બળ વિરુદ્ધ તેના પર કાર્ય થાય છે.
પરિણામે અહીં પદાર્થ પોતાના સ્થાનને લીધે પૃથ્વીની સપાટી(જમીન)ની સાપેક્ષે ઊર્જા ધરાવે છે. તેને પદાર્થની ગુરુત્વીય સ્થિતિ-ઊર્જા કહે છે.
પૃથ્વીની સપાટીથી પદાર્થની ઊંચાઈ જેમ વધુ તેમ તેની ગુરુત્વીય સ્થિતિ-ઊર્જા વધુ.

પ્રવૃત્તિ 11.12 [પા.પુ. પાના નં. 152]

• વાંસની એક પટ્ટી લો અને તેમાંથી આકૃતિ 11.9માં દર્શાવ્યા પ્રમાણે એક ધનુષ્ય તૈયાર કરો.
• એક હલકી દંડીનું તીર બનાવો.
• તીરનો એક છેડો ધનુષ્ય પર ખેંચીને બાંધેલી દોરી પર રાખો.
• હવે દોરીને ખેંચી તીરને છોડો.
• તીર ધનુષ્યથી દૂર જાય છે તે નોંધો તથા ધનુષ્યના આકારમાં થતો ફેરફાર નોંધો.

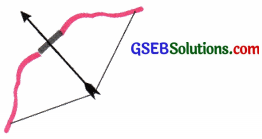
[આકૃતિ 11.9: ધનુષ્યની તાણેલી દોરી પર રાખેલ તીર]

અવલોકન:
→ જ્યારે ધનુષ્યની દોરીને તીર સહિત ખેંચવામાં આવે છે ત્યારે તેના પર થતા કાર્યને લીધે ધનુષ્યનો આકાર સંરચના બદલાય છે અને કરેલું કાર્ય તેમાં સ્થિતિસ્થાપકીય સ્થિતિ-ઊર્જારૂપે સંગ્રહ પામે છે.

→ જ્યારે તીરને અને દોરીને છોડવામાં આવે છે ત્યારે ધનુષ્યમાં સંગ્રહાયેલી સ્થિતિ-ઊર્જાને કારણે તીર પર કાર્ય થાય છે, જે તીરની ગતિ-ઊર્જામાં અવિર્ભાવ પામે છે. પરિણામે તીર ગતિ કરીને દૂર પડે છે.

નિષ્કર્ષ: તીર સહિત ધનુષ્યની દોરીની ખેંચાયેલી સ્થિતિમાં તેમાં સ્થિતિસ્થાપકીય સ્થિતિ-ઊર્જા સંગ્રહાયેલી હોય છે. જ્યારે તીર અને દોરીને છોડવામાં આવે છે ત્યારે તે સ્થિતિ-ઊર્જાનું તીરની ગતિ-ઊર્જામાં રૂપાંતરણ થાય છે. પરિણામે તીર દૂર તરફ ગતિ કરીને પડે છે.

પ્રવૃત્તિ 11.13 [પા.પુ. પાના નં 154]

• નાનાં નાનાં જૂથમાં બેસો.
• કુદરતમાં ઊર્જાનાં રૂપાંતરણના જુદા જુદા પ્રકારો વિશે ચર્ચા કરો.
• તમારા સમૂહમાં નીચેના પ્રશ્નો વિશે વિચાર-વિમર્શ કરો:
  1. લીલાં પણ ખોરાક કેવી રીતે બનાવે છે?
  2. તેમને ઊર્જા ક્યાંથી પ્રાપ્ત થાય છે?
  3. વાયુ એક સ્થળેથી બીજા સ્થળે કેમ વહે છે?
  4. કોલસો તથા પેટ્રોલિયમ જેવાં ઈંધણ કેવી રીતે બન્યા?
  5. કયા પ્રકારનાં ઊર્જાનાં રૂપાંતરણો જલચક્રને ટકાવી રાખે છે?

ચર્ચા-વિચારણા:
1. લીલાં પર્ણો સૂર્યપ્રકાશની હાજરીમાં પ્રકાશસંશ્લેષણની ક્રિયા દ્વારા ખોરાક બનાવે છે.

2. લીલાં પર્ણો સૌર ઊર્જામાંથી ઊર્જા પ્રાપ્ત કરે છે.

3. સૌર ઊર્જાને કારણે પૃથ્વી પરની જમીન, દરિયાનું પાણી અને વાતાવરણ અનિયમિત રીતે ગરમ થાય છે. પરિણામે પૃથ્વી પર જુદા જુદા સ્થળે દબાણનો તફાવત ઉદ્ભવે છે. આ દબાણના તફાવતને લીધે વાયુ / હવા એક સ્થળેથી બીજા સ્થળે વહે છે.

4. લાખો વર્ષો પહેલાં વનસ્પતિ અને પ્રાણીઓના અવશેષ – પૃથ્વીની અંદર દટાઈ ગયા હતા. જુદી જુદી ક્રિયાઓ, ઊંચું દબાણ અને તાપમાનના કારણે તેઓ કોલસો પેટ્રોલિયમ(પેટ્રોલ-ઑઇલ)માં ફેરવાયા.
આમ, કોલસો તથા પેટ્રોલિયમ જેવાં ઈંધણ બન્યાં.

5. સમુદ્ર, નદીઓ, તળાવો અને વૃક્ષોમાં રહેલ પાણીનું બાષ્પીભવન સૌર ઊર્જાને કારણે થાય છે અને પાણીની વરાળ અવકાશમાં જઈને વાદળોનું નિર્માણ કરે છે. બીજા શબ્દોમાં પાણીની ગુરુત્વીય સ્થિતિ-ઊર્જા બદલાય છે.
ત્યારબાદ વરાળનું કારણ ઘનીકરણ થવાથી વરસાદ વરસે છે અને નદીઓમાં પાણી વહેવા લાગે છે. ડેમમાં સંગ્રહાયેલ પાણી સ્થિતિઊર્જા ધરાવે છે અને નદીઓમાં વહેતું પાણી ગતિ-ઊર્જા ધરાવે છે, જે જલવિદ્યુત પ્લાન્ટમાં વિદ્યુત-ઊર્જામાં રૂપાંતરિત થાય છે.
આમ, ઊર્જાનાં રૂપાંતરણો કુદરતમાં અગત્યનો ભાગ ભજવે છે અને જલચક્રને ટકાવી રાખે છે, જેના લીધે સજીવસૃષ્ટિ જીવંત રહી શકે છે.

પ્રવૃત્તિ 11.14 [પા.પુ. પાના નં. 154]

• અનેક માનવ-પ્રવૃત્તિઓ તથા આપણા દ્વારા ઉપયોગમાં લેવાતાં ઉપકરણો(Gadgets)માં ઊર્જાનું રૂપાંતરણ સામેલ થયેલું હોય છે.
• આવા પ્રકારની પ્રવૃત્તિઓ તથા ઉપકરણોની સૂચિ બનાવો.
• દરેક પ્રવૃત્તિ તથા ઉપકરણમાં કયા પ્રકારની ઊર્જા રૂપાંતરિત થાય છે તે ઓળખી બતાવો.

ચર્ચા-વિચારણા:
માનવ-પ્રવૃત્તિઓ દોડવું, સાઇકલ ચલાવવી, તરવું વગેરે.
ઉપયોગી ઉપકરણોઃ ઇલેક્ટ્રિક મોટર, ઇલેક્ટ્રિક હીટર, ઇલેક્ટ્રિક . ઇસ્ત્રી, ઇલેક્ટ્રિક ગીઝર, ઇલેક્ટ્રિક ઓવન, ઇલેક્ટ્રિક સેલ, સોલર સેલ, ફોટોઇલેક્ટ્રિક સેલ, ડાયનેમો, સ્ટીમ એન્જિન / ઉષ્મા એન્જિન, માઇક્રોફોન, લાઉડસ્પીકર, ઇલેક્ટ્રિક બલ્બ, ગૅસ સ્ટવ, ગેસ ગીઝર, સોલર વૉટરહીટર વગેરે.

→ મોટા ભાગની માનવ-પ્રવૃત્તિઓમાં સ્નાયુઓની ઊર્જા, ગતિ-ઊર્જામાં રૂપાંતરિત થાય છે, પછી ગતિ-ઊર્જાનું રૂપાંતરણ ઉષ્મા-ઊર્જામાં થાય છે.

• ઇલેક્ટ્રિક મોટર: વિદ્યુત-ઊર્જાનું યાંત્રિક ઊર્જામાં રૂપાંતરણ
• ઇલેક્ટ્રિક હીટર, ઇલેક્ટ્રિક ઇસ્ત્રી, ઇલેક્ટ્રિક ગીઝર, ઇલેક્ટ્રિક
  ઓવન: વિદ્યુત-ઊર્જાનું ઉષ્મા-ઊર્જામાં રૂપાંતરણ
• ઇલેક્ટ્રિક સેલઃ રાસાયણિક ઊર્જાનું વિદ્યુત-ઊર્જામાં રૂપાંતરણ
• સોલર સેલ: સૌર ઊર્જાનું વિદ્યુત-ઊર્જામાં રૂપાંતરણ
• ફોટોઇલેક્ટ્રિક સેલ: પ્રકાશ-ઊર્જાનું વિદ્યુત-ઊર્જામાં રૂપાંતરણ
• ડાયનેમો: યાંત્રિક ઊર્જાનું વિદ્યુત-ઊર્જામાં રૂપાંતરણ
• સ્ટીમ એન્જિન/ઉષ્મા એન્જિન: ઉષ્મા-ઊર્જાનું યાંત્રિક ઊર્જામાં રૂપાંતરણ
• માઈક્રોફોન: ધ્વનિ-ઊર્જાનું વિદ્યુત-ઊર્જામાં રૂપાંતરણ
• લાઉડસ્પીકર: વિદ્યુત-ઊર્જાનું ધ્વનિ-ઊર્જામાં રૂપાંતરણ
• ઇલેક્ટ્રિક બલ્બ વિદ્યુત-ઊર્જાનું પ્રકાશ-ઊર્જામાં રૂપાંતરણ
• ગૅસ સ્ટવ, ગેસ ગીઝર : રાસાયણિક ઊર્જાનું ઉષ્મા-ઊર્જામાં રૂપાંતરણ
• સોલર વૉટરહીટર: પ્રકાશ-ઊર્જાનું ઉષ્મા-ઊર્જામાં રૂપાંતરણ

પ્રવૃત્તિ 11.15 [પા.પુ. પાના નં. 155]

20 kg દળનો કોઈ પદાર્થ 4 mની ઊંચાઈથી મુક્ત પતન પામે છે. નીચેના કોષ્ટક અનુસાર દરેક સ્થિતિમાં સ્થિતિ-ઊર્જા તથા ગતિઊર્જાની ગણતરી કરો અને કોષ્ટકમાં ખાલી સ્થાનોની પૂર્તિ કરો:

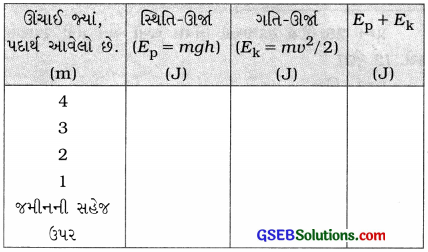
ગણતરીની સરળતા ખાતર કુનું મૂલ્ય 10 m s^-2 લો.
ઉકેલ:
(1) જ્યારે h = 4 m
ત્યારે E_p = mgh = 20 × 10 × 4 J = 800 J
E_k = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) × 20 × (0)² = 0 J

(2) જ્યારે n = 3 m
ત્યારે E_p = mgh = 20 × 10 × 3 = 600 J
મુક્ત પતન દરમિયાન પદાર્થે કાપેલું અંતર (s) = (4 – 3)m
= 1 m
હવે, અહીં V² = u² + 2gs = 0 + 2gs = 2gs
∴ E = \(\frac{1}{2}\)mv²
= \(\frac{1}{2}\)m (2gs) = mgs
= 20 × 10 × 1
= 200 J

(3) જ્યારે h = 2 m
ત્યારે E_p = mgh = 20 × 10 × 2 = 400 J
મુક્ત પતન દરમિયાન પદાથે કાપેલું અંતર (s) = (4 – 2) m
= 2 m
∴ E_k = mgs = 20 × 10 × 2 = 400 J

(4) જ્યારે h = 1 m
ત્યારે E_p = mgh = 20 × 10 × 1 = 200 J
મુક્ત પતન દરમિયાન પદાર્થે કાપેલું અંતર (s) = (4 – 1) m
= 3 m
∴ E_k = mgs = 20 × 10 × 3 = 600 J

(5) જમીનથી સહેજ ઉપર,
h = 0, = (4 – 0) m = 4 m
E_p = mgh = 20 × 10 × 0 = 0 J
E_k = mgs = 20 × 10 × 4 = 800 J
હવે, સંપૂર્ણ ભરેલું કોષ્ટક નીચે મુજબ થશે:

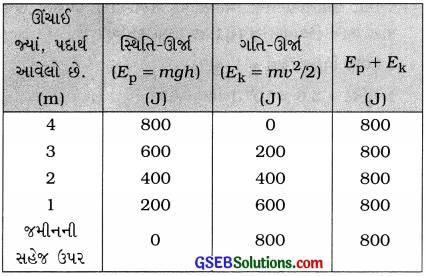
અવલોકનઃ ઉપરના કોષ્ટકમાં પદાર્થની આપેલી જુદી જુદી ઊંચાઈ h ને અનુરૂપ પદાર્થની સ્થિતિ-ઊર્જા E_p અને ગતિ-ઊર્જા E_k નાં મૂલ્યો પરથી સ્પષ્ટ છે કે, જેમ જેમ ઊંચાઈ ક્રમશઃ ઘટે છે તેમ તેમ સ્થિતિઊર્જા જેટલા પ્રમાણમાં ઘટે છે, તેટલા જ પ્રમાણમાં ગતિ-ઊર્જા વધે છે અને સ્થિતિ-ઊર્જા તથા ગતિ-ઊર્જાનો સરવાળો અચળ જળવાઈ રહે છે.

નિષ્કર્ષ: અમુક ઊંચાઈથી (અહીં 4 m) મુક્ત પતન કરતા પદાર્થની યાંત્રિક ઊર્જા દરેક ઊંચાઈ માટે અચળ જળવાઈ રહે છે. તેનો અર્થ યાંત્રિક ઊર્જા E = સ્થિતિ-ઊર્જા E, + ગતિ-ઊર્જા EWS સંરક્ષણ થાય છે.

આ વિશે વિચારો:
જો કુદરતમાં ઊર્જાનું રૂપાંતરણ શક્ય ન હોત તો શું થાત? એક વિચાર અનુસાર ઊર્જાના રૂપાંતરણ વિના જીવન શક્ય જ ન બનત. શું તમે આ હકીકત સાથે સહમત છો?
→ હા.
→ પૃથ્વી ઉપર સજીવસૃષ્ટિનું જીવન શક્ય બને એટલા માટે ખોરાક અગત્યનો છે.
→ લીલી વનસ્પતિ સૌર ઊર્જાના ઉપયોગથી ખોરાક બનાવે છે. આ પ્રકાશસંશ્લેષણની પ્રક્રિયામાં સૂર્યની પ્રકાશ-ઊર્જાનું ખોરાકની રાસાયણિક ઊર્જામાં રૂપાંતરણ થાય છે.
→ ફોટો વૉલ્ટેક સેલ (કોષ) વડે સૌર ઊર્જાનું વિદ્યુત-ઊર્જામાં રૂપાંતરણ થાય છે.
→ જલ-ઊર્જા અને પવન-ઊર્જા પણ સૌર ઊર્જાનાં બીજાં સ્વરૂપો છે.
આમ, સ્પષ્ટ છે કે ઊર્જાના રૂપાંતરણ વિના સજીવસૃષ્ટિનું જીવન શક્ય બને નહિ.

પ્રવૃત્તિ 11.16 [પા.પુ. પાના નં. 155]

• બે બાળકો ધારો કે A અને Bનો વિચાર કરો. ધારો કે, તેમનાં દળ સમાન છે. બંને દોરડા પર અલગ અલગ ચડવાનો પ્રારંભ કરે છે. બંને 8 mની ઊંચાઈ સુધી પહોંચે છે. માની લો કે આ કાર્ય કરવામાં A 15 sનો સમય લે છે જ્યારે B20 sનો સમય લે છે.
• દરેક બાળક દ્વારા થયેલ કાર્ય કેટલું છે?
• કયા બાળકે આપેલ સમય ધારો કે 1 sમાં વધારે કાર્ય કર્યું છે?

ચર્ચા-વિચારણા:
→ દરેક બાળક દ્વારા થયેલ કાર્ય સમાન છે અને તે mgh જેટલું છે, કારણ કે બંને બાળકોનાં દળ m સમાન છે અને તેઓ સમાન
અંતર 8 m ઊર્ધ્વદિશામાં કાપે છે.
→ હવે, અહીં
1 sમાં બાળક A દ્વારા થયેલ કાર્ય = \(\left[\frac{m g h}{15}\right]\) એકમ અને
1 sમાં બાળક B દ્વારા થયેલ કાર્ય = \(\left[\frac{m g h}{20}\right]\) એકમ
હવે, \(\left[\frac{m g h}{15}\right]\) > \(\left[\frac{m g h}{20}\right]\)

∴ બાળક A 1 sમાં બાળક B કરતાં વધુ કાર્ય કરે છે, એટલે કે
બાળક A નો કાર્ય કરવાનો સમયદર બાળક B કરતાં વધુ છે.

નિષ્કર્ષ: જુદી જુદી વ્યક્તિઓ/એજન્સીઓ દ્વારા થતા કાર્યનાં – મૂલ્યો સમાન હોય પણ જો તે કાર્ય કરવા માટે તેમણે લીધેલા સમય અસમાન હોય, તો જે વ્યક્તિ/એજન્સી ઓછો સમય લે છે તે 1 sમાં વધુ કાર્ય કરે છે. અર્થાત્ તેનો કાર્ય કરવાનો સમયદર વધુ હોય છે.

પ્રવૃત્તિ 11.17 [પા.પુ. પાના નં. 157]

• તમારા ઘરમાં વિદ્યુત પરિપથમાં લગાડેલ વિદ્યુત મિટરને ધ્યાનપૂર્વક જુઓ. તેની વિશેષતાઓ બારીકાઈથી જુઓ.
• દરરોજ સવારે 6:30 વાગે તથા સાંજે 6:30 વાગે વિદ્યુત મિટરનું વાંચન કરો.
• દિવસમાં કેટલા યુનિટ’ વપરાય છે?
• રાતના સમયે કેટલા યુનિટ’ વપરાય છે?
• આ પ્રવૃત્તિ લગભગ 1 અઠવાડિયા સુધી કરો.
• તમારાં અવલોકનોને કોષ્ટકમાં નોંધો.
• આ અવલોકનો પરથી નિષ્કર્ષ તારવો.
• તમારાં અવલોકનોની તુલના વિદ્યુતના માસિક બિલ સાથે તેમાં આપેલ માહિતી સાથે કરો.

ચર્ચા-વિચારણા:
→ ધારો કે, સોમવારે સવારે 6:30 વાગે વિદ્યુત મિટરનું અવલોકન A₁ અને સાંજે 6:30 વાગે B₁ મળે છે, તો B₁ – A₁, કરવાથી સોમવારે દિવસ દરમિયાન વપરાયેલા યુનિટની સંખ્યા જાણી શકાય છે.

બીજા દિવસે મંગળવારે સવારે 6:30 વાગે લીધેલા અવલોકન A₂ માંથી B₁ બાદ કરવાથી સોમવાર રાતના સમયગાળા દરમિયાન વપરાયેલા યુનિટ જાણી શકાય છે.

→ આ રીતે મહિનાની શરૂઆતમાં અને અંતે વિદ્યુત મિટરના અવલોકન લઈને સમગ્ર મહિના દરમિયાન વપરાયેલા કુલ યુનિટની સંખ્યા ગણી શકાય છે.

→ આ કુલ યુનિટની સંખ્યાને 1 યુનિટની મૂળ કિંમત એટલે કે ભાવ વડે ગુણવાથી આખા મહિનાનું વીજળી વપરાશનું સાચું બિલ કેટલું આવશે તે ગણી શકાય છે. પણ ઘરે આવતા વીજળીના બિલમાં જુદા જુદા વેરાઓ/ચાર્જિસ પણ ઉમેરાયેલા હોય છે.