GSEB Solutions Class 9 Science Chapter 8 ગતિ

Gujarat Board GSEB Solutions Class 9 Science Chapter 8 ગતિ Textbook Questions and Answers, Intext Questions, Textbook Activities Pdf.

ગતિ Class 8 GSEB Solutions Science Chapter 9

GSEB Class 9 Science ગતિ Textbook Questions and Answers

સ્વાધ્યાયના પ્રશ્નોત્તર

પ્રશ્ન 1.
એક ઍપ્લેટ 200 m વ્યાસ ધરાવતા વર્તુળાકાર પથ પર એક ચક્કર 40 sમાં પૂરું કરે છે. 2 min 20 s બાદ તેણે કેટલું અંતર કાપ્યું હશે તથા તેનું સ્થાનાંતર કેટલું હશે?
ઉકેલ:
વર્તુળાકાર માર્ગનો વ્યાસ = 200 m
∴ ત્રિજ્યા r = 100 m
વર્તુળ પથ પર એક ચક્કર પૂર્ણ કરવા લાગતો સમય = 40 s
∴ 2 minute અને 20 s = 140 sમાં ઍપ્લેટ \(\frac{140}{40}\) = 3.5 ચક્કર પૂર્ણ કરશે.

→ 1 ચક્કર પૂર્ણ થતા કાપેલું અંતર = વર્તુળ પથનો પરિઘ
= 2πr

∴ 3.5 ચક્કર પૂર્ણ થતા કાપેલું અંતર = 2πr × 3.5
= 2 × \(\frac{22}{7}\) × 100 × 3.5
= 2200 m

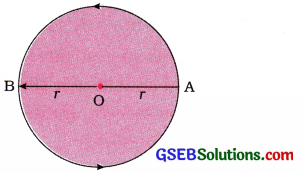
→ 3.5 ચક્કર પૂર્ણ થતા ઍપ્લેટ વર્તુળ પથ પર વ્યાસના બીજા છેડે હશે.
∴ ઍપ્લેટનું સ્થાનાંતર = વર્તુળનો વ્યાસ = 2r = 200 m
આમ, અંતર = 2200 m અને સ્થાનાંતર = 200 m

પ્રશ્ન 2.
300 mના સીધા રસ્તા પર જોસેફ જૉગિંગ કરતો કરતો 2 min 30 sમાં એક છેડા Aથી બીજા છેડા B સુધી પહોંચે છે. ત્યાંથી ? પાછો ફરી 1 મિનિટમાં 100 m પાછળ રહેલા બિંદુ C પર પહોંચે છે. જોસેફની સરેરાશ ઝડપ અને સરેરાશ વેગ
(a) A છેડાથી 3 છેડા સુધી તથા
(b) A છેડાથી C છેડા સુધી કેટલો હશે?
ઉકેલઃ

(a) Aથી B દરમિયાનની ગતિ માટે,
કાપેલું અંતર = 300 m = સ્થાનાંતર
જરૂરી સમય = 2 min 30 s
= (2 × 60) + 30
= 150 s
સરેરાશ ઝડપ =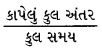
= \(\frac{300 \mathrm{~m}}{150 \mathrm{~s}}\) = 2 m s^-1
→ સરેરાશ વેગ પણ 2 m s^-1 થશે.

(b) Aથી તે દરમિયાનની ગતિ માટે,
કાપેલું અંતર = (300 + 100) m = 400 m
સ્થાનાંતર = AB – BC = (300 – 100) = 200 m
જરૂરી સમય = 2 min 30 s + 1 min
= (150 + 60) s = 210 s

આમ, (a) સરેરાશ ઝડપ = 2 m s^-1 = સરેરાશ વેગ
(b) સરેરાશ ઝડપ = 1.90 m s^-1;
સરેરાશ વેગ = 0.95 m s^-1

પ્રશ્ન 3.
અબ્દુલ ગાડી દ્વારા શાળાએ જતી વખતે સરેરાશ ઝડપ 20 km h^-1 માપે છે. તે જ રસ્તા પર પાછા ફરતી વખતે ટ્રાફિક ઓછો હોવાને કારણે તે 30 km h^-1 સરેરાશ ઝડપ માપે છે. અબ્દુલની સમગ્ર મુસાફરી દરમિયાન સરેરાશ ઝડપ કેટલી હશે?
ઉકેલ:
ધારો કે, ઘરથી શાળાનું અંતર x km છે.

આમ, અબ્દુલની સમગ્ર ગતિ (મુસાફરી) માટેની સરેરાશ ઝડપ = 24 km h^-1 હશે.

પ્રશ્ન 4.
તળાવમાં સ્થિર અવસ્થામાં રહેલી એક મોટરબોટ સુરેખ પથ પર 3.0 m sના અચળ પ્રવેગથી 8.0 s સુધી ગતિ કરે છે. આ સમયગાળામાં મોટરબોટ કેટલી દૂર ગઈ હશે? [1 ગુણ)
ઉકેલ:
અહીં, u = 0; t = 8.0 s; a = 3.0 m s^-2
મોટરથી ચાલતી હોડી (મોટરબોટ) વડે કપાયેલું અંતર,
s = ut + \(\frac{1}{2}\)at²
= 0 × 8 + \(\frac{1}{2}\) × 3 × (8)²
= 0 + 96 m
= 96 m
આમ, મોટરબોટે કાપેલું અંતર = 96 m

પ્રશ્ન 5.
52 km h^-1ની ઝડપથી ગતિ કરતી કારનો ડ્રાઇવર બ્રેક મારતાં, કારમાં ગતિની વિરુદ્ધ દિશામાં અચળ પ્રવેગ ઉત્પન થાય છે. 3 કાર 5sમાં અટકી જાય છે. બીજો ડ્રાઈવર 34 km h^-1ની ઝડપથી ગતિ કરતી બીજી કાર પર ધીમેથી બ્રેક લગાડતાં તે 10 sમાં અટકે છે. એક જ આલેખ(ગ્રાફ)પેપર પર ઝડપ વિરુદ્ધ સમયનો આલેખ બંને કાર માટે દોરો. બ્રેક લગાડ્યા બાદ બંનેમાંથી કઈ કાર વધારે દૂર સુધી જશે?
ઉકેલ:

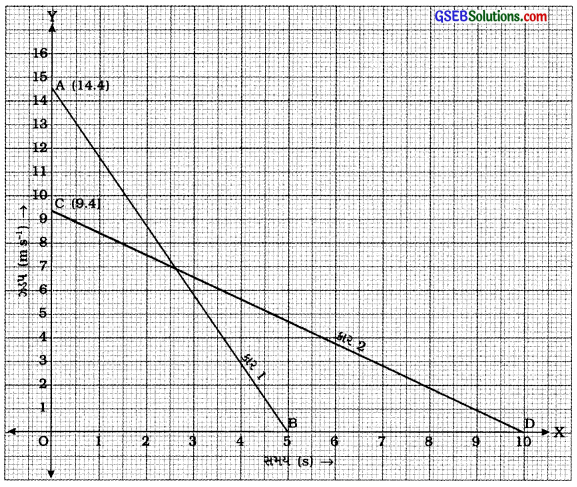
[આકૃતિ 8.27: કાર 1 અને કાર 2 માટે ઝડપ – સમયના આલેખ]

કાર 1
કાર 1 માટે પ્રારંભિક ઝડપ u = 52 km h^-1
= \(\frac{52 \times 1000 \mathrm{~m}}{3600 \mathrm{~s}}\)
= 14.44 m s^-1
→ સ્થિર થવા સુધીમાં કારે કાપેલું અંતર,
s₁ = કાટકોણ ત્રિકોણ ACBનું ક્ષેત્રફળ
= \(\frac{1}{2}\) × 14.44 × 5
= 36.1 m …… (1)

કાર 2
કાર 2 માટે પ્રારંભિક ઝડપ u = 34 km h^-1
= \(\frac{34 \times 1000 \mathrm{~m}}{3600 \mathrm{~s}}\)
= 9.44 m s^-1
→ સ્થિર થવા સુધીમાં કારે કાપેલું અંતર, sp = કાટકોણ ત્રિકોણ COD નું ક્ષેત્રફળ
= \(\frac{1}{2}\) × 9.44 × 10
= 47.2 m …….. (2)

→ (1) અને (2) પરથી સ્પષ્ટ છે કે બ્રેક લગાડ્યા પછી કાર 2, કાર 1 કરતાં વધારે અંતર કાપે છે.
વિશેષ:
કાર 1 માટે પ્રારંભિક ઝડપ u = 14.44 m s^-1
અંતિમ ઝડપ v = 0, સમય t = 5 s
પ્રવેગ a = \(\frac{v-u}{t}\) = \(\frac{0-14.44}{5}\) = – 2.888 m s^-2
સ્થિર થવા સુધીમાં કાપેલું અંતર,
s₁ = ut + \(\frac{1}{2}\)at²
= 14.44 × 5 + \(\frac{1}{2}\)(-2.888) (5)²
= 72.2 – 36.1
= 36.1 m

કાર 2 માટે પ્રારંભિક ઝડપ u = 9.44 m s^-1
અંતિમ ઝડપ v = 0, સમય t = 10 s
પ્રવેગ a = \(\frac{v-u}{t}\) = \(\frac{0-9.44}{10}\)= – 0.944 m s^-2
સ્થિર થવા સુધીમાં કાપેલું અંતર,
s₂ = ut + \(\frac{1}{2}\)at²
= 9.44 × 10 + \(\frac{1}{2}\)(- 0.944) (1o)²
= 94.4 – 47.2
= 47.2 m

પ્રશ્ન 6.
આકૃતિ 8.28માં ત્રણ વાહનો A, B અને C માટે ? અંતર – સમયનો આલેખ દર્શાવેલ છે. આલેખનો અભ્યાસ કરી નીચેના પ્રશ્નોનો ઉત્તર આપો:

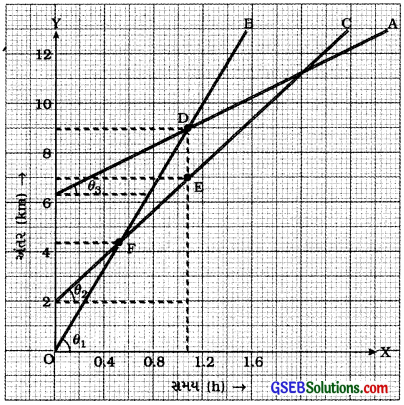
(a) ત્રણેયમાંથી સૌથી વધારે ઝડપથી કોણ ગતિ કરે છે?
(b) શું ત્રણેય કોઈ સમયે રોડ પરના એક જ બિંદુએ હશે?
(c) જ્યારે B, A પાસેથી પસાર થાય ત્યારે તું કેટલે દૂર હશે?
(d) જ્યારે B, C પાસેથી પસાર થાય તે સમય દરમિયાન તેણે કેટલું અંતર કાપ્યું હશે?
ઉકેલઃ
(a) ઝડપ = અંતર વિરુદ્ધ સમયના આલેખનો ઢાળ = tan 0
અત્રે, આપેલ આકૃતિ પરથી θ₁ > θ₂ > θ₃
∴ tan θ₁, > tan θ₂ > tan θ₃ થાય.
∴ (Bની ઝડ૫) > (Cની ઝડપ) > (Aની ઝડપ)
∴ B વાહન સૌથી વધુ ઝડપે ગતિ કરે છે.

(b) રોડ પર ત્રણેય વાહનો એકસાથે ત્યારે જ જોવા મળે કે જ્યારે ત્રણેય વાહનોના આનુષાંગિક અંતરો અને સમયનાં મૂલ્યો એકસમાન હોય, એટલે કે અંતર – સમયના આલેખો ત્રણેય વાહનો માટે એક સામાન્ય બિંદુ આગળ છેદે.
પણ આપેલ આકૃતિમાં આવું એક પણ સામાન્ય છેદનબિંદુ નથી. તેથી ત્રણેય વાહનો એકબીજાને એક સામાન્ય બિંદુ પાસે મળશે નહીં.

(c) આપેલ આકૃતિ પરથી સ્પષ્ટ છે કે વાહન B, વાહન મને D બિંદુ આગળ પસાર કરે છે. આ વખતે વાહન C, E બિંદુ પાસે હશે, જેનો 1-યામ 7 km છે.
∴ જ્યારે B, A પાસેથી પસાર થશે ત્યારે ? ઊગમબિંદુથી 7 km અંતરે હશે. (C એ કાપેલું અંતર (7 – 2) km = 5 km).

(d) આપેલ આકૃતિ પરથી સ્પષ્ટ છે કે B, Cને F બિંદુ આગળ પસાર કરે છે. ” બિંદુનું ઊગમબિંદુથી અંતર 4.5 km છે.
∴ જ્યારે B, C પાસેથી પસાર થશે ત્યારે B ઊગમબિંદુથી 4.5 km અંતરે હશે. (B એ કાપેલું અંતર 4.5 km)

પ્રશ્ન 7.
20 mની ઊંચાઈ પરથી એક દડાને નીચે પડવા દેવામાં આવે છે. જો તેનો વેગ 10 m s^-2ના નિયમિત પ્રવેગથી વધતો હોય, તો તે કેટલા વેગથી જમીન સાથે અથડાશે? કેટલા સમય બાદ તે જમીન સાથે અથડાશે?
ઉકેલ:
અત્રે, u = 0; a = 10 m s^-2 s = 20 m
2as = v² – u²
∴ 2 (10) (20) = v² – 0
∴ v² = 400 m² s²
∴ v = 20 m s^-1
હવે, v = u + at
∴ 20 = 0 + 10 (1)
∴ t = \(\frac{20}{10}\) = 2 s
આમ, દડો જમીનને 20 m s^-1 જેટલા વેગથી અથડાશે અને ગતિની શરૂઆત કર્યા બાદ 2 s પછી જમીનને અથડાશે.

પ્રશ્ન 8.
આકૃતિ 8.29માં ઝડપ – સમયનો આલેખ એક ગતિ કરતી કાર માટે દર્શાવેલ છે.

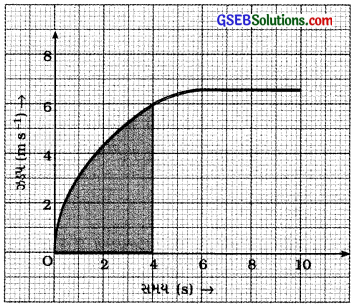
આકૃતિ 8.29
(a) પ્રથમ 4sમાં કાર કેટલું અંતર કાપશે? આ સમયગાળા દરમિયાન કાર દ્વારા કાપેલ અંતરને આલેખમાં છાયાંકિત કરો.
(b) આલેખનો કયો ભાગ કારની અચળ ગતિ દર્શાવે છે?
ઉકેલ:
(a) આપેલ આલેખ પરથી …..
સમય-અક્ષ પર 10 અતિ નાના વિભાગ = 2 s
ઝડપ-અક્ષ પર 10 અતિ નાના વિભાગ = 2 m s^-1
∴ 10 × 10 = 100 અતિ નાના ચોરસ
= 2 s × 2 m s^-1 = 4 m

→ પ્રથમ 4 s દરમિયાન ઝડપ – સમયના આલેખ અને સમય-અક્ષ વડે ઘેરાતા વિસ્તારનું (બંધગાળાનું) ક્ષેત્રફળ = 400 નાના ચોરસ (લગભગ).

અત્રે છાયાંકિત ભાગમાંના અતિ નાના ચોરસોની સંખ્યા ગણતી વખતે જે ચોરસ અડધા કે તેના કરતાં વધુ છાયાંકિત છે તેમને પૂર્ણ ચોરસ તરીકે ગણ્યાં છે, જ્યારે જે અતિ નાના ચોરસ અડધાથી ઓછા છાયાંકિત છે તેમને ગણતરીમાં લીધા નથી.
હવે, અતિ નાના ચોરસોની સંખ્યા → અનુરૂપ અંતર
100 :: 4 m
400 :: (?)
∴ પ્રથમ ચાર સેકન્ડ દરમિયાન કારે કાપેલું અંતર
= \(\frac{400 \times 4 \mathrm{~m}}{100}\) = 16.0 m (લગભગ)

(b) અચળ ગતિમાં પદાર્થની ઝડપ સમય સાથે અચળ રહે છે.
∴ t = 6 s થી લઈને t = 10 s સુધીના આલેખના
ભાગમાં કાર અચળ ગતિ કરશે.

પ્રશ્ન 9.
નીચેના પૈકી કઈ પરિસ્થિતિ શક્ય છે તથા દરેકનાં ઉદાહરણ આપો:
(a) કોઈ પદાર્થ કે જેનો પ્રવેગ અચળ પણ વેગ શૂન્ય હોય.
ઉકેલ:
અમુક ઊંચાઈએથી મુક્ત પતન કરતો પદાર્થ
(મુક્ત પતન કરતા પદાર્થનો પ્રારંભિક વેગ (u) શૂન્ય હોય છે, પણ તેનો પ્રવેગ 9.8m/s² જેટલો અચળ હોય છે.)

(b) કોઈ પદાર્થ કે જે નિશ્ચિત દિશામાં ગતિ કરતો હોય તથા તેનો પ્રવેગ લંબ દિશામાં હોય. [3 ગુણ)
ઉકેલ:
નિયમિત વર્તુળમય ગતિ કરતો પદાર્થ
(નિયમિત વર્તુળમય ગતિ કરતા પદાર્થના કિસ્સામાં વર્તુળમાર્ગના જે-તે બિંદુ આગળ પદાર્થનો વેગ ત્યાં દોરેલ સ્પર્શકની દિશામાં હોય છે, પણ તેનો પ્રવેગ કેન્દ્રગામી (વર્તુળના કેન્દ્ર તરફની દિશામાં) હોય છે; અર્થાત્ પદાર્થનો વેગ અને પ્રવેશ પરસ્પર લંબ હોય છે.)

પ્રશ્ન 10.
એક કૃત્રિમ ઉપગ્રહ 42,250 km ત્રિજ્યાની વર્તુળાકાર કક્ષામાં પરિભ્રમણ કરે છે. જો તે 24 કલાકમાં પૃથ્વીનું પરિક્રમણ કરતો હોય તો તેની ઝડપ ગણો.
ઉકેલ:
અહીં, ત્રિજ્યા r = 42250 km
= 42250 × 1000 m
1 પરિક્રમણ પૂર્ણ કરવા લાગતો સમય (એટલે આવર્તકાળ)
= 24 h = 24 × 60 × 60 s

= 3073.74 m s^-1 (અથવા 3.07374 km s^-1)

→ ઉપગ્રહની ઝડપ ની ગણતરી km/hમાં નીચે મુજબ થાયઃ
= 3073.74 × \(\frac{10^{-3} \mathrm{~km}}{\left(\frac{1}{3600}\right) \mathrm{h}}\)
= \(\frac{(3073.74 \times 3600) \times 10^{-3}}{1}\) × 10 km h^-1
= 11065464 × 10-3 km h^-1
= 11065.464 km h^-1
= 1.11 × 104 km h^-1

GSEB Class 9 Science ગતિ Intext Questions and Answers

Intext પ્રશ્નોત્તર [પા.પુ. પાના નં. 100]

પ્રશ્ન 1.
કોઈ પદાર્થ દ્વારા કંઈક અંતર કપાયેલ છે. શું તેનું સ્થાનાંતર શૂન્ય હોઈ શકે? જો હા, તો આપના ઉત્તરને ઉદાહરણ દ્વારા સમજાવો.
ઉત્તર:
હા. પદાર્થનું સ્થાનાંતર શૂન્ય હોઈ શકે છે.
ઉપરોક્ત હકીકત ત્યારે જ શક્ય બને છે કે જ્યારે પદાર્થના ગતિપથનું પ્રારંભિક સ્થાન અને અંતિમ સ્થાન એક જ હોય.

ઉદાહરણ: એક વિદ્યાર્થી પોતાના ઘરેથી ચાલીને સ્કૂલે જાય છે અને ત્યાંથી પાછો ફરીને પોતાના ઘરે આવે છે.
તો વિદ્યાર્થીએ કેટલુંક અંતર કાપ્યું હશે પણ તેનું સ્થાનાંતર શૂન્ય હશે.

પ્રશ્ન 2.
એક ખેડૂત 10 m લંબાઈના એક ચોરસ ખેતરની ધારે ધારે 40 sમાં એક ચક્કર પૂર્ણ કરે છે. 2 મિનિટ 20 સેકન્ડ બાદ 3 આ ખેડૂતે પ્રારંભિક સ્થાનથી કેટલું સ્થાનાંતર કર્યું હશે?
ઉત્તર:

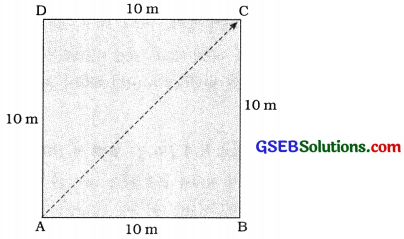
[આકૃતિ 8.5 ચોરસ ખેતર].

અહીં, ચોરસ ખેતરની સરહદ પર ચાલીને 1 પરિક્રમણના અંતે ખેડૂતે કાપેલું અંતર = ચોરસની પરિમિતિ
= 4 × 10 m
= 40 m
હવે, 1 પરિક્રમણ પૂર્ણ કરવા માટે એટલે કે 40 m અંતર કાપવા માટે ખેડૂતને લાગતો સમય = 40 s
∴ 2 મિનિટ અને 20 સેકન્ડમાં એટલે કે 140 sમાં ખેડૂત દ્વારા કપાતું અંતર = 140 m
હવે, 40 m = 1 પરિક્રમણ
∴ 140 m = \(\frac{140}{40}\) પરિક્રમણ = 3.5 પરિક્રમણ
0.5 પરિક્રમણ = 0.5 × 40 m = 20 m
તેથી આકૃતિ 8.5માં દર્શાવ્યા પ્રમાણે ખેડૂતનું પ્રારંભિક સ્થાન A છે. તેથી 2 મિનિટ અને 20 સેકન્ડના અંતે તેનું અંતિમ સ્થાન C હશે.
∴ ખેડૂતનું સ્થાનાંતર = AC
સ્થાનાંતરનું મૂલ્ય શોધવા માટે કાટકોણ ∆ ABC માટે પાયથાગોરસનો પ્રમેય વાપરતાં,
AC² = AB² + BC²
= (10)² + (10)² = 100 + 100 = 200 m
∴ AC = 200 m
= \(\sqrt{100 \times 2}\) m
= 10 √2 m
∴ ખેડૂતનું સ્થાનાંતર 10 √2 m

પ્રશ્ન 3.
સ્થાનાંતર માટે નીચેના પૈકી કયું સાચું છે?
(a) તે શૂન્ય હોઈ શકે નહિ.
ઉત્તર:
ખોટું. સ્થાનાંતર શૂન્ય હોઈ શકે છે.

(b) તેનું મૂલ્ય પદાર્થ દ્વારા પાયેલ અંતર કરતાં વધુ હોય છે.
ઉત્તર:
ખોટું. સ્થાનાંતરનું મૂલ્ય કપાયેલ અંતર જેટલું અથવા તેનાથી ઓછું હોય છે.

Intext પ્રશ્નોત્તર [પા.પુ. પાના નં. 102]

પ્રશ્ન 1.
ઝડપ અને વેગ વચ્ચેનો ભેદ સ્પષ્ટ કરો.
ઉત્તરઃ

પ્રશ્ન 2.
કઈ પરિસ્થિતિમાં પદાર્થના સરેરાશ વેગ અને સરેરાશ ઝડપનાં મૂલ્યો સમાન થાય?
ઉત્તર:
જ્યારે પદાર્થ સુરેખ પથ પર એક જ દિશામાં ગતિ કરે છે ત્યારે તેના સરેરાશ વેગ અને સરેરાશ ઝડપનાં મૂલ્યો સમાન થાય.

પ્રશ્ન 3.
વાહનનું ઓડોમિટર શું માપે છે?
ઉત્તર:
વાહનનું ઓડોમિટર વાહને કાપેલું અંતર માપે છે.

પ્રશ્ન 4.
જ્યારે કોઈ પદાર્થ નિયમિત ગતિ કરતો હોય ત્યારે તેનો ગતિપથ કેવો દેખાશે?
ઉત્તર:
પદાર્થનો ગતિપથ સુરેખ હશે.

પ્રશ્ન 5.
એક પ્રયોગ દરમિયાન અવકાશયાનમાંથી એક સિગ્નલને પૃથ્વી પરના સ્ટેશન સુધી પહોંચતાં 5 min જેટલો સમય લાગે છે. પૃથ્વી પરના સ્ટેશનથી અવકાશયાનનું અંતર કેટલું હશે? સિગ્નલનો વેગ પ્રકાશના વેગ જેટલો જ એટલે કે ૩× 10⁸ m s^-1 છે.
ઉકેલ:
સમય t = 5 minute = 5 × 60 s = 300 s
સિગ્નલનો વેગ D = 3 × 10⁸m s^-1
પૃથ્વી પરના સ્ટેશનથી અવકાશયાનનું અંતર = = ?
વેગ =
∴ અંતર = વેગ × સમય
= 3 × 10⁸ × 300
= 900 × 10⁸ m
= 9 × 10¹⁰ m
આમ, અવકાશયાનનું પૃથ્વી પરના સ્ટેશનથી અંતર 9 × 10¹⁰m છે.

Intext પ્રબોત્તર [પા.પુ. પાના નં. 103]

પ્રશ્ન 1.
તમે કોઈ વસ્તુની બાબતમાં ક્યારે કહી શકો કે,
(i) તે અચળ પ્રવેગથી ગતિ કરે છે?
ઉત્તર:
જ્યારે પદાર્થ સુરેખ પથ પર ગતિ કરતો હોય અને એકસરખા સમયગાળામાં તેનો વેગ એકસરખા પ્રમાણમાં વધતો હોય, તો પદાર્થ અચળ પ્રવેગી કે નિયમિત પ્રવેગી ગતિ કરે છે તેમ કહેવાય.

(ii) તે અસમાન પ્રવેગથી ગતિ કરે છે?
ઉત્તર:
જ્યારે પદાર્થનો વેગ એકસરખા સમયગાળામાં જુદા જુદા પ્રમાણમાં બદલાતો હોય, તો પદાર્થનો પ્રવેગ અનિયમિત છે તેમ કહેવાય.

પ્રશ્ન 2.
એક બસની ગતિ 5 sમાં 80 km h^-1થી ઘટીને 60 km h^-1 થઈ જાય છે. બસનો પ્રવેગ શોધો.
ઉકેલ:
બસની પ્રારંભિક ઝડપ u = 80 km h^-1
= \(\frac{80 \times 1000 \mathrm{~m}}{60 \times 60 \mathrm{~s}}\)
= \(\frac{800}{36}\) m s^-1

બસની અંતિમ ઝડપ b = 60 km h^-1
= \(\frac{60 \times 1000 \mathrm{~m}}{60 \times 60 \mathrm{~s}}\)
= \(\frac{600}{36}\) m s^-1
સમય t = 5 s
પ્રવેગ વ = \(\frac{v-u}{t}\)
= \(\frac{\frac{600}{36}-\frac{800}{36}}{5}\)
= \(\frac{-200}{36} \times \frac{1}{5}\)
= – \(\frac{10}{9}\) ≈ -1.11 m s^-2

પ્રશ્ન 3.
એક ટ્રેન રેલવે સ્ટેશનથી ગતિનો પ્રારંભ કરે છે અને અચળ પ્રવેગથી ગતિ કરી 10 minમાં 40 km h^-1ની ઝડપ પ્રાપ્ત કરે છે, તો તેનો પ્રવેગ શોધો.
ઉકેલ:
પ્રારંભિક ઝડપ u = 0 m s^-1
અંતિમ ઝડપ b = 40 km h^-1
= \(\frac{40 \times 1000}{3600}\)
= \(\frac{100}{9}\) m s^-1
પ્રવેગ વ = \(\frac{v-u}{t}\)
= \(\frac{\frac{100}{9}-0}{600}\)
= \(\frac{100}{9 \times 600}\)
= \(\frac{1}{54}\) m s^-2
= 1.85 × 10^-2 m s^-2

Intext પ્રશ્નોત્તર [પા.પુ. પાના નં. 107].

પ્રશ્ન 1.
કોઈ પદાર્થની નિયમિત અને અનિયમિત ગતિ માટે અંતર – સમયના આલેખનો આકાર કેવો હોય છે?
ઉત્તર:
નિયમિત ગતિ માટે અંતર – સમયનો આલેખ સુરેખા હોય છે, જે સમય-અક્ષ (X-અક્ષ) સાથે ઢળતો હોય છે, અર્થાત્ આલેખના ઢાળનું કંઈક મૂલ્ય (શૂન્ય અને અનંત નહિ) હોય છે.
અનિયમિત ગતિ માટે અંતર – સમયનો આલેખ સુરેખ હોતો નથી.

પ્રશ્ન 2.
કોઈ પદાર્થની ગતિની બાબતમાં તમે શું કહી શકો જેનો અંતર – સમયનો આલેખ સમયની અક્ષને સમાંતર રેખા હોય?
ઉત્તર:
તે પદાર્થ સ્થિર હશે, કારણ કે સમયની દરેક ક્ષણે પદાર્થનું અંતર બદલાતું નથી.

પ્રશ્ન 3.
કોઈ પદાર્થની ગતિની બાબતમાં તમે શું કહી શકો જેનો ઝડપ – સમયનો આલેખ સમયની અક્ષને સમાંતર રેખા હોય?
ઉત્તર:
પદાર્થ અચળ ઝડપે ગતિ કરતો હશે, કારણ કે સમયના દરેક ક્ષણે પદાર્થની ઝડપ બદલાતી નથી.

પ્રશ્ન 4.
વેગ – સમયના આલેખની નીચે ઘેરાયેલ ક્ષેત્રફળનું માપ કઈ ભૌતિક રાશિ દર્શાવે છે?
ઉત્તરઃ
આપેલ સમયગાળામાં પદાર્થના સ્થાનાંતરનું મૂલ્ય દર્શાવે છે. જો પદાર્થ સુરેખ પથ પર એક જ દિશામાં ગતિ કરતો હોય, તો તે પદાર્થ દ્વારા કપાયેલું અંતર સૂચવે છે.

Intext પ્રશ્નોત્તર [પા.પુ. પાના નં. 109]

પ્રશ્ન 1.
એક બસ સ્થિર સ્થિતિમાંથી ગતિની શરૂઆત કરે છે તથા 2 min સુધી 0.1 m s^-2ના અચળ પ્રવેગથી ગતિ કરે છે, તો
(a) પ્રાપ્ત કરેલ ઝડપ અને
(b) તેણે કાપેલ અંતર શોધો.
ઉકેલ:
અહીં, u = 0; a = 0.1 m s^-2;
t = 2 minute = 120 s, v = ?, s = ?

(a) v = u + at
= 0 + (0.1 m s^-2) × (120 s)
= 12 m s^-1

(b) s = ut + \(\frac{1}{2}\)at²
= (0) × (120 s) + \(\frac{1}{2}\) × (0.1 m s^-2) × (120 s)²
= \(\frac{1}{2}\) × 0.1 × 120 × 120
= 720 m
આમ, બસે પ્રાપ્ત કરેલ ઝડપ 12 m s^-1 અને બસે કાપેલ અંતર 720 m.

પ્રશ્ન 2.
એક ટ્રેન 90 km/h^-1ની ઝડપથી ગતિ કરી રહી છે. બ્રેક મારતાં તેમાં – 0.5 m s^-2નો અચળ પ્રવેગ ઉત્પન્ન થાય છે. ટ્રેન સ્થિર સ્થિતિમાં આવે તે પહેલાં કેટલું અંતર કાપશે?
ઉકેલ:
અહીં, u = 90 km h^-1
= \(\frac{90 \times 1000 \mathrm{~m}}{3600 \mathrm{~s}}\) = 25 m s^-1
a = – 0.5 m s^-2
v = 0 (∵ ટ્રેન અંતે સ્થિર થાય છે.)
હવે, v² – u² = 2as
∴ 0 – (25 m s^-1)² = 2 × (- 0.5 m s^-2) × s
∴ s = \(\frac{-(25 \times 25)}{-2 \times 0.5}\) = 625 m
આમ, ટ્રેન સ્થિર સ્થિતિમાં આવે તે પહેલાં 625 m અંતર કાપશે.

પ્રશ્ન 3.
એક રૅલી ઢોળાવ ધરાવતી સપાટી પર 2 ms^-2ના પ્રવેગથી નીચે તરફ ગતિ કરી રહી છે. ગતિની શરૂઆત બાદ 3 sના અંતે તેનો વેગ કેટલો હશે?
ઉકેલઃ
અત્રે, u = 0; a = 2 cm s^-2; t = 3 s; v = ?
v = u + at
= 0 + (2 cm s^-2) × (3 s) = 6 cm s^-1
આમ, ટ્રૉલી સ્થિર સ્થિતિમાંથી ઢોળાવ પરથી નીચે તરફ ગતિ કરે ત્યારે 3 sના અંતે તેનો વેગ 6 cm s^-1 હશે.

પ્રશ્ન 4.
એક રેસિંગ કારનો અચળ પ્રવેગ 4 ms છે. ગતિની શરૂઆત બાદ 10 sના અંતે તેણે કેટલું અંતર કાપેલ હશે?
ઉકેલઃ
અત્રે, u = 0; a = 4m s^-2; t = 10 s
s = ut + \(\frac{1}{2}\)at²
= 0 × (10 s) + \(\frac{1}{2}\)(4 m s^-2) × (10 s)²
= 2 × 100
= 200 m
આમ, રેસિંગ કારે સ્થિર સ્થિતિમાંથી ગતિની શરૂઆત કર્યા બાદ 10 sના અંતે 200 m અંતર કાપેલ હશે.

પ્રશ્ન 5.
એક પથ્થરને ઊર્ધ્વદિશામાં 5m s^-1ના વેગથી ફેંકવામાં આવે છે. જો ગતિ દરમિયાન પથ્થરનો અધોદિશામાં પ્રવેગ 10 m s^-2 હોય, તો પથ્થર કેટલી ઊંચાઈ પ્રાપ્ત કરશે તથા તેને ત્યાં પહોંચતાં કેટલો સમય લાગશે?
ઉકેલ:
અહીં, u = 5 m s^-1;
a = – 10 m s^-2 (∵ પથ્થર શિરોલંબ ઊર્ધ્વદિશામાં ગતિ કરે છે.)
મહત્તમ ઊંચાઈએ v = 0
હવે, v = u + at
∴ 0 = (5 m s^-1) + (- 10 m s^-2)t
∴10t = 5.
∴ t = 0.5 s
હવે, v² – u² = 2as
∴ (0)² – (5 m s^-1)² = 2(- 10 m s^{– 2}) × s
∴ – 25 = – 20 s
∴ s = \(\frac{25}{20}\) = 1.25 m
આમ, પથ્થર 1.25 m જેટલી મહત્તમ ઊંચાઈ પ્રાપ્ત કરશે અને ત્યાં પહોંચવા માટે 0.5 s જેટલો સમય લેશે.

GSEB Class 9 Science ગતિ Textbook Activities

પ્રવૃત્તિ 8.1 [પા.પુ. પાના નં. 98]

• તમારા ક્લાસરૂમની દીવાલો સ્થિર અવસ્થામાં છે કે ગતિમાં છે તેની ચર્ચા કરો.

ચર્ચા-વિચારણા વર્ગખંડની દીવાલો તેની આસપાસનાં બીજાં ૨ મકાનોની સાપેક્ષે સ્થિર છે, તે પૃથ્વીની પોતાની ગતિનો એક હિસ્સો છે, પરંતુ જો પૃથ્વીની બહારથી (અવકાશમાંથી) વર્ગખંડની દીવાલો જોવામાં આવે તો તે ગતિમાન લાગે છે.

નિષ્કર્ષઃ કોઈ પણ પદાર્થની સ્થિર અવસ્થા અને ગતિમાન અવસ્થા નિરપેક્ષ નથી પણ સાપેક્ષ છે.

પ્રવૃત્તિ 8.2 પા.પુ. પાના નં. 98].

• શું તમે ક્યારેય એવો અનુભવ કર્યો છે કે જે ટ્રેનમાં તમે બેઠા છો તે ગતિ કરતી પ્રતીત થાય પરંતુ વાસ્તવમાં તે સ્થિર હોય? આ બાબત પર ચર્ચા કરો અને તમારા વિચારોનું આદાન-પ્રદાન કરો.

ચર્ચા-વિચારણા: હા જ્યારે આપણે સ્થિર ટ્રેનમાં બેઠા હોઈએ અને કોઈ બીજી ટ્રેન પાસેના નજીકના) પાટા પરથી ઝડપથી ગતિ કરતી જાય, તો આપણને આપણી ટ્રેન વિરુદ્ધ દિશામાં ગતિ કરતી જણાય છે.

નિષ્કર્ષ: ટ્રેનની કે કોઈ પદાર્થની સ્થિર અવસ્થા અને ગતિમાન 3 અવસ્થા બંને સાપેક્ષ છે.

વિચારો અને વર્તો:

આપણે ક્યારેક આપણી આસપાસના પદાર્થોની ગતિને કારણે તકલીફમાં મુકાઈએ છીએ. ખાસ કરીને જો તે પદાર્થની ગતિ અનિશ્ચિત અને અનિયંત્રિત હોય જેમ કે નદીમાં આવેલ પૂર, તોફાન કે ત્સુનામી. જ્યારે બીજી બાજુ પદાર્થની નિયંત્રિત ગતિ માનવની સેવામાં ઉપયોગી થઈ પડે છે. જેમ કે, પાણી દ્વારા વિદ્યુતનું ઉત્પાદન. શું તમે એ અનુભવો છો કે કેટલાક પદાર્થોની અનિયમિત ગતિનો અભ્યાસ કરવો અને તેને નિયંત્રિત કરવા અંગેનો અભ્યાસ જરૂરી છે?

હા. પૂર, વાવાઝોડું, સુનામી, જ્વાળામુખીનું ફાટવું વગેરે વિનાશક હોનારતો માનવજાત પર ઘણી અસર કરે છે. આ વિનાશક હોનારતોનું અનુમાન કદાચ કરી શકાય છે પણ તેમને નિયંત્રિત/અંકુશિત કરી શકાતી નથી.

→ ભૌતિક વિજ્ઞાનની શાખા ઇલેક્ટ્રોનિક્સમાં ઓરડાના તાપમાને અર્ધવાહકોમાં થતી ઈલેક્ટ્રૉન્સ અને હૉલ(કાલ્પનિક ધન વિદ્યુતભારિત કણ)ની અનિશ્ચિત, અસ્તવ્યસ્ત અને અનિયંત્રિત ગતિને યોગ્ય રીતે નિયંત્રિત કરવામાં આવે છે અને તેના લીધે આપણે ઘણાં બધાં ઇલેક્ટ્રૉનિક ઉપકરણો/સાધનો બનાવી શક્યા છીએ.

→ ન્યુક્લિયર પાવર-પ્લાન્ટમાં ન્યૂટ્રૉન્સની અનિશ્ચિત અને અનિયંત્રિત ગતિને નિયંત્રિત કરીને સફળ નિયંત્રિત શૃંખલા પ્રક્રિયા ઉપજાવવામાં આવે છે અને મોટા પ્રમાણમાં વિદ્યુતઊર્જા ઉત્પન્ન કરવામાં આવે છે.

→ ગતિ કરતાં ઉપગ્રહો, હવામાનની તરાહ, રાસાયણિક પ્રક્રિયાઓ વગેરે અનિયંત્રિત અને અનિશ્ચિત ગતિ દર્શાવતાં ઉદાહરણો છે. આપણે આવાં વિવિધ તંત્રોનો ઊંડાણપૂર્વક અભ્યાસ કરવો જોઈએ અને તેમને નાના પાયે પણ નિયંત્રિત કરવાનો પ્રયત્ન કરવો જોઈએ.

પ્રવૃત્તિ 8.3 [પા.પુ. પાના નં 99]

→ એક મીટરપટ્ટી અને એક લાંબું દોરડું લો.
→ બાસ્કેટબૉલના મેદાનના એક ખૂણાથી તેની વિરુદ્ધ આવેલા બીજા ખૂણા સુધી તેની ધારે ધારે ચાલતાં જાઓ.
→ તમારા દ્વારા કરાયેલ અંતર અને સ્થાનાંતરનું મૂલ્ય માપો.

• આ કિસ્સામાં બંને વચ્ચે તમે શું તફાવત નોંધો છો?

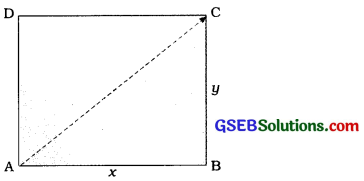
[આકૃતિ 8.4: બાસ્કેટબૉલનું મેદાન]

ચર્ચા-વિચારણા બાસ્કેટબૉલના મેદાનના એક ખૂણા Aથી સામેના ખૂણા C સુધી તેની સંલગ્ન બાજુઓ AB અને BC પર ચાલીને કાપેલું અંતર = Aથી B અને Bથી C
= AB + BC = x + y
અને સ્થાનાંતર = Aથી C
= AC = \(\sqrt{x^{2}+y^{2}}\) (∵ આકૃતિ 8.4 પરથી)
∴ AC < AB + BC
અહીં, સ્થાનાંતરનું મૂલ્ય, અંતર કરતાં ઓછું છે.
નિષ્કર્ષ: અંતર એટલે પદાર્થે કરેલ મુસાફરીની સાચી પથલંબાઈ, જ્યારે સ્થાનાંતર એટલે પ્રારંભિક સ્થાનથી અંતિમ સ્થાન સુધીનું લઘુતમ અંતર.

પ્રવૃત્તિ 8.4 [પા.પુ. પાના નં. 99].

→ ગાડીમાં એક એવું સાધન ફિટ કરેલ હોય છે કે જેના દ્વારા તેણે કાપેલ અંતર જાણી શકાય છે. આ સાધનને ઓડોમિટર કહે છે. એક કારને ભુવનેશ્વરથી નવી દિલ્લી સુધી લઈ જવામાં આવે છે. ઓડોમિટરના અંતિમ વાંચન અને પ્રારંભિક વાંચન વચ્ચેનો તફાવત 1850 km છે.

→ ભારતના રોડ નકશાનો ઉપયોગ કરી ભુવનેશ્વર અને નવી દિલ્લી વચ્ચેનું સ્થાનાંતર ગણી તેની નોંધ કરો.
અવલોકન: કારમાં લગાડેલું ઓડોમિટર ભુવનેશ્વર અને નવી દિલ્લી વચ્ચેનું કારે કાપેલું ખરેખરું અંતર દર્શાવે છે, જે 1850 km માલૂમ પડેલું છે.

ભારતના માર્ગ-નકશા પર ભુવનેશ્વર અને નવી દિલ્લીનું સૌપ્રથમ ચોક્કસ સ્થાન દર્શાવવું. માપપટ્ટીની મદદથી માર્ગ-નકશા પર ભુવનેશ્વર અને નવી દિલ્લી વચ્ચેની સુરેખ લંબાઈ માપવી. માર્ગ-નકશા પર આપેલ અંતર માટેના સ્કેલમાપનો ઉપયોગ કરીને અર્થાત્ માપેલી લંબાઈને અંતરના સ્કેલ વડે ગુણીને સ્થાનાંતરનું મૂલ્ય શોધો, જે આશરે 1270 km મળે છે. (બંને શહેરો વચ્ચેના સ્થાનાંતરનું મૂલ્ય બંને શહેરો વચ્ચેના હવાઈ અંતરનું માપન કરીને પણ મેળવી શકાય છે.)
અહીં, કારના સ્થાનાંતરનું મૂલ્ય, તેણે ખરેખર કાપેલ અંતર કરતાં ઓછું મળે છે.

નિષ્કર્ષ: અત્રે સાચી પથલંબાઈ, સ્થાનાંતરના મૂલ્ય કરતાં વધુ મળે છે.

પ્રવૃત્તિ 8.5 [પા.પુ. પાના નં. 100]

→ બે પદાર્થો A તથા Bની ગતિ સાથે સંબંધિત માહિતી કોષ્ટક 8.1માં આપેલ છે.
→ ધ્યાનથી ચકાસો અને બતાવો કે પદાર્થોની ગતિ નિયમિત (સમાન) છે કે અનિયમિત (અસમાન).

કોષ્ટક 8.1

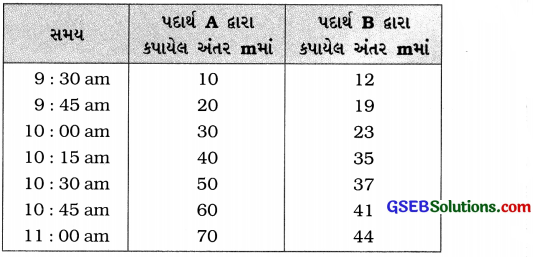
ચર્ચા-વિચારણા: કોષ્ટક 8.1 પરથી સ્પષ્ટ છે કે એકસરખા સમયગાળા(= 15 minute)માં પદાર્થ A એકસરખું અંતર (= 10 m) કાપે છે, પણ પદાર્થ કે જુદાં જુદાં અંતર કાપે છે. માટે પદાર્થ A નિયમિત ગતિ અને પદાર્થ B અનિયમિત ગતિ કરે છે.

નિષ્કર્ષ: આ પ્રવૃત્તિ નિયમિત ગતિ અને અનિયમિત ગતિ વચ્ચેનો મૂળ તફાવત સમજાવે છે.

પ્રવૃત્તિ 8.6 [પા.પુ. પાના નં. 101]

• તમે તમારા ઘરેથી બસ-સ્ટેન્ડ કે શાળા સુધી ચાલીને જતાં લાગતો સમય નોંધો. જો તમારી ચાલવાની સરેરાશ ઝડપ 4 km h^-1 લેવામાં આવે, તો બસ-સ્ટેન્ડ કે શાળાનું અંતર તમારા ઘરથી નક્કી કરો.

અવલોકન: ધારો કે, ઘરેથી બસ-સ્ટૅન્ડ સુધી અથવા શાળા સુધી ચાલીને જવા માટે લાગતો સમય 15 minute છે.
15 minute = 15 × 60 = 900 s
અહીં, ધારેલી સરેરાશ ઝડપ 4 km h^-1
= \(\frac{4 \times 1000 \mathrm{~m}}{60 \times 60 \mathrm{~s}}\) = \(\frac{40}{36}\) m/s = \(\frac{20}{18}\) m s^-1
હવે, સરેરાશ ઝડપ =
∴ કુલ અંતર = સરેરાશ ઝડપ ૪ કુલ સમય
= (\(\frac{20}{18}\) m s^-1) × 900 s)
= 1000 m
= 1 km

નિષ્કર્ષ: ઘર અને બસ-સ્ટેન્ડ અથવા શાળા વચ્ચેનું આ અંતર એ અંદાજિત અંતર છે, કારણ કે સરેરાશ ઝડપ અને કુલ સમય બને ચોક્કસ નથી.

પ્રવૃત્તિ 8.7 [પા.પુ. પાના નં 102]

• જ્યારે આકાશ વાદળોથી ઘેરાયેલું હોય ત્યારે વીજળી ચમકવાની અને વાદળોના ગડગડાટની ઘટના વારંવાર થતી જોવા મળે છે. આ ઘટનામાં વીજળીનો ચમકારો પહેલાં દેખાય છે. તેના થોડા સમય છે પછી વાદળોના ગડગડાટનો ધ્વનિ આપણા સુધી પહોંચે છે.
  શું તમે સમજાવી શકો કે આવું કેમ થાય છે?
• આ બંને ઘટનાઓ વચ્ચેનો સમયગાળો ડિજિટલ કાંડા ઘડિયાળ કે સ્ટૉપવૉચની મદદથી માપો.
• વીજળીના ચમકારાના સૌથી નજીકના બિંદુનું અંતર ગણો.
  (હવામાં ધ્વનિની ઝડપ 346 m s^-1 છે.)

અવલોકન: આકાશી વીજળીના પ્રકાશની ઝડપ 3 × 10 m s^-1 છે. જ્યારે ઉદ્ભવતા ધ્વનિની ઝડપ 346 m s^-1 છે. આમ, વીજળીના પ્રકાશની ઝડપ ધ્વનિની ઝડપ કરતાં ખૂબ વધારે હોવાથી આપણને આકાશી વીજળી પહેલાં દશ્યમાન થાય છે અને થોડા સમય બાદ વાદળોના ગડગડાટનો ધ્વનિ સંભળાય છે. (બંને ભલેને એકસાથે ઉત્પન્ન થતા હોય.)

→ ડિજિટલ કાંડા-ઘડિયાળ અથવા સ્ટૉપવૉચ વડે માપેલો આ સમયગાળો
2 second છે. (અર્થાત્ વીજળીનો પ્રકાશ દેખાય ત્યારબાદ
2 second પછી વાદળોના ગડગડાટનો ધ્વનિ સંભળાય છે.)

→ આપણી સૌથી નજીક થતી આકાશી વીજળીનું અંતર = ઝડપ × સમય
∴ અંતર = 346 m s^-1 × 2s = 692 m

નોંધઃ આપણી સૌથી નજીક થતી આકાશી વીજળીનું અંતર ગણવા માટે અહીં ધ્વનિની ઝડપ ધ્યાનમાં લીધી છે અને તેને સમયગાળા વડે ગુણેલ છે, કારણ કે પ્રકાશની ઝડપ લગભગ અનંત છે (ધ્વનિની સાપેક્ષે). આથી પ્રકાશ આપણી પાસે પહોંચવા માટે નહિવત્ સમય લે છે.

→ અત્રે માપેલો સમયગાળો એ વાદળોના ગડગડાટના ધ્વનિને આપણી પાસે પહોંચવા માટેનો છે.
નિષ્કર્ષ: પ્રકાશની ઝડપ, ધ્વનિની ઝડપ કરતાં વધુ હોય છે.

પ્રવૃત્તિ 8.8 [પા.પુ. પાના નં. 103]

→ તમે રોજિંદા જીવનમાં ઘણા પ્રકારની ગતિ અનુભવો છો. જેવી કે,
(a) પ્રવેગ ગતિની દિશામાં હોય.
(b) પ્રવેગ ગતિની વિરુદ્ધ દિશામાં હોય.
(c) પ્રવેગ અચળ હોય.
(d) પ્રવેગ અસમાન હોય.

→ શું તમે ઉપર દર્શાવેલ દરેક પ્રકારની ગતિનું એક-એક ઉદાહરણ આપી શકશો?

અવલોકન: હા.
(a) સુરેખ રસ્તા પર ગતિ કરતા વાહનની ઝડપ વધતી હોય ત્યારે તેનો પ્રવેગ તેની ગતિની દિશામાં હોય છે.
(b) જ્યારે સુરેખ રસ્તા પર ગતિ કરતા વાહન પર બ્રેક લગાડવામાં આવે ત્યારે વાહનની ઝડપ ઘટતી જશે. આ વખતે વાહનમાં ઉત્પન્ન થતો પ્રવેગ તેની ગતિની વિરુદ્ધ દિશામાં હોય છે.
(c) અમુક ઊંચાઈએથી મુક્ત પતન કરતા પદાર્થની ગતિ અચળ પ્રવેગી ગતિ છે. પદાર્થનો પ્રવેગ, 9 = 9.8 m s^-2 જેટલો અચળ હોય છે.
(d) ટ્રાફિકવાળા રસ્તા પર થતી વાહનની ગતિ જે અનિયમિત પ્રવેગી પ્રતિપ્રવેગી હોય છે.

પ્રવૃત્તિ 8.9 [પા.પુ. પાના નં. 106]

• એક ટ્રેનના ત્રણ સ્ટેશનો A, B અને C પરના આગમન અને પ્રસ્થાનના સમય તથા સ્ટેશન B અને Cના સ્ટેશન Aથી અંતર કોષ્ટક 8.4માં દર્શાવેલ છે.

કોષ્ટક 8.4: સ્ટેશન B અને Cનાં Aથી અંતરો તથા ટ્રેનનો આવવાનો અને જવાનો સમય

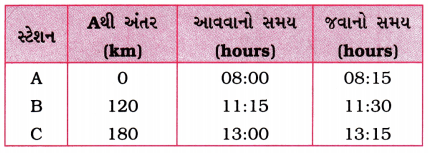
• કોઈ બે સ્ટેશનોની વચ્ચે ટ્રેનની ગતિ અચળ છે તેમ સ્વીકારી લઈને વેગ – સમયનો આલેખ દોરો અને તેનું અર્થઘટન કરો.

ચર્ચા-વિચારણા ટ્રેન માટે અંતર – સમયનો આલેખ આકૃતિ 8.16માં દર્શાવ્યો છે.
→ 8: 00થી 8: 15 સુધી ટ્રેન સ્ટેશન A ઉપર ઊભેલી છે. સ્ટેશન A ઊગમબિંદુ ‘O’ પર લીધેલ છે.
→ 8: 15થી 11: 15 સુધી ટ્રેન અચળ ઝડપે ગતિ કરીને અર્થાત્ નિયમિત ગતિ કરીને B સ્ટેશને પહોંચે છે, જે સ્ટેશન Aથી 120 km અંતરે છે.
→ 11: 15થી 11:30 સુધી ટ્રેન સ્ટેશન B પર ઊભી રહે છે.
→ 11: 30થી 13: 00 સુધી ટ્રેન અચળ ઝડપે ગતિ કરીને અર્થાત્ નિયમિત ગતિ કરીને C સ્ટેશને (180 – 120) = 60 km અંતર કાપીને પહોંચે છે.
→ 13: 00થી 13: 15 સુધી ટ્રેન સ્ટેશન C પર ઊભી રહે છે.

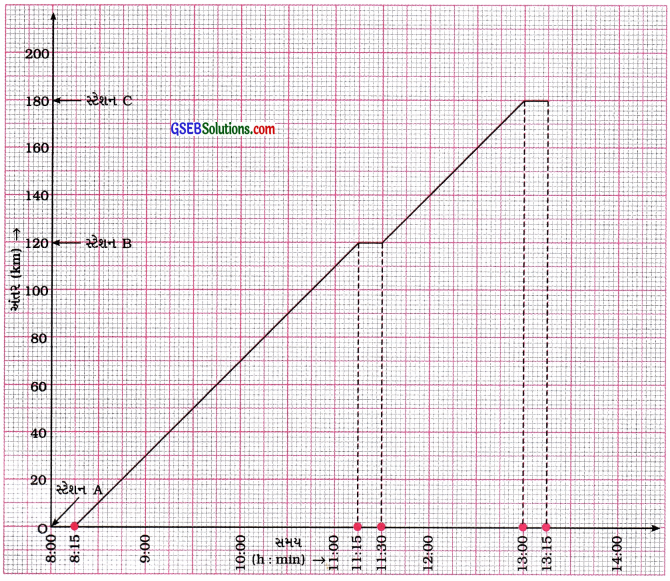
[આકૃતિ 8.16: ટ્રેન માટે અંતર – સમયનો આલેખ]

→ અહીં સ્ટેશન Aથી B સુધીનું 120 km અંતર ટ્રેન 3 hમાં કાપે છે. તેથી A અને B સ્ટેશન વચ્ચે તેની ઝડપ υ₁ = \(\frac{120}{3}\) = 40 km h^-1.
→ સ્ટેશન Bથી C સુધીનું 60 km અંતર ટ્રેન 1h અને 30 minuteમાં કાપે છે. તેથી B અને C વચ્ચે તેની ઝડપ υ₂ = \(\frac{60 \mathrm{~km}}{1.5 \mathrm{~h}}\) = 40 km h^-1.
→ અત્રે આલેખના બે વિભાગોના ઢાળ સમાન મળે છે.

નિષ્કર્ષ : જ્યારે ગતિ નિયમિત હોય છે ત્યારે અંતર – સમયનો આલેખ સુરેખ હોય છે અને આ સુરેખાનો ઢાળ પદાર્થનો વેગ દર્શાવે છે, કારણ કે પદાર્થ સુરેખ પથ પર એક જ દિશામાં અચળ ઝડપે ગતિ કરે છે.

પ્રવૃત્તિ 8.10 [પા.પુ. પાના નં. 107]

• ફિરોઝ અને તેની બહેન સાનિયા તેમની સાઇકલો પર શાળાએ જાય છે. તે બંને ઘરેથી એકસાથે પ્રસ્થાન કરે છે તેમજ એક જ માર્ગે ગતિ કરે છે; છતાં અલગ અલગ સમયે શાળાએ પહોંચે છે. કોષ્ટક 8.5માં બંને દ્વારા અલગ અલગ સમય પર કાપેલ અંતર દર્શાવેલ છે.

કોષ્ટક 8.5: ફિરોઝ અને સાનિયા દ્વારા જુદા જુદા સમયમાં તેમની સાઈકલો વડે કપાયેલ અંતર

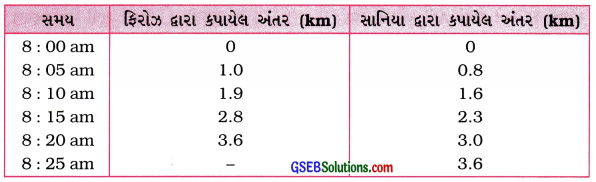
• આ બંનેની ગતિ માટે અંતર – સમયનો આલેખ એક જ સ્કેલ પર દોરો અને તેનું અર્થઘટન કરો.

ચર્ચા-વિચારણા: યોગ્ય સ્કેલમાપ લઈને ફિરોઝ અને સાનિયા માટે અંતર – સમયના આલેખ આકૃતિ 8.17માં દર્શાવ્યા છે.

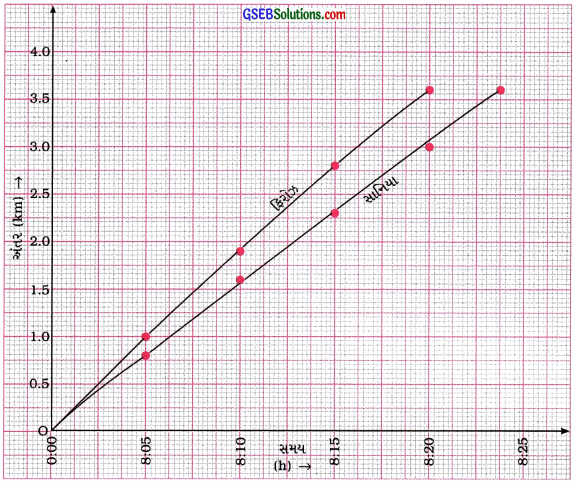
[આકૃતિ 8.17: ફિરોઝ અને સાનિયા માટે અંતર – સમયના આલેખો]

નિષ્કર્ષઃ અત્રે, ફિરોઝ માટેનો અંતર – સમયનો આલેખ સાનિયા માટેના અંતર – સમયના આલેખની ઉપર છે, જે દર્શાવે છે કે ફિરોઝની ઝડપ સાનિયા કરતાં વધુ છે. આમ છતાં, બંનેની ઝડપ અનિયમિત છે.

પ્રવૃત્તિ 8.11 [પા.પુ. પાના નં 111].

→ દોરીનો એક ટુકડો લઈ તેના કોઈ એક છેડે પથ્થરનો નાનો ટુકડો બાંધો. દોરીના બીજા છેડાને પકડીને પથ્થરને અચળ ઝડપથી વર્તુળાકાર પથ પર ગતિ કરાવો, જે આકૃતિ 8.23માં દર્શાવેલ છે.

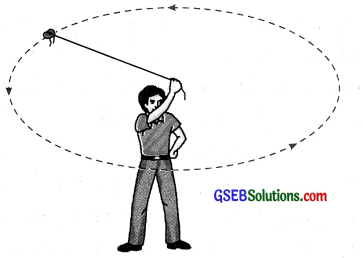
[આકૃતિ 8.23: વેગના અચળ મૂલ્ય સાથે વર્તુળાકાર પથ પર ગતિ કરતા પથ્થરનો ગતિપથ]

→ હવે દોરીને પથ્થર સહિત છોડી દો.

• શું તમે કહી શકો કે દોરી છોડ્યા બાદ પથ્થર કઈ દિશામાં ગતિ કરશે?
• આ પ્રવૃત્તિનું વારંવાર પુનરાવર્તન કરીને વર્તુળાકાર પથનાં જુદાં જુદાં બિંદુઓ પાસેથી પથ્થરને છોડો અને જુઓ કે પથ્થરની ગતિની દિશા સમાન છે કે નહિ.

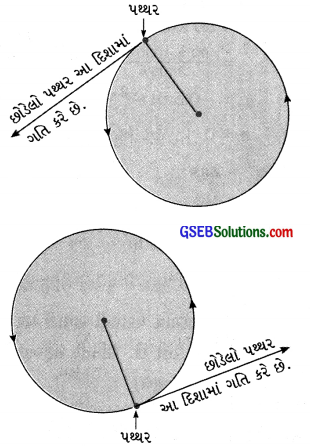
[આકૃતિ 8.24: પથ્થર વર્તુળ પથ પરના સ્પર્શકની દિશામાં ગતિ કરે છે.]

વર્તુળ પથ પરના જે બિંદુએથી જે ક્ષણે પથ્થરને મુક્ત કરવામાં આવે છે, પથ્થર વર્તુળના તે બિંદુએ દોરેલ સ્પર્શકની દિશામાં તે ક્ષણે છે ગતિ કરવા લાગે છે.

→ પથ્થરને વર્તુળ પથ પરનાં જુદાં જુદાં બિંદુએથી મુક્ત કરતાં, પથ્થર જુદી જુદી દિશામાં ગતિ કરવા લાગે છે; પણ ગતિની દિશા વર્તુળ – પથ પરના તે બિંદુએ દોરેલ સ્પર્શકની દિશામાં હોય છે.

→ અહીં પથ્થર વર્તુળ પથ પર ગતિ એટલા માટે કરે છે કે આપણે આપણા હાથ વડે તેના પર કેન્દ્રગામી બળ લગાડીએ છીએ.

જ્યારે દોરીના પકડેલા છેડાને મુક્ત કરવામાં આવે છે ત્યારે ? કેન્દ્રગામી બળ અદશ્ય થઈ જાય છે (શૂન્ય થાય છે) અને દિશાના જડત્વના ગુણધર્મને લીધે પથ્થર સુરેખ પથ પર ગતિ કરવા લાગે છે, એટલે કે પથ્થર વર્તુળ પથ પરના તે બિંદુએ દોરેલ સ્પર્શકની દિશામાં તે ક્ષણે ગતિ કરવા લાગે છે.

નિષ્કર્ષઃ પદાર્થને વર્તુળ પથ પર ગતિ કરતો રાખવા માટે તેના પર સતત કેન્દ્રગામી બળ લગાડતાં રહેવું પડે છે, જેના કારણે વર્તુળ પથ પરનાં જુદાં જુદાં બિંદુએ પદાર્થના વેગની માત્ર દિશા બદલાય છે અને પદાર્થ પ્રવેગી ગતિ કરી શકે છે.