GSEB Solutions Class 12 Maths Chapter 6 Application of Derivatives Ex 6.2

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 6 Application of Derivatives Ex 6.2 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 6 Application of Derivatives Ex 6.2

Question 1.
Show that the function given by f(x) = 3x + 17 is strictly increasing on R.
Solution:
f(x) = 3x + 17.
∴ f'(x) = 3 = + ve for all x ∈ R.
⇒ f is strictly increasing on R.

Question 2.
Show that the function given by f(x) = e^2x is strictly increasing on R.
Solution:
We have: f(x) = e^2x
⇒ f'(x) = 2^2x
Case I : When x > 0, then
f’ (x) = 2^2x
= 2[ 1 + (2x) + \(\frac{(2 x)^{2}}{2 !}+\frac{(2 x)^{3}}{3 !}+\ldots\) ]
∴ f'(x) > 0 for all x > 0.

Case II : When x = 0, then
f'(x) = 2e⁰ = 2
∴ f'(x) > 0 for x = 0.

Case III : When x < 0.
Let x = – y, where y is a positive quantity.
∴ f’ (x) = 2e^-2y = \(\frac{2}{e^{2 y}}\)
= \(\frac{2}{\text { Some +ve quantity }}\) > 0
⇒ f'(x) > 0 for x < 0.
Thus, f'(x) > 0 for all x ∈R.
Hence, e^2x is strictly increasing on R.

Question 3.
Show that the function given by f(x) = sin x is
(a) strictly increasing in (0, \(\frac{\pi}{2}\))
(b) strictly decreasing in (\(\frac{\pi}{2}\), 0)
(c) neither increasing nor decreasing in (0, π).
Solution:
We have: f(x) = sin x.
∴ f'(x) = cos x
(a) f'(x) = cos x is positive in the interval (0, \(\frac{\pi}{2}\))
⇒ f(x) is strictly increasing in (0, \(\frac{\pi}{2}\))

(b) f(x) cos x is negative in the interval (\(\frac{\pi}{2}\), π)
⇒ f(x) is strictly decreasing in (\(\frac{\pi}{2}\), π)

(c) f’ (x) – cos x is +ve in the interval (0, \(\frac{\pi}{2}\)),
while f'(x) is -ve in the interval (\(\frac{\pi}{2}\), π)
⇒ f’ (x) does not have the same sign in the interval (0, π)
Hence, f(x) is neither increasing nor decreasing in (0, π).

Question 4.
Find the intervals in which the function f given by, f(x) = 2x² – 3x is (a) strictly increasing, (b) strictly decreasing.
Solution:
f(x) = 2x² – 3x
∴ f'(x) = 4x – 3.
f'(x) = 0 at x = \(\frac{3}{4}\)
The point x = \(\frac{3}{4}\) divides the real line into two disjoint intervals

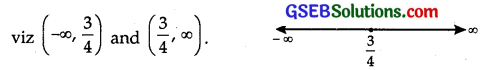
In the interval (-∞, \(\frac{3}{4}\)), f’ (x) is negative. Therefore, f is strictly decreasing in (-∞, \(\frac{3}{4}\))
In the interval (-∞, \(\frac{3}{4}\)), f’ is positive. Hence, f is strictly increasing in the interval (\(\frac{3}{4}\), ∞)

Question 5.
Find the intervals in which the function f given by f(x) = 2x³ – 3x² – 36x + 7 is (a)strictly increasing, (b) strictly decreasing.
Solution:
f(x) = 2x³ – 3x² – 36x + 7
∴ f (x) = 6x² – 6x – 36 = 6(x² – x – 6)
= 6(x -3)(x + 2)
⇒ f'(x) = 0 at x = 3 and x = – 2.
The points x = 3, x = -2 divide the real line into three disjoint intervals viz (-∞, – 2), (- 2, 3) and (3, ∞).

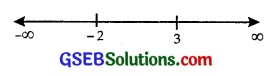
Now, f'(x) is +ve in the intervals (-∞, – 2) and (3, ∞), since in the interval (-∞, – 2), each factor x – 3, x + 2 is negative.
∴ f’ (x) = + ve
(a) f is strictly increasing in (-∞, – 2) u (3, ∞).
(b) In the interval (- 2, 3). x + 2 is +ve and x – 3 is -ve.
∴ f’ (x) = 6 (x – 3)(x + 2) = + x – = -ve.
∴ f is strictly decreasing in the interval (- 2, 3).

Question 6.
Find the intervals in which the following functions are strictly increasing or decreasing :
(a) x² + 2x – 5
(b) 10 – 6x – 2x²
(c) -2x² – 9x² – 12x + 1
(d) 6 – 9x – x²
(e) (x + 1)²(x – 3)³
Solution:
(a) We have : f(x) = x² + 2x – 5.
∴ f’ (x) = 2x + 2 = 2(x + 1)
The function/(x) will be increasing, if f ‘(x) > 0,
i.e., if 2(x + 1) > 0
⇒ x + 1 > 0.
⇒ x > – 1.
The function/(x) will be decreasing if f'(x) < 0,
i.e., 2(x + 1) < 0 ⇒ (x + 1) < 0.
⇒ x < -1.
Hence, f(x) is strictly increasing in (- 1, ∞) and strictly decreasing in (-∞, – 1).

(b) We have: f(x) = 10 – 6x – 2x².
∴ f'(x) = -6 – 4x = -2(3 + 2x)
Now, f(x) is increasing, if f'(x) > 0,
i. e., – 6 – 4x > 0.
i. e., – 4x > 6 ⇒ x < –\(\frac{3}{2}\)
and f'{x) is decreasing, if f'(x) < 0, i.e., if – 6 – 4x < 0,
i.e., – 4x < 6 ⇒ x > \(\frac{-3}{2}\)
Hence, f(x) is strictly increasing for x < \(\frac{-3}{2}\), i.e., in the interval (-∞, \(\frac{-3}{2}\)) and strictly decreasing for x > \(\frac{-3}{2}\) , i.e., in the interval (\(\frac{-3}{2}\), ∞)

(c) Let f(x) = – 2x³ – 9x² – 12x + 1.
∴ f'(x) = -6x² – 18x – 12
= – 6(x² + 3x + 2)
= – 6((x + 1)(x + 2).
f'(x) = 0 gives x = -1 or x = -2.
The points x = -2 and x = -1 (arranged in ascending order) divide the real line into three disjoint intervals namely, (- ∞, – 2), (- 2, -1) and (-1, ∞).
In the interval (-∞, – 2), i.e., -∞ < x < – 2,
(x + 1) and (x + 2) are negative.
∴ f'(x) = (-)(-)(-) = -ve.
⇒ f(x) is strictly decreasing in (-∞, – 2).
In the interval (- 2, – 1), i.e., – 2 < x < – 1,
(x + 1) is -ve and (x + 2) is positive.
∴ f'(x) = (-)(-)(+) = +ve.
⇒ f(x) is strictly increasing in (- 2, -1).
In the interval (- 1, ∞), i.e., – 1 < x < ∞,
(x + 1) and (x + 2) are both positive.
∴ f(‘x) = (-)(+)(+) = -ve.
⇒ f(x) is strictly decreasing in (- 1, ∞).
Hence, f(x) is strictly increasing for – 2 < x < -1 and strictly decreasing for x < -2 and x > – 1.

(d) We have: f(x) – 6 – 9x – x²
∴ f'(x) = – 9 – 2x
Now, f(x) is increasing, if f'(x) > 0, i.e., if – 9 – 2x > 0,
i.e., if -2x > 9 ⇒ x < \(\frac{-9}{2}\)
and f(x) is decreasing, if f{x) < 0, i.e., if – 9 – 2x < 0,
i.e., -2x < 9 ⇒ x > \(\frac{-9}{2}\).
Hence, f(x) is strictly increasing for x < \(\frac{-9}{2}\) and strictly decreasing for x > \(\frac{-9}{2}\).

(e) We have: f(x) = (x + 1)³ (x – 3)³
∴ f'(x) = 3(x + 1)² [\(\frac{d}{d x}\) (x + 1)] . (x – 3)³ + (x + 1)³ . 3(x – 3)² . \(\frac{d}{d x}\)(x – 3)
= 3(x + 1)² (x – 3)³ + 3(x + 1)3(x – 3)²
= 3(x + 1)²(x – 3)²(x – 3 + x + 1)
= 6(x + 1)²(x – 3)²(x – 1).
For f{x) to be increasing : .
f’ (x) > o.
⇒ 6(x + 1)² (x – 3)² (x – 1) > 0
⇒ (x – 1) > 0 [∵ 6(x + 1)²(x – 3)² > 0]
⇒ x > 1
But f ‘(x) = 0 at x = 3 .
⇒ f is strictly increasing in (1, 3) and (3, ∞)
So, f is strictly increasing in (1, 3) ∪ (3, ∞).
For f(x) to be decreasing :
f’ (x) < 0
⇒ 6(x + 1)² (x – 3)² (x – 1) < 0
⇒ (x – 1) < 0 [∵ 6(x + 1)²(x – 3)² > 0]
⇒ x < 1. But f ‘(x) = 0 at x = -1.
⇒ f is strictly decreasing in (-∞, – 1) and (-1, 1). So, f is strictly decreasing in (-∞, – 1) u (-1, 1).

Question 7.
Show that y = log (1 + x) – \(\frac{2 x}{2+x}\), x > -1 is an increasing function of x throughout its domain.
Solution:

Hence, y = log x – \(\frac{2 x}{2+x}\) is an increasing function of x for all values of x > – 1.

Note : From now onwards, we shall be using the terms increasing and decreasing for strictly increasing and strictly decreasing respectively, unless stated otherwise.

Question 8.
Find the values of x for which y = [x(x – 2)]² is an increasing function.
Solution:
Let y = [x(x – 2)]² = x²(x² – 4x + 4)
= x⁴ – 4x³ + 4x²
∴ \(\frac{d y}{d x}\) = 4x³ – 12x² + 8x.
For the function to be increasing :
\(\frac{d y}{d x}\) > 0
⇒ 4x³ – 12x² + 8x > 0
⇒ 4x(x² – 3x + 2) > 0
⇒ 4x(x – 1)(x – 2) > 0
Now, \(\frac{d y}{d x}\) = 0 gives x = 0 or x = 1 or x = 2.
These values divide the real line into three disjoint intervals, namely x < 0, 0 < x < 1 and x > 2.
∴ For 0 < x < 1, \(\frac{d y}{d x}\) = (+)(-)(-) = +ve
and for x > 2, \(\frac{d y}{d x}\) = (+)(+)(+) = +ve
Thus, the function is increasing for 0 < x < 1 and x > 2.
For x < 0, \(\frac{d y}{d x}\) = (-)(-)(-) = -ve so, the function is decreasing in x < 0.

Question 9.
Prove that y = \(\frac{4 \sin \theta}{(2+\cos \theta)}\) – θ is an increasing function of θ in [0, \(\frac{\pi}{2}\)]
Solution:
We have, y = \(\frac{4 \sin \theta}{(2+\cos \theta)}\) – θ

Question 10.
Prove that the logarthmic function is strictly increasing in (0, ∞).
Solution:
Let f(x) = log x.
So, we shall prove that f(x) is an increasing function for x > 0.
Now, f'(x) = \(\frac{1}{x}\)
Clearly, when x takes the values > 0, we observe that
∴ \(\frac{1}{2}\) > 0.
⇒ f’(x) > 0.
Hence, f(Y) is an increasing function for x > 0. .
i.e., f(x) is an increasing function whenever it is defined, i.e., on (0, ∞).

Question 11.
Prove that the function f given by f(x) = x² – x + 1 is neither strictly increasing nor strictly decreasing on (- 1, 1).
Solution:
f(x) = x² – x + 1
∴ f'(x) = 2x – 1 = 2(x – \(\frac{1}{2}\))
Now, – 1 < x < \(\frac{1}{2}\) ⇒ (x – \(\frac{1}{2}\))< 0.
⇒ 2(x – \(\frac{1}{2}\)) < 0 ⇒ f'(x)<0.
and, \(\frac{1}{2}\) < x < 1 ⇒ x – \(\frac{1}{2}\) > 0.
2(x – \(\frac{1}{2}\)) > 0 ⇒ f'(x) > 0.
Thus, f'(x) does not have the same sign throughout the interval (-1, 1).
Hence, f(x) is neither increasing nor decreasing in (-1, 1).

Question 12.
Which of the following functions are strictly decreasing on (0, \(\frac{\pi}{2}\))
(A) cos x
(B) cos 2x
(C) cos 3x
(D) tan x.
Solution:
(A) We have: f(x) = cos x f'(x) = – sin x
For 0 < x < \(\frac{\pi}{2}\), sin x > 0
∴ f’ (x) = – sin x < 0 in (0, \(\frac{\pi}{2}\))
∴ f'(x) is a decreasing function.

(B) We have : f(x) = cos 2x f'(x) = – 2 sin 2x
For 0 < x < \(\frac{\pi}{2}\)
or 0 < 2x < π, sin 2x is positive.
∴ f(x) is a decreasing function.

(C) We have : f(x) = cos 3x f'(x) = – 3 sin 3x
For 0 < x < \(\frac{\pi}{2}\) ⇒ 0 < 3x < \(\frac{3 \pi}{2}\).
Now, sin 3x is positive in 0 < 3x < π.
∴ f’ (x) < 0 ⇒ f(x) is decreasing.
And sin 3x is negative in π < 3x < \(\frac{3 \pi}{2}\).
∴ f'(x) > 0 ⇒ f(x) is increasing.
∴ f(x) is neither increasing nor decreasing in (0, \(\frac{\pi}{2}\)).
Hence, f(x) is not a decreasing function in (0, \(\frac{\pi}{2}\))

(D) We have: f(x) = tan x ‘
∴ f’ (x) = sec²x > 0 for all x ∈ (0, \(\frac{\pi}{2}\))
∴ f (x) is an increasing function.
Thus, (A) cos x and (B) cos 2x are strictly decreasing functions on (0, \(\frac{\pi}{2}\))

Question 13.
On which of the following intervals is the function f given by f(x) = x¹⁰⁰ + sin x – 1 strictly decreasing?
(A) (- 1, 1)
(B) (0, 1)
(C) (\(\frac{\pi}{2}\), π]
(D) (o, \(\frac{\pi}{2}\)).
Solution:
Let f(x) = x¹⁰⁰ + sinx – 1.
∴ f’ (x) = 100 x⁹⁹ + cos x
(A) For (- 1, 1), i.e., – 1 < x < 1, -1 < x⁹⁹ < 1
⇒ -100 < 100x⁹⁹ <100
Also, 0 < cosx < 1
⇒ f’ (x) can either be positive or negative on (- 1, 1).
∴ f(x) is neither increasing nor decreasing on (- 1, 1).

(B) For (0, 1), i.e., 0 < x < 1,
x⁹⁹ and cos x are both positive.
∴ f'(x)> 0.
⇒ f(x) is increasing on (0, 1).

(C) For (\(\frac{\pi}{2}\), π), i.e., \(\frac{\pi}{2}\) < x < π, x⁹⁹ & positive and – 1 < cos x < 0.
∴ f'(x) > 0.
⇒ f(x) is increasing on (\(\frac{\pi}{2}\), π)

(D) For (0, \(\frac{\pi}{2}\)), i.e., 0 < x < \(\frac{\pi}{2}\), x⁹⁹ and cos x are both positive.
∴ f’ (x) > 0.
⇒ f(x) is increasing on (0, \(\frac{\pi}{2}\)).
So, none of the above options gives the correct answer.

Question 14.
Find the least value of a such that the function f given by f(x) = x² + ax + 1 is strictly increasing on (1, 2).
Solution:
We have : f(x) = x² + ax + 1
∴ f’ (x) = 2x + a
Since f(x) is an increasing function on (1, 2), therefore
f’ (x) > 0 for all 1 < x < 2. Now, f “(x) = 2 for all x ∈ (1, 2) ⇒ f “(x) > 0 for all x ∈ (1, 2)
⇒ f’ (x) is an increasing function on (1, 2).
⇒ f’ (1) is the least value of f’ (x) on (1, 2).
But f’ (x) > 0 for all x ∈ (1, 2).Therefore,
f’ (1) > 0 ⇒ 2 + a > 0
⇒ a > – 2
Thus, the least value of a is – 2.

Question 15.
Let I be any interval disjoint from (-1, 1). Prove that the function f given by f(x) = x + \(\frac{1}{x}\) is strictly increasing on I.
Solution:

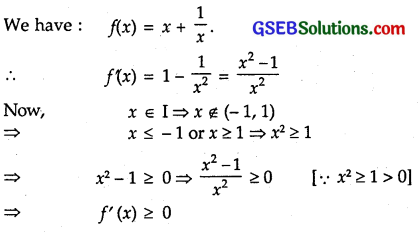
Thus, f'(x) > 0 for all x ∈ I.
Hence, f’ (x) is strictly increasing on I.

Question 16.
Prove that the function f given by f(x) = log sin x is strictly increasing on (o, \(\frac{\pi}{2}\)) and strictly decreasing on (\(\frac{\pi}{2}\), π).
Solution:
We have: f(x) = log sin x
∴ f’ (x) = \(\frac{1}{\sin x}\) . cos x = cot x.
When 0 < x < \(\frac{\pi}{2}\), f'(x) is +ve.
∴ f(x) is increasing.
When \(\frac{\pi}{2}\) < x < π, f'(x) is -ve.
∴ f(x) is decreasing.
Hence, f is strictly increasing on (0, \(\frac{\pi}{2}\)) and strictly decreasing on (\(\frac{\pi}{2}\), π)

Question 17.
Prove that the function f given by f(x) = log cos x is strictly decreasing on (0, \(\frac{\pi}{2}\)) and strictly increasing on (\(\frac{\pi}{2}\), π).
Solution:
f(x) = log cos x
∴ f’ (x) = \(\frac{1}{\cos x}\) (- sin x) = – tan x.
In the interval (0, \(\frac{\pi}{2}\)), f’ (x) is -ve.
∴ f is strictly decreasing in the interval.
In the interval (\(\frac{\pi}{2}\), π), f’ (x) is +ve.
[Since tan x is -ve in this interval]
∴ f is strictly increasing in the interval.

Question 18.
Prove that the function given by f(x) = x³ – 3x² + 3x -100 is increasing in R.
Solution:
f(x) = x³ – 3x² + 3x – 100
∴ f’ (x) = 3x² – 6x + 3 = 3(x² – 2x + 1)
= 3(x – 1)²
Now for x ∈ R, f'(x) = (x – 1)² ≥ 0
i. e., f’ (x) ≥ 0 for all x ∈ R.
Hence, f(a) is increasing in R.

Question 19.
The interval in which y = x² e^-x is increasing with respect to x is
(A) (-∞, ∞)
(B) (-2, 0)
(C) (2, ∞)
(D) (0, 2)
Solution:
f(x) = x²e^-x
∴ f’ (x) = 2x e^-x + x²(- e^-x)
= xe^-x(2 – x) = e^-x x(2 – x).
Now e^-x is positive for all x ∈ R
f’ (x) = 0 at x = 0, 2.
x = 0 and x = 2 divide the number line into three disjoint intervals viz (-∞, 0), (0, 2) and (2, ∞).

(a) Interval (-∞, 0)
x is -ve and 2 – x is +ve
∴ f'(x) = e^-x x(2 – x) = (+)(-)(+) = -ve.
⇒ f is decreasing in (-∞, 0).

(b) Interval (0, 2)
f’ (x) = e^-x x(2 – x) = (+)(+)(+) = +ve.
⇒ f is increasing in (0, 2).

(c) Interval (2, ∞)
f'(x) = e^-x x(2 – x) = (+)(+)(-) = -ve.
⇒ f is decreasing in the interval (2, ∞).
∴ Part (D) is the correct answer.