GSEB Solutions Class 11 Maths Chapter 13 Limits and Derivatives Ex 13.2

Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 13 Limits and Derivatives Ex 13.2 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 13 Limits and Derivatives Ex 13.2

Question 1.
Find the derivative of x² – 2 at x = 10.
Solution:
Derivative of f(x) at x = a is given by
f(a) = \(\lim _{h \rightarrow 0}\) \(\frac{f(a+h)-f(a)}{h}\)
Here, f(x) = x² – 2
a = 10, ∴ f(10 + h) = (10 + h)² – 2
and f(10) = 10² – 2.
∴ f(10 + h) – f(10) = [(10 + h)² – 2] – (10² – 2)
= (10 + h)² – 10² = (20 + h)h
∴ f(10) = \(\lim _{h \rightarrow 0}\) \(\frac{f(10+h)-f(10)}{h}\)
= \(\lim _{h \rightarrow 0}\) \(\frac{h(20+h)}{h}\).
= \(\lim _{h \rightarrow 0}\) (20 + h) = 20.

Question 2.
Find the derivative of 99x at x =100.
Solution:
Derivative of f(x) at x = 100 is
\(\lim _{h \rightarrow 0}\) = \(\frac{f(100+h)-f(100)}{h}\)
Now, f(x) = 99x.
∴ f(100 + h) = 99(100 + h).
and f(100) = 99 × 100.
∴ f(100 + h) – f(100) = 99(100 + h) – 99 × 100
= 99[100 + h – 100] = 99 × h
∴ f(100) = \(\lim _{h \rightarrow 0}\) \(\frac{99h}{h}\) = 99.

Question 3.
Find the derivative of x at x = 1.
Solution:
Derivative of f(x) = x at x = 1
f'(1) = \(\lim _{h \rightarrow 0}\) = \(\frac{f(x+h)-f(x)}{h}\).
= \(\lim _{h \rightarrow 0}\) \(\frac{(1+h)-1}{h}\)
= \(\lim _{h \rightarrow 0}\) \(\frac{h}{h}\) = 1.

Question 4.
Find the derivative of the following functions from first principles:
(i) x³ – 27
(ii) (x – 1)(x – 2)
(iii) \(\frac{1}{x^{2}}\)
(iv) \(\frac{x+1}{x-1}\)
Solution:
(i) f(x) = x³ – 27, Derivative f'(x) by first principle is given by

= 3x²

(ii) f(x) = (x – 1)(x – 2) = x² – 3x + 2

(iii) f(x) = \(\frac{1}{x^{2}}\).
Derivative of f(x) is given by

(iv) f(x) = \(\frac{x+1}{x-1}\).

Question 5.
For the function f(x) = \(\frac{x^{100}}{100}\) + \(\frac{x^{99}}{99}\) + …………… + \(\frac{x^{2}}{2}\) + x, prove that f ‘(1) = 100f ‘(0).
Solution:

Now, f ‘(1) = 1 + 1 + ………… to 100 terms = 100
Also, f ‘(0) = 1.
∴ f ‘(1) = 100 × 1 = 100 f ‘(0)
Hence, f ‘(1) = 100 f ‘(0).

Question 6.
Find the derivative of xⁿ + ax^n-1 + a²x^n-2 + …………. + a^n-1x + aⁿ for some fixed real number.
Solution:

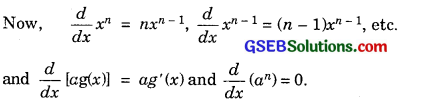
∴ f(x) = nx^n-1 + (n – 1)ax^n-2 + (n – 2)a²x^n-3 + …………. + a^n-1.

Question 7.
For some constants a and b, find the derivative of:
(i) (x – a)(x – b)
(ii) (ax² + b)²
(iii) \(\frac{x-a}{x-b}\)
Solution:
(i) f(x) = (x – a)(x – b)
We have:
f'(uv) = u’v + uv’.

∴ f'(x) = x – b + x – a = 2x – a – b.

(ii) f(x) = (ax² + b)² = a²x⁴ + 2abx² + b²
Now, \(\frac{d}{dx}\) x⁴ = 4x³ and \(\frac{d}{dx}\) x² = 2x and \(\frac{d}{dx}\) b² = 0.
∴ f(x) = a².4x³ + 2ab.2x + 0
= 4a²x³ + 4abx.

(iii)

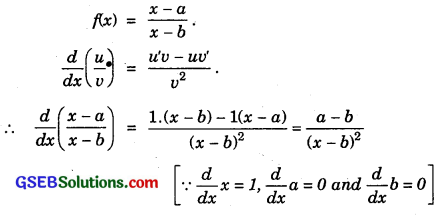
Question 8.
Find the derivative of \(\frac{x^{n}-a^{n}}{x-a}\) for some constant a.
Solution:

Question 9.
Find the derivative of
(i) 2x – \(\frac{3}{4}\)
(ii) (5x³ + 3x – 1)(x – 1)
(iii) x^-3(5 + 3x)
(iv) x⁵(3 – 6x^-9)
(v) x^-4(3 – 4x^-5)
(vi) \(\frac{2}{x+1}\) – \(\frac{x^{2}}{3 x-1}\)
Solution:
(i) Let f(x) = 2x – \(\frac{3}{4}\).
∴ f ‘(x) = 2.1 [∵ \(\frac{d}{dx}\) x = 1, \(\frac{d}{dx}\) (\(\frac{3}{4}\)) = 0]
= 2

(ii) Let f(x) = (5x³ + 3x – 1)(x – 1)
(uv)’ = u’v + uv’
∴ f(5x³ + 3x – 1)(x – 1)
= [\(\frac{d}{dx}\) (5x³ + 3x – 1)] (x – 1) + (5x³ + 3x – 1) \(\frac{d}{dx}\) (x – 1)
= (15x² + 3)(x – 1) + (5x³ + 3x – 1).1
= x(15x² + 3) – (15x² + 3) + (5x³ + 3x – 1)
= 20x³ – 15x² + 6x – 4.

(iii) Let f(x) = x^-3(5 + 3x) = 5x^-3 + 3x^-2
∴ f ‘(x) = 5(- 3) x^-4 + 3(- 2)x^-3

(iv) Let f(x) = x⁵(3 – 6x^-9) = 3x⁵ – 6x^-4
f ‘(x) = 3 × 5x⁴ – 6 × (- 4)x^-5
= 15x⁴ + 24x^-5

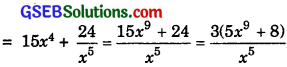
(v) Let f(x) = x^-4(3 – 4x^-5) = 3x^-4 – 4x^-9
f ‘(x) = 3.(- 4)x^-5 – 4. (- 9)x^-10

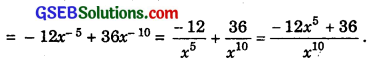
(vi) Let f(x) = \(\frac{2}{x+1}\) – \(\frac{x^{2}}{3 x-1}\)

Question 10.
Find the derivative of cos x from the first principle.
Solution:
f(x) = cos x.
∴ By first principle,

Question 11.
Find the derivative of the following functions:
(i) sin x cos x
(ii) sec x
(iii) 5secx + 4cos x
(iv) cosec x
(v) 3cot x + 5cosec x
(vi) 5sinx – 6cosx + 7
(vii) 2tanx – 7 secx
Solution:
(i) Let f(x) = sin x.cos x
So, f ‘(x) = u’v + uv’
= (\(\frac{d}{dx}\) sin x)cos x + sin x \(\frac{d}{dx}\)(cos x)
= cos x. cos x + sin x(- sin x)
= cos²x – sin²x = cos 2x.

(ii)

= sec x. tan x

Alternative method:

(vi) \(\frac{d}{dx}\) sin x = cos x and \(\frac{d}{dx}\) cos x = – sin x.
∴ \(\frac{d}{dx}\) (5sin x – 6cos x + 7) = 5cos x + 6sin x = 0
= 5cos x + 6sin x.

(vii) \(\frac{d}{dx}\) (sec x) = sec x tan x
and \(\frac{d}{dx}\)(tan x) = sec²x
∴ \(\frac{d}{dx}\)(2tan x – 7 secx) = 2sec²x – 2 sec x tan x
= sec x(2 sec x – 7 tan x).