GSEB Solutions Class 11 Maths Chapter 13 Limits and Derivatives Miscellaneous Exercise

Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 13 Limits and Derivatives Miscellaneous Exercise Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 13 Limits and Derivatives Miscellaneous Exercise

Question 1.
Find the derivatives of the following from first principle:
(i) – x
(ii) (- x)^-1
(iii) sin (x + 1)
(iv) cos ([x – \(\frac{π}{8}\))
Solution:
(i) Let f(x) = – x.

(ii)

(iii)

(iv)

Find the derivatives of the following functions, it is understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n integers.
2. ax + b
3. (px + q) (\(\frac{r}{x}\) + s)
4. (ax + b)(ex + d)²
5. \(\frac{ax+b}{cx+d}\)
6. \(\frac{1+\frac{1}{x}}{1-\frac{1}{x}}\)
7. \(\frac{1}{a x^{2}+b x+c}\)
8. \(\frac{ax+b}{p x^{2}+q x+r}\)
9. \(\frac{p x^{2}+q x+r}{a x+b}\)
10. \(\frac{a}{x^{4}}-\frac{b}{x^{2}}\) + cos x
11. 4\(\sqrt{x}\) + 2
12. (ax + b)ⁿ
13. (ax + b)ⁿ(cx + d)^m
14. sin (x + a)
15. cosec x cot x
16. \(\frac{cosx}{1+sinx}\)
17. \(\frac{sinx+cosx}{sinx-cosx}\)
18. \(\frac{sec x-1}{sec x+1}\)
19. sinⁿx
20. \(\frac{a+bsinx}{c+dcosx}\)
21. \(\frac{sin(x+a)}{cosx}\)
22. x⁴(5sinx – 3cosx)
23. (x² + 1) cos x
24. (ax² + sin x)(p + qcos x)
25. (x + cos x)(x – tan x)
26. \(\frac{4x+5sinx}{3x+7cosx}\)
27. \(\frac{x^{2} \cos \left(\frac{\pi}{4}\right)}{\sin x}\)
28. \(\frac{x}{1+tanx}\)
29. (x + secx)(x – tan x)
30. \(\frac{x}{\sin ^{n} x}\)
Solutions to questions 2 to 30:

2.

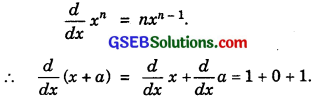
3. Let f(x) = (px + q) (\(\frac{r}{x}\) + s).
We have: (uv) = u’v + uv’

4. Let f(x) = (ax + b)(cx + d)²
To different (cx + d)², put cx + d = u.
So, (cx + d)² = u².

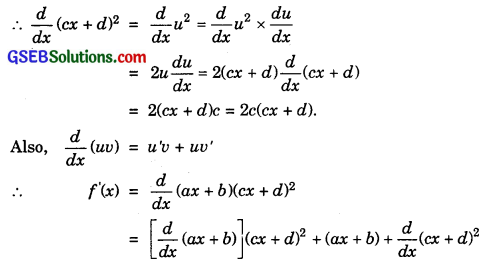
= a[(cx + d)² + (ax + b).2c(cx + d)
= 2c(ax + b)(cx + b) + a(cx + d)².

5. Let f(x) = \(\frac{ax+b}{cx+d}\)

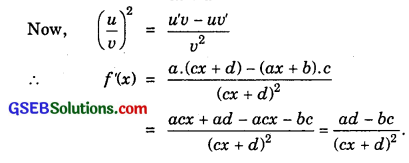
6.

7.

8.

9.

10.

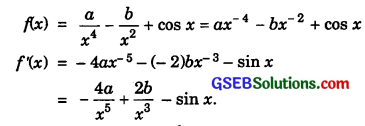
11. Let f(x) = 4\(\sqrt{x}\) + 2 = 4x^1/2 + 2.
∴ f ‘(x) = 4.\(\frac{1}{2}\)x^-1/2 + 0 = 2x^-1/2 = \(\frac{2}{\sqrt{x}}\)

12. Let f(x) = (ax + b)ⁿ. Put ax + b = u.
∴ f(x) = uⁿ

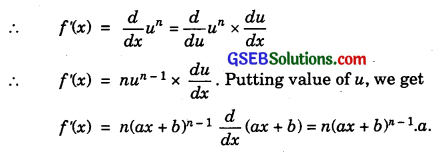
= na(ax + b)^n-1.

13. Let f(x) = (ax + b)ⁿ(cx + d)^m

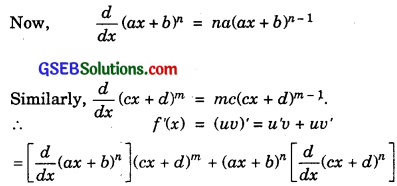
= na(ax + b)^n-1(cx + d)^m + (ax + b)ⁿ.mc(cx + d)^m-1
= (ax + b)^n-1(cx + d)^m-1 [na(cx + d) + mc(ax + b)].

14. Let f(x) = sin (x + a).
Putting x + a = u, we get \(\frac{du}{dx}\) = 1.
∴ f(x) = sin u.
∴ f ‘(x) = \(\frac{d}{dx}\) sin u = \(\frac{d}{du}\)sin u. \(\frac{du}{dx}\)
= cos u.\(\frac{du}{dx}\)
= cos (x + a).1
∴ f ‘(x) = cos (x + a).

15. Let f(x) = cosec x cot x
f ‘(x) = (uv)’ = u’v + uv’
= (\(\frac{d}{dx}\) cosec x) cot x + cosec x (\(\frac{d}{dx}\) cot x) ……………. (1)
Now \(\frac{d}{dx}\) cosec x = – cosec x cot x
\(\frac{d}{dx}\) cot x = – cosec²x
Putting these values in (1), we get
f ‘(x) = (- cosec x cot x) cot x + cosec x (- cosec² x)
= – cosec³x – cosec x cot² x.

16. Let f(x) = \(\frac{cosx}{1+sinx}\)

17. Let f(x) = \(\frac{sin x+cos x}{sin x-cos x}\)

18. Let f(x) = \(\frac{sec x-1}{sec x+1}\)

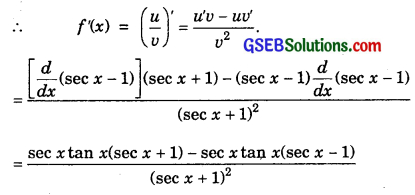
Note that \(\frac{d}{dx}\) sec x = sec x tan x.

19. Let f(x) = sinⁿx.

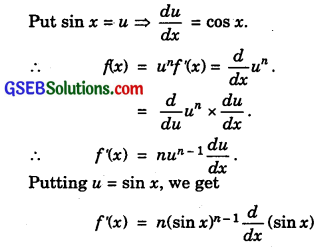
= nsin^n-1x cos x.

20. Let f(x) = \(\frac{a+bsinx}{c+dsinx}\)

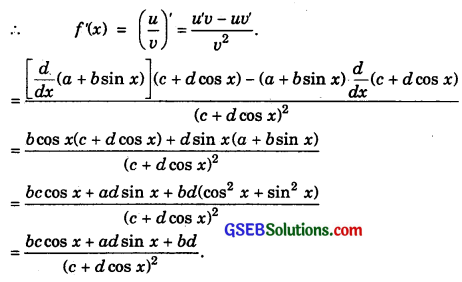
21. Let f(x) = \(\frac{sin(x + a)}{cosx}\)

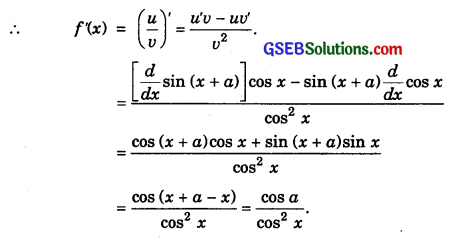
22. Let f(x) = x⁴(5sin x – 3cos x)
f ‘(x) = (uv)’ = u’v + uv’
= (\(\frac{d}{dx}\) x⁴) (5sin x – 3cos x) + x⁴\(\frac{d}{dx}\) (5sinx – 3cos x)
= 4x³(5sin x – 3cos x) + x⁴(5cos x + 3sin x)
= x³[5x cos x + 3xsin x + 20 sin x – 12cos x].

23. Let f(x) = (x² + 1)cos x.
f ‘(x) = (uv)’ = u’v + uv’
= [\(\frac{d}{dx}\) (x² + 1)]cos x + (x² + 1)\(\frac{d}{dx}\) (cos x)
= 2xcos x – (x² + 1) sin x.

24. Let f(x) = (ax² + sin x)(p + qcos x).
f ‘(x) = (uv)’ = u’v + uv’
= [\(\frac{d}{dx}\) (ax² + sin x)] (p + qcos x) + (ax² + sin x)\(\frac{d}{dx}\)(p + q cos x)
= (2ax + cos x)(p + q cos x) + (ax² + sin x)(- q sin x).
= – q sin x(ax² + sin x) + (p + q cos x)(2ax + cos x).

25. Let f(x) = (x + cos x)(x – tan x).
f ‘(x) = (uv)’ = u’v + uv’
= [\(\frac{d}{dx}\)(x + cos x)] (x – tan x) + (x + cos x)\(\frac{d}{dx}\)(x – tan x)
= (1 – sin x)(x – tan x) + (x + cos x)(1 – sec² x) [∵ \(\frac{d}{dx}\)tan x = sec² x]
= – (x + cos x)(sec² x – 1) + (x – tan x)(1 – sin x)
= – (x + cos x)tan² x + (x – tan x)(1 – sin x)

26.

27.

28.

29. Let f(x) = (x + sec x)(x – tan x)
f ‘(x) = (uv)’ = u’v + uv’
= [\(\frac{d}{dx}\)(x + sec x)] (x – tan x) + (x + sec x)\(\frac{d}{dx}\)(x – tan x)
= (1 + sec x tan x)(x – tan x) + (x + sec x)(1 – sec² x)
= (x + sec x)(1 – sec²x) + (x – tan x)(1 + sec x tan x)

30. Let f(x) = \(\frac{x}{\sin ^{n} x}\)
We have: \(\frac{d}{dx}\)x = 1 and \(\frac{d}{dx}\) sinⁿx = nsin^n-1cos x.