Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 7 Integrals Ex 7.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 7 Integrals Ex 7.1
Find an antiderivative (or integral) of the following by the method of inspection:
Question 1.
sin 2x
Solution:
We know that \(\frac{d}{dx}\) cos 2x = – 2sin 2x.
or \(\frac{d}{dx}\) (- \(\frac{1}{2}\) cos 2x) = sin 2x
∴ ∫sin 2x dx = – \(\frac{1}{2}\) cos 2x + C.
Question 2.
cos 3x
Solution:
2. We know that \(\frac{d}{dx}\) (sin 3x) = 3 cos 3x.
⇒ cos 3x = \(\frac{1}{3}\) \(\frac{d}{dx}\) (sin 3x)
⇒ cos 3x = \(\frac{d}{dx}\) (\(\frac{1}{3}\) sin 3x)
∴ An antiderivative of cos 3x is \(\frac{1}{3}\) sin 3x + C.
By using free Taylor Series Calculator, you can easily find the approximate value of the integration function
Question 3.
e2x
Solution:
We know that
\(\frac{d}{dx}\)(e2x) = 2e2x.
⇒ e2x = \(\frac{1}{2}\) \(\frac{d}{dx}\) (e2x)
⇒ e2x = \(\frac{d}{dx}\) (\(\frac{1}{2}\) e2x)
∴ An antiderivative of e2x is \(\frac{1}{2}\) e2x + C.
Question 4.
(ax + b)2
Solution:
We know that \(\frac{d}{dx}\) (ax + b)3 = 3a(ax + b)2.
⇒ (ax + b)2 = \(\frac{1}{3a}\) \(\frac{d}{dx}\)(ax + b)3
⇒ (ax + b)2 = \(\frac{d}{dx}\)[\(\frac{1}{3a}\)(ax + b)3]
∴ An antiderivative of (ax + b)2 = \(\frac{1}{3a}\)(ax + b)3 + C.
Question 5.
sin 2x – 4e3x
Solution:
We know that \(\frac{d}{dx}\)(cos 2x) = – 2 sin 2x.
⇒ sin 2x = \(\frac{d}{dx}\)(-\(\frac{1}{2}\) cos 2x)
and \(\frac{d}{dx}\)(4e3x) = 4 × 3e3x
⇒ 4e3x = \(\frac{d}{dx}\)(\(\frac{1}{3}\) e3x)
∴ An antiderivative of sin 2x – 4e3x is – \(\frac{1}{2}\) cos 2x – \(\frac{4}{3}\)e3x + C.
![]()
Find the following integrals:
Question
6. ∫(4e3x + 1)dx
Solution:
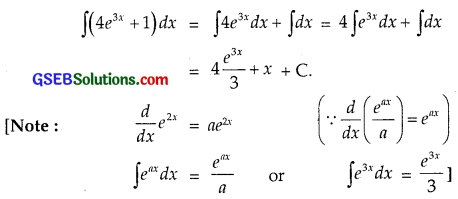
Question 7.
∫x2(1 – \(\frac{1}{x^{2}}\))dx
Solution:
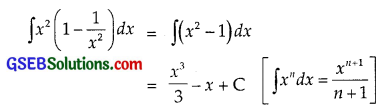
Question 8.
∫(ax2 + bx + c)dx
Solution:

Question 9.
∫(2x2 + ex) dx
Solution:
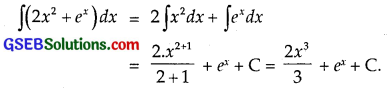
Question 10.
∫(\(\sqrt{x}\) – \(\frac{1}{\sqrt{x}}\))2 dx
Solution:
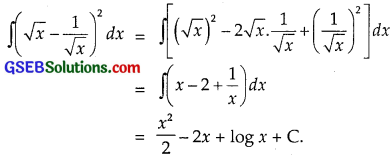
Question 11.
∫\(\frac{x^{3}+5 x^{2}-4}{x^{2}}\)dx
Solution:

Question 12.
∫\(\frac{x^{3}+3 x+4}{\sqrt{x}}\)dx
Solution:

Question 13.
∫\(\frac{x^{3}-x^{2}+x-1}{x-1}\)dx
Solution:
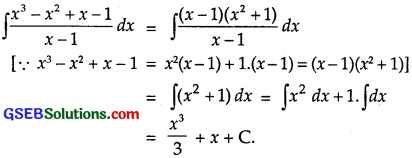
Question 14.
∫(1 – x)\(\sqrt{x}\) dx
Solution:
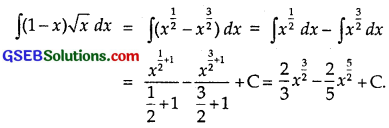
Question 15.
∫\(\sqrt{x}\)(3x2 + 2x + 3)dx
Solution:

Question 16.
∫(2x – 3cosx + ex)dx
Solution:
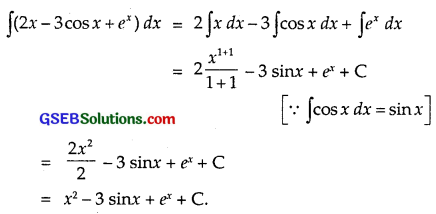
Question 17.
∫(2x2 – 3sinx + 5\(\sqrt{x}\))dx
Solution:
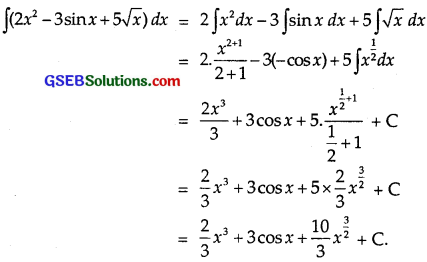
Question 18.
∫secx(sec x + tan x)dx
Solution:
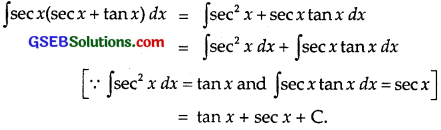
Question 19.
∫\(\frac{sec^{2}x}{cosec^{2}x}\)dx.
Solution:
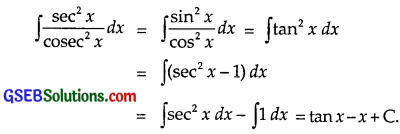
Question 20.
∫\(\frac{2-3 \sin x}{\cos ^{2} x}\) dx.
Solution:

![]()
Choose the correct answers in the following questions 21 and 22:
Question 21.
The antiderivative of (\(\sqrt{x}\) + \(\frac{1}{\sqrt{x}}\)) equals
(A) \(\frac{1}{3}\)x1/3 + 2x1/2 + C
(B) \(\frac{2}{3}\)x2/3 + \(\frac{1}{2}\)x2 + C
(C) \(\frac{2}{3}\)x3/2 + 2x1/2 + C
(D) \(\frac{3}{2}\)x3/2 + \(\frac{1}{2}\)x1/2 + C
Solution:

⇒ Part(C) is the correct answer.
Question 22.
If \(\frac{d}{dx}\) f(x) = 4x3 – \(\frac{3}{x^{4}}\) such that f(2) = 0, then f(x) is
(A) x4 + \(\frac{1}{x^{3}}\) – \(\frac{129}{8}\)
(B) x3 + \(\frac{1}{x^{4}}\) + \(\frac{129}{8}\)
(C) x4 + \(\frac{1}{x^{3}}\) + \(\frac{129}{8}\)
(D) x3 + \(\frac{1}{x^{4}}\) – \(\frac{129}{8}\)
Solution:

Putting C = – \(\frac{129}{8}\) in (1), we get
f(x) = x4 + \(\frac{1}{x^{3}}\) – \(\frac{129}{8}\)
⇒ Part(A) is the correct answer.