Gujarat Board GSEB Solutions Class 8 Maths Chapter 3 ચતુષ્કોણની સમજ Ex 3.2 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 3 ચતુષ્કોણની સમજ Ex 3.2
પ્રશ્ન 1.
નીચેની આકૃતિઓમાં x શોધોઃ
(a)
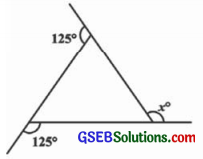
ઉત્તરઃ
આ આકૃતિ માટે આકૃતિના બધા બહિષ્કોણનાં માપનો સરવાળો = 360°
∴ x + 125° + 125° = 360°
∴ x + 250° = 360°
∴ x = 360° – 250° (∵ 250°ને જ.બા. લઈ જતાં)
∴ x = 110°
(b)
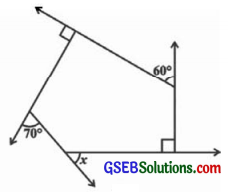
ઉત્તરઃ
આ આકૃતિમાં એક બહિષ્કોણ 90° છે અને બીજો અંત:કોણ 90° છે.
∴ આકૃતિમાં બે બહિષ્કોણ 90ના છે.
આ આકૃતિના બધા બહિષ્કોણનાં માપનો સરવાળો = 360°
∴ x + 90° + 60° + 90° + 70° = 360°
∴ x + 310° = 360°
∴ x = 360° – 310° (∵ 310ને જ.બા. લઈ જતાં)
∴ x = 50°
![]()
પ્રશ્ન 2.
નીચે પ્રમાણેની બાજુઓ ધરાવતા નિયમિત બહુકોણમાં બહિષ્કોણનું માપ શોધોઃ
(a) 9 બાજુ
ઉત્તરઃ
9 બાજુવાળા :
અહીં બહુકોણને 9 બાજુઓ છે. તેથી n = 9 લઈશું.
9 બાજુવાળા બહુકોણના બહિષ્કોણની સંખ્યા 9 હોય.
આ નિયમિત બહુકોણ છે. તેથી તેના દરેક બહિષ્કોણનું માપ સરખું હોય.
હવે, બહુકોણના બધા બહિષ્કોણનાં માપનો સરવાળો 360° થાય છે.
∴ 9 બાજુવાળા બહુકોણના દરેક બહિષ્કોણનું માપ
= \(\frac{360^{\circ}}{n}=\frac{360^{\circ}}{9}\) = 40°
(b) 15 બાજુ
ઉત્તરઃ
15 બાજુવાળા :
અહીં બહુકોણને 15 બાજુઓ છે. તેથી n = 15 લઈશું.
15 બાજુવાળા બહુકોણના બહિષ્કોણની સંખ્યા 15 હોય.
આ નિયમિત બહુકોણ છે. તેથી તેના દરેક બહિષ્કોણનું માપ સરખું હોય.
હવે, બહુકોણના બધા બહિષ્કોણનાં માપનો સરવાળો 360° થાય છે.
∴ 15 બાજુવાળા બહુકોણનાં દરેક બહિષ્કોણનું માપ
= \(\frac{360^{\circ}}{n}=\frac{360^{\circ}}{15}\) = 24°
પ્રશ્ન 3.
એક નિયમિત બહુકોણને કેટલી બાજુઓ હોય તો તેના દરેક બહિષ્કોણનું માપ 24° થાય?
ઉત્તરઃ
અહીં, બહુકોણ નિયમિત છે. તેથી તેના દરેક બહિષ્કોણનું માપ સરખું હોય.
બહુકોણના બધા બહિષ્કોણનાં માપનો સરવાળો 360° થાય છે.
હવે, આ બહુકોણના બહિષ્કોણનું માપ 24° છે.
∴ આ બહુકોણના ખૂણાઓની સંખ્યા = \(\frac{360^{\circ}}{24^{\circ}}\) = 15
આ નિયમિત બહુકોણને જેટલા ખૂણા તેટલી બાજુઓ હોય.
∴ આ બહુકોણને કુલ 15 બાજુઓ છે.
![]()
પ્રશ્ન 4.
એક નિયમિત બહુકોણને કેટલી બાજુઓ હોય તો તેના દરેક અંતઃકોણનું માપ 165° થાય?
ઉત્તરઃ
બહુકોણ નિયમિત છે અને તેના દરેક અંતઃકોણનું માપ 165° છે.
∴ બહુકોણના દરેક બહિષ્કોણનું માપ = 180° – 165° = 15
બહુકોણના બધા બહિષ્કોણનાં માપનો સરવાળો 360° થાય છે.
∴ બહુકોણની બાજુઓની સંખ્યા = \(\frac{360^{\circ}}{15^{\circ}}\) = 24
આ બહુકોણને કુલ 24 બાજુઓ છે.
પ્રશ્ન 5.
(a) એવો નિયમિત બહુકોણ શક્ય છે કે જેમાં દરેક બહિષ્કોણનું માપ 22° હોય?
ઉત્તરઃ
આ બહુકોણના બહિષ્કોણનું માપ 22° છે.
∴ બહુકોણની બાજુઓની સંખ્યા = \(\frac{360^{\circ}}{22^{\circ}}\) = \(\frac {180}{11}\)
જો આ બહુકોણ એ નિયમિત બહુકોણ હોય, તો તેની બાજુઓની સંખ્યા એ પૂર્ણ અંકમાં મળે.
જુઓ \(\frac{180^{\circ}}{11}\) એ પૂર્ણ સંખ્યા નથી.
∴ ના, નિયમિત બહુકોણ બહિષ્કોણનું માપ 22° ન હોઈ શકે.
(b) શું આ માપ નિયમિત બહુકોણના અંતઃકોણનું હોઈ શકે? કેમ?
ઉત્તરઃ
આ બહુકોણના અંદરના ખૂણાનું માપ 22° છે.
∴ બહુકોણના બહિષ્કોણનું માપ = 180° – 22° = 158° થાય.
∴ બહુકોણની બાજુઓની સંખ્યા = \(\frac{360^{\circ}}{158^{\circ}}=\frac{180}{79}\)
જો બહુકોણ એ નિયમિત બહુકોણ હોય, તો તેની બાજુઓની સંખ્યા એ પૂર્ણ અંકમાં મળે.
જુઓ \(\frac {180}{79}\) એ પૂર્ણ સંખ્યા નથી.
∴ ના, નિયમિત બહુકોણના અંતઃકોણનું માપ 22° ન હોઈ શકે.
![]()
પ્રશ્ન 6.
(a) નિયમિત બહુકોણમાં અંતઃકોણનું ઓછામાં ઓછું માપ કેટલું હોઈ શકે? કેમ?
ઉત્તરઃ
નિયમિત બહુકોણની બાજુઓની સંખ્યા ઓછામાં ઓછી 3 હોય.
∴ 3 બાજુઓવાળો નિયમિત બહુકોણ એ સમબાજુ ત્રિકોણ છે.
સમબાજુ ત્રિકોણના દરેક ખૂણાનું માપ 60° છે.
∴ નિયમિત બહુકોણના પ્રત્યેક અંતઃકોણનું માપ ઓછામાં ઓછું 60° હોઈ શકે.
(b) નિયમિત બહુકોણમાં બહિષ્કોણનું વધુમાં વધુ માપ કેટલું હોઈ શકે?
ઉત્તરઃ
નિયમિત બહુકોણના પ્રત્યેક અંતઃકોણનું માપ + તેના બહિષ્કોણનું માપ = 180°
હવે નિયમિત બહુકોણના પ્રત્યેક અંતઃકોણનું ઓછામાં ઓછું માપ = 60°
∴ બહુકોણના બહિષ્કોણનું માપ વધુમાં વધુ 180° – 60° = 120° હોય.