GSEB Solutions Class 9 Science Chapter 10 ગુરુત્વાકર્ષણ

Gujarat Board GSEB Solutions Class 9 Science Chapter 10 ગુરુત્વાકર્ષણ Textbook Questions and Answers, Intext Questions, Textbook Activites Pdf.

ગુરુત્વાકર્ષણ Class 9 GSEB Solutions Science Chapter 10

GSEB Class 9 Science ગુરુત્વાકર્ષણ Textbook Questions and Answers

સ્વાધ્યાયના પ્રશ્નોત્તર

પ્રશ્ન 1.
જો બે પદાર્થો વચ્ચેનું અંતર અડધું કરવામાં આવે, તો ? તેમની વચ્ચે લાગતું ગુરુત્વાકર્ષણ બળ કેટલું થશે?
ઉકેલ:
m₁ અને m₂ દળ ધરાવતા, તે અંતરે રહેલા બે પદાર્થો વચ્ચે લાગતું ગુરુત્વાકર્ષણ બળ,
F = G\(\frac{m_{1} m_{2}}{d^{2}}\) ……….. (1)
હવે જો d’ = \(\frac{d}{2}\) થાય, તો
F’ = G\(\frac{m_{1} m_{2}}{\left(d^{\prime}\right)^{2}}\) = G\(\frac{m_{1} m_{2}}{\left[\frac{d}{2}\right]^{2}}\) = \(\frac{4 \times G m_{1} m_{2}}{d^{2}}\) ………… (2)
સમીકરણ (1) અને (2) પરથી,
F’ = 4F એટલે કે ગુરુત્વાકર્ષણ બળનું મૂલ્ય 4 ગણું થાય.

પ્રશ્ન 2.
દરેક પદાર્થ પર લાગતું ગુરુત્વાકર્ષણ બળ તેમના દ્રવ્યમાનના સમપ્રમાણમાં હોય છે, તો પછી એક ભારે પદાર્થ હલકા પદાર્થની સાપેક્ષમાં વધારે ઝડપથી નીચે કેમ પડતો નથી?
ઉત્તરઃ
ન્યૂટનના ગુરુત્વાકર્ષણના સાર્વત્રિક નિયમ પરથી Me દળવાળી પૃથ્વી અને m દળવાળા પદાર્થ વચ્ચે લાગતું ગુરુત્વાકર્ષણ ખળ F = \(\frac{G M_{\mathrm{e}} m}{R_{\mathrm{e}}{ }^{2}}\)
જ્યાં, R_e = પૃથ્વીની ત્રિજ્યા
હવે, ન્યૂટનના ગતિના બીજા નિયમ પરથી,
F = mg
∴ mg = \(\frac{G M_{\mathrm{e}} m}{R_{\mathrm{e}}{ }^{2}}\)
∴ g = \(\frac{G M_{\mathrm{e}}}{R_{\mathrm{e}}^{2}}\) = અચળ
તેથી જુનું મૂલ્ય પદાર્થના દળ ‘m’ પર આધારિત નથી. આથી બધા જ પદાર્થો નીચે, પૃથ્વી તરફ એકસરખા પ્રવેગથી પડે છે.

પ્રશ્ન 3.
પૃથ્વી તથા તેની સપાટી પર રાખેલ 1kgના પદાર્થ વચ્ચે લાગતા ગુરુત્વીય બળનું મૂલ્ય કેટલું હશે? (પૃથ્વીનું દ્રવ્યમાન 6 × 10²⁴ kg તથા પૃથ્વીની ત્રિજ્યા 6.4 × 10 ⁶ m છે.) 1
ઉકેલ:
અત્રે, પદાર્થનું દળ m = 1 kg
પૃથ્વીનું દળ M_e = 6 × 10²⁴ kg
પૃથ્વીની ત્રિજ્યા R_e = 6.4 × 10⁶ m
પૃથ્વી તથા તેની સપાટી પર રાખેલ 1 kg દળના પદાર્થ વચ્ચે લાગતા ગુરુત્વીય બળનું મૂલ્ય,
F = \(\frac{G M_{\mathrm{e}} m}{R_{\mathrm{e}}^{2}}\)
= \(\frac{6.67 \times 10^{-11} \times 6 \times 10^{24} \times 1}{\left(6.4 \times 10^{6}\right)^{2}}\)
= \(\frac{6.67 \times 6 \times 10^{13}}{6.4 \times 6.4 \times 10^{12}}\)
= \(\frac{6.67 \times 6 \times 10}{6.4 \times 6.4}\)
= 9.77 N ≈ 9.8N

પ્રશ્ન 4.
પૃથ્વી તથા ચંદ્ર એકબીજાને ગુરુત્વીય બળથી આકર્ષે છે. શું પૃથ્વી જે બળથી ચંદ્રને આકર્ષે છે તે બળ, ચંદ્ર પૃથ્વીને આકર્ષે છે તે બળ કરતાં મોટું હોય છે, નાનું હોય છે કે સમાન હોય છે? સમજાવો કેમ?
ઉત્તરઃ
પૃથ્વી જેટલા બળથી ચંદ્રને પોતાની તરફ આકર્ષે છે તેટલા જ બળથી ચંદ્ર પણ પૃથ્વીને પોતાની તરફ આકર્ષે છે, કારણ કે ન્યૂટનના ગતિના ત્રીજા નિયમ અનુસાર ક્રિયા બળ અને પ્રતિક્રિયા બળ સમાન મૂલ્યના અને પરસ્પર વિરુદ્ધ દિશામાં હોય છે તથા જુદા જુદા પદાર્થો પર લાગે છે.
તેથી બંને એકબીજાને સમાન મૂલ્યના બળ વડે આકર્ષે છે, પણ બળની દિશા વિરુદ્ધ હોય છે.

પ્રશ્ન 5.
જો ચંદ્ર પૃથ્વીને આકર્ષિત કરતો હોય, તો પૃથ્વી ચંદ્ર તરફ ગતિ કેમ નથી કરતી?
ઉત્તરઃ
જેટલા બળ Fથી ચંદ્ર પૃથ્વીને આકર્ષે છે તેટલા જ બળ Fથી પૃથ્વી ચંદ્રને આકર્ષે છે.
પણ, પૃથ્વીનું દળ M_e ≈ (ચંદ્રનું દળ M_m)100
હવે, ન્યૂટનના ગતિના બીજા નિયમ પરથી,
બળ F = દળ m × પ્રવેગ a
∴ પ્રવેગ a = \(\frac{F}{m}\)
∴ a ∝ \(\frac{1}{m}\) (∵ F સમાન)
: પૃથ્વીમાં ઉભવતો પ્રવેગ નગણ્ય છે. તેથી પૃથ્વી ચંદ્ર તરફ ગતિ કરતી નથી.

પ્રશ્ન 6.
બે પદાર્થો વચ્ચે લાગતું ગુરુત્વાકર્ષણ બળ કેટલું થશે જો
(i) એક પદાર્થનું દ્રવ્યમાન બમણું કરવામાં આવે.
(ii) પદાર્થો વચ્ચેનું અંતર બમણું અને ત્રણ ગણું કરવામાં આવે.
(iii) બંને પદાર્થોનું દ્રવ્યમાન બમણું કરવામાં આવે.
ઉકેલ:
M અને m દળવાળા બે પદાર્થોનાં કેન્દ્રો વચ્ચેનું અંતર વે છે, તો તેમની વચ્ચે પ્રવર્તતું ગુરુત્વાકર્ષણ બળ,
F = \(\frac{G M m}{d^{2}}\)

(i) જો એક પદાર્થનું દળ બમણું કરવામાં આવે, તો
F’ = \(\frac{G(2 M) m}{d^{2}}\) = 2 × \(\frac{G M m}{d^{2}}\) = 2F
∴બળ બમણું થશે.

(ii) (a) બે પદાર્થો વચ્ચેનું અંતર બમણું કરવામાં આવે, તો
F’ = \(\frac{G M m}{(2 d)^{2}}\) = \(\frac{1}{4}\) × \(\frac{G M m}{d^{2}}\) = \(\frac{1}{4}\)F
∴ બળ ચોથા ભાગનું થશે.

(b) બે પદાર્થો વચ્ચેનું અંતર ત્રણ ગણું કરવામાં આવે, તો
F’ = \(\frac{G M m}{(3 d)^{2}}\) = \(\frac{1}{9}\) × \(\frac{G M m}{d^{2}}\) = \(\frac{1}{9}\)F
∴ બળ ચોથા ભાગનું થશે.

(iii) બંને પદાર્થોનું દળ બમણું કરવામાં આવે, તો
F’ = \(\frac{G(2 M)(2 m)}{d^{2}}\) = 4 × \(\frac{G M m}{d^{2}}\) = 4 F
∴ બળ ચાર ગણું થશે.

પ્રશ્ન 7.
ગુરુત્વાકર્ષણના સાર્વત્રિક નિયમનું શું મહત્ત્વ છે?
ઉત્તરઃ
ગુરુત્વાકર્ષણનો સાર્વત્રિક નિયમ ઘણી બધી ઘટનાઓને સમજાવવામાં અગત્યનો ભાગ ભજવે છે. જેમ કે …

• આપણને પૃથ્વી સાથે જકડી રાખતું બળ.
• પૃથ્વીની ફરતે થતું ચંદ્રનું કે બીજા કૃત્રિમ ઉપગ્રહોનું પરિક્રમણ.
• સૂર્યની ફરતે થતું ગ્રહોનું પરિક્રમણ .
• ચંદ્ર તથા સૂર્યને કારણે દરિયામાં આવતી ભરતી અને ઓટ.
• પૃથ્વીના વાતાવરણનું પૃથ્વી સાથે જકડાયેલું રહેવું તથા પૃથ્વી પર વરસાદ અને હિમવર્ષા થવી.

પ્રશ્ન 8.
મુક્ત પતનનો પ્રવેગ કેટલો છે?
ઉત્તર:
પદાર્થ પર લાગતાં પૃથ્વીના ગુરુત્વાકર્ષણ બળને લીધે પદાર્થ પૃથ્વી પર પડે છે. આ બળને લીધે પદાર્થમાં અચળ પ્રવેગ ઉદ્દભવે છે. આમ, જ્યારે પદાર્થ મુક્ત રીતે પૃથ્વી તરફ પડતો હોય ત્યારે તેમાં ઉદ્ભવતો પ્રવેગ એટલે મુક્ત પતનનો પ્રવેગ જે ગુરુત્વપ્રવેગ g જેટલો હોય છે.

પ્રશ્ન 9.
પૃથ્વી તથા કોઈ પદાર્થ વચ્ચે લાગતાં ગુરુત્વાકર્ષણ બળને આપણે શું કહીશું?
ઉત્તરઃ
પૃથ્વી તથા કોઈ પદાર્થ વચ્ચે લાગતાં ગુરુત્વાકર્ષણ બળને પદાર્થનું વજન “W’ કહે છે.

પ્રશ્ન 10.
અમિત પોતાના એક મિત્રના કહેવાથી ધ્રુવો પર કેટલાક ગ્રામ સોનું ખરીદે છે. તે સોનું વિષુવવૃત્ત પર પોતાના મિત્રને આપી દે છે. શું તેનો મિત્ર ખરીદાયેલા સોનાના વજનથી સંતુષ્ટ હશે? જો ના તો કેમ?
(સૂચન ધ્રુવો પર પુનું મૂલ્ય વિષુવવૃત્ત પરના મૂલ્ય કરતાં વધુ હોય છે.)
ઉત્તરઃ
અમિતનો મિત્ર ખરીદાયેલા સોનાના વજનથી સંતુષ્ટ – થશે નહીં.
કારણ કે, પૃથ્વીની સપાટી પર કોઈ પણ સ્થળે ગુરુત્વપ્રવેગ = g ∝\(\frac{1}{R_{\mathrm{e}}^{2}}\) જ્યાં, R_e = પૃથ્વીની ત્રિજ્યા : ધ્રુવ પ્રદેશ આગળ પૃથ્વીની ત્રિજ્યા, વિષુવવૃત્ત પાસેની ત્રિજ્યા – કરતાં લગભગ 21 km જેટલી) ઓછી છે. તેથી પૃથ્વીના ગુરુત્વપ્રવેગ – g નું મૂલ્ય ધ્રુવ પ્રદેશો પાસે વિષુવવૃત્ત કરતાં વધુ છે. : – ધ્રુવો પર સોનાનું વજન, વિષુવવૃત્ત પરના સોનાના વજન ના કરતાં વધુ હશે.

પ્રશ્ન 11.
એક કાગળની શીટ, તેના જેવી જ શીટને વાળીને બનાવેલ દડાની સાપેક્ષમાં ધીમેથી નીચે પડે છે. કેમ?
ઉત્તર:
કાગળની શીટનું ક્ષેત્રફળ, તેવી જ શીટ વડે બનાવેલ – દડાના ક્ષેત્રફળ કરતાં વધુ છે. તેથી અધોદિશામાંની ગતિ દરમિયાન કાગળની શીટ પર દડાની સાપેક્ષે હવાનું ઘર્ષણબળ વધુ લાગશે. તેથી દડાની સાપેક્ષે કાગળની શીટ ધીમેથી નીચે પડશે.

પ્રશ્ન 12.
ચંદ્રની સપાટી પર ગુરુત્વાકર્ષણ બળ, પૃથ્વીની સપાટી પરના – ગુરુત્વીય બળની સાપેક્ષમાં ગણું છે. એક 10 kgના પદાર્થનું ચંદ્ર – પર તથા પૃથ્વી પર ન્યૂટનમાં વજન કેટલું થશે?
ઉકેલ:
પદાર્થનું દળ m = 10 kg
પદાર્થનું પૃથ્વીની સપાટી પર વજન W_e = mg
= 10 × 9.8
= 98 N
હવે, ચંદ્ર પર પદાર્થનું વજન = \(\frac{1}{6}\) × (પદાર્થનું પૃથ્વી પર વજન)
= \(\frac{1}{6}\) × 98
= 16.33 N
આમ, આપેલ પદાર્થનું ચંદ્ર પર વજન ww = 16.33 N અને – પૃથ્વી પર વજન we = 98 N.

પ્રશ્ન 13.
એક દડાને ઊર્ધ્વદિશામાં 49 m s^-1ના વેગથી ફેંકવામાં – આવે છે, તો
(i) દડાએ પ્રાપ્ત કરેલ મહત્તમ ઊંચાઈ શોધો.
(ii) પૃથ્વીની સપાટી પર પાછા ફરવા માટે લાગતો કુલ સમય – શોધો.
ઉકેલ:
કાર્તેઝિયન સંજ્ઞા પ્રણાલી મુજબ ઊર્ધ્વદિશામાંના વેગને – ધન અને પૃથ્વીનો ગુરુત્વપ્રવેગ (જે અધોદિશામાં પૃથ્વીના કેન્દ્ર તરફ – છે તે) ઋણ લેવામાં આવે છે. અથવા ગતિની દિશાને ધન ગણતાં …
∴ અત્રે u = 49 m s^-1, a = – g = – 9.8m s^-2

(i) મહત્તમ ઊંચાઈએ દડાનો અંતિમ વેગ = 0
હવે, v² – u² = 2as
પણ, s = મહત્તમ ઊંચાઈ h અને v = 0
∴ 0 – (49)² = 2 (-9.8)
∴ h = \(\frac{49 \times 49}{2 \times 9.8}\) = 122.5 m

(ii) ધારો કે, દડાને મહત્તમ ઊંચાઈ પ્રાપ્ત કરવા માટે લાગતો સમય ‘t’ છે.
હવે, v = u + at
∴ 0 = 49 + (-9.8) 1 (∵ v = 0 અને a = – g = – 9.8 m s^-2).
∴ t = \(\frac{49}{9.8}\)
∴ t = 5 s
હવે,

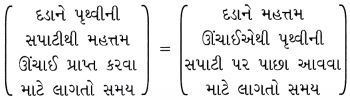
∴ પૃથ્વીની સપાટી પર પાછા ફરવા માટે દડાને લાગતો કુલ સમય = t + t
= 2 × t
= 2 × 5
= 10 s

પ્રશ્ન 14.
19.6 m ઊંચાઈના ટાવરની ટોચ પરથી એક પથ્થરને મુક્ત પતન કરવા દેવામાં આવે છે. પૃથ્વીની સપાટીને અડકે તે પહેલાં તેનો અંતિમ વેગ શોધો.
ઉકેલ:
અત્રે, u = 0
હવે, પથ્થર ટાવરની ટોચ પરથી મુક્ત પતન કરે છે. તેથી ગતિની દિશાને ધન ગણતાં a = + g = + 9.8 m s^-2 અને પથ્થર કાપેલું અંતર s = + 19.6 m
v² – u² = 2as
∴ v² – 0 = 2 9.8 × 19.6
∴ v² = 19.6 × 19.6
∴ v = +19.6 m s^-1
અહીં, પથ્થરની ગતિની દિશા(અધોદિશા)ને ધન ગણી છે.
∴ પથ્થર પૃથ્વીની સપાટીને અડકે તે પહેલાં તેનો અંતિમ વેગ
v = + 19.6 m s^-1

પ્રશ્ન 15.
એક પથ્થરને ઊર્ધ્વદિશામાં 40 m s^-1ના પ્રારંભિક વેગથી ફેંકવામાં આવે છે. g = 10 m s^-2 લઈને પથ્થર દ્વારા પ્રાપ્ત કરેલ મહત્તમ ઊંચાઈ શોધો. પથ્થર દ્વારા થયેલ કુલ સ્થાનાંતર તથા તેણે કાપેલ કુલ અંતર કેટલું? [3 ગુણ]
ઉકેલ:
અહીં, ગતિની દિશાને ધન ગણતાં,
u = + 40 m s^-1, a = – g = – 10 m s^-2
→ મહત્તમ ઊંચાઈએ પથ્થરનો અંતિમ વેગ = 0 હોય છે.
v² – u² = 2as
∴ 0 – (40)² = 2 (- 10) h (∵ s = મહત્તમ ઊંચાઈ h લેતાં)
∴ h = \(\frac{40 \times 40}{2 \times 10}\)
= 80 m
→ પથ્થરનું પ્રારંભિક સ્થાન અને ગતિ કર્યા બાદનું અંતિમ સ્થાન એક જ છે.
∴ સ્થાનાંતર = 0
→ પથ્થરે કાપેલું કુલ અંતર = 80 + 80
= 160 m

પ્રશ્ન 16.
પૃથ્વી તથા સૂર્ય વચ્ચે લાગતાં ગુરુત્વાકર્ષણ બળની ગણતરી કરો. પૃથ્વીનું દ્રવ્યમાન = 6 × 10²⁴ kg તથા સૂર્યનું દ્રવ્યમાન = 2 × 10³⁰ kg. બંને વચ્ચેનું સરેરાશ અંતર = 1.5 × 10¹¹ છે.
ઉકેલ:
પૃથ્વીનું દળ M_e = 6 × 10²⁴ kg
સૂર્યનું દળ M_s = 2 × 10³⁰ kg
બંને વચ્ચેનું સરેરાશ અંતર d = 1.5 × 10¹¹m
ગુરુત્વાકર્ષણ બળ F = \(\frac{G M_{\mathrm{e}} M_{s}}{d^{2}}\)
= \(\frac{6.67 \times 10^{-11} \times 6 \times 10^{24} \times 2 \times 10^{30}}{\left(1.5 \times 10^{11}\right)^{2}}\)
= \(\frac{6.67 \times 12 \times 10^{43}}{2.25 \times 10^{22}}\)
≈ 3.56 × 1022 N

પ્રશ્ન 17.
કોઈ પથ્થરને 100 m ઊંચા ટાવરની ટોચ પરથી પડતો મૂકવામાં આવે છે. તે જ સમયે બીજા પથ્થરને જમીન પરથી 25 m sના વેગથી ઊર્ધ્વદિશામાં ફેંકવામાં આવે છે, તો બંને પથ્થર ક્યારે અને ક્યાં એકબીજાને મળશે?
ઉકેલ:

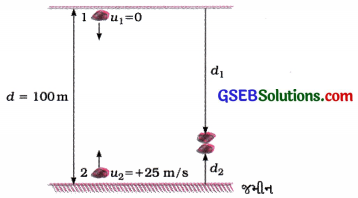
ધારો કે, બંને પથ્થર ગતિની શરૂઆત કર્યા બાદ t સમયે એકબીજાને મળે છે. તે વખતે પથ્થર 1 અધોદિશામાં d₁ જેટલું અને પથ્થર 2 ઊર્ધ્વદિશામાં d₂ જેટલું અંતર કાપે છે.
હવે, અધોદિશામાં ગતિ કરતા પથ્થર 1 માટે ગતિની દિશા ધન ગણતાં,
u₁ = 0
a₁ = + g₁ = +9.8m s^-2
∴ d₁ = u₁t + \(\frac{1}{2}\) a₁t²
= (0) t + \(\frac{1}{2}\) (9.8) t²
= 4.9 t²
ઊર્ધ્વદિશામાં ગતિ કરતા પથ્થર 2 માટે ગતિની દિશા ધન ગણતાં,
u₂ = + 25 m s¹
a₂ = – g₂ =- 9.8 m s^-2
∴ d₂ = u₂t + \(\frac{1}{2}\) a₂t²
= (+25) t + \(\frac{1}{2}\)(- 9.8) t²
= 25t – 4.9t²

→ જ્યારે બંને પથ્થર એકબીજાને મળશે ત્યારે d₁ + d₂ = d થાય.
∴ 4.9t² + 25 t – 4.9 t² = 100
∴ 25 t = 100
∴ t = 4 s
આમ, બંને પથ્થરોએ ગતિની શરૂઆત કર્યા બાદ 4s ને અંતે ૬ એકબીજાને મળશે.

→ જ્યારે બંને પથ્થર એકબીજાને મળશે ત્યારે
પથ્થર 1 વડે કપાયેલું અંતર,
d₁ = u₁t + \(\frac{1}{2}\) a₂t²
= (0) 4 + \(\frac{1}{2}\)(9.8) 4²
= (9.8) × 8
= 78.4 m
પથ્થર 2 વડે કપાયેલું અંતર,
d₂ = u₂t + \(\frac{1}{2}\) a₂t²
= (25) (4) + \(\frac{1}{2}\) (- 9.8) 4²
= 100 – (9.8) × 8
= 100 – 78.4
= 21.6 m
આમ, બંને પથ્થર એકબીજાને મળશે ત્યારે પથ્થર 1, ટાવરની ટોચ પરથી અધોદિશામાં 78.4 m અંતર અને પથ્થર 2, જમીનથી ઊર્ધ્વદિશામાં 21.6 m અંતર કાપેલ હશે.

પ્રશ્ન 18.
ઊર્ધ્વદિશામાં ફેંકવામાં આવેલ એક દડો ઉs બાદ ફેંકવાવાળાના હાથમાં પાછો આવે છે, તો
(a) તેને કેટલા વેગથી ફેંકવામાં આવેલ છે?
(b) દડાએ પ્રાપ્ત કરેલ મહત્તમ ઊંચાઈ કેટલી?
(c) 4s બાદ દડાનું સ્થાન શોધો.
ઉકેલ:
અહીં, દડાને શિરોલંબ ઊર્ધ્વદિશામાં ફેંકવામાં આવેલ છે. અને 6 s બાદ તે ફેંકનારના હાથમાં આવે છે. તેથી દડાના ઊર્ધ્વગમન માટેનો સમય = દડાનો અધોગમન માટેનો સમય = \(\frac{6}{2}\) = 3s

(a) દડાની ઊર્ધ્વગતિ માટે, ગતિની દિશાને ધન ગણતાં મહત્તમ
ઊંચાઈએ v = 0, t = 3s અને a = – g = – 9.8 m s^-2
v = u + at :
∴ 0 = u + (- 9.8) × 3
∴ u = + 29.4m s^-1

(b) s = ut + \(\frac{1}{2}\)at²
∴ h = 29.4 × 3 + \(\frac{1}{2}\) (- 9.8) × (3)² (∵ s = h = મહત્તમ ઊંચાઈ)
= 88.2 – 44.1 = 44.1 m

(c) દડાને ઊર્ધ્વદિશામાં ફેંક્યા બાદ 4 s ને અંતે દડાનું સ્થાન,
s = ut + \(\frac{1}{2}\)at²
= 29.4 × 4 + \(\frac{1}{2}\) × (- 9.8) × (4)
= 117.6 – 78.4 = 39.2 m
∴ દડો જમીનથી 39.2 mની ઊંચાઈએ હશે (અથવા મહત્તમ ઊંચાઈવાળા સ્થાનેથી નીચેની તરફ 44.1 – 39.2 = 4.9 m અંતરે દડો હશે.)

પ્રશ્ન 19.
કોઈ પ્રવાહીમાં ડુબાડેલ પદાર્થ પર ઉમ્બાવક બળ કઈ દિશામાં કાર્ય કરે છે?
ઉત્તર:
પ્રવાહીમાં ડુબાડેલ પદાર્થ પર લાગતું ઉગ્લાવક બળ શિરોલંબ ઊર્ધ્વદિશામાં હોય છે, એટલે કે પદાર્થના વજનની વિરુદ્ધ દિશામાં હોય છે.

પ્રશ્ન 20.
પાણીમાં ડુબાડેલ પ્લાસ્ટિકના બ્લોકને છોડી દેતાં તે પાણીની સપાટી પર કેમ આવી જાય છે?
ઉત્તર:
પ્લાસ્ટિકની ઘનતા પાણીની ઘનતા કરતાં ઓછી છે. તેથી પાણી વડે પ્લાસ્ટિકના બ્લૉક પર લાગતું ઉપ્લાવક બળ પ્લાસ્ટિકના વજન કરતાં વધુ છે. પરિણામે પ્લાસ્ટિકના બ્લૉકને પાણીની અંદરથી – છોડી દેતાં તે પાણીની સપાટી પર આવી જાય છે.

પ્રશ્ન 21.
50 g દળ ધરાવતા કોઈ પદાર્થનું કદ 20 cm છે. જો પાણીની ઘનતા 1 cmહોય, તો પદાર્થ તરશે કે ડૂબશે?
ઉકેલ:
અત્રે, પદાર્થનું દળ m = 50 g
પદાર્થનું કદ V = 20 cm
∴ પદાર્થની ઘનતા = = \(\frac{50 \mathrm{~g}}{20 \mathrm{~cm}^{3}}\) = 2.5 g m^-3
પાણીની ઘનતા = 1 g cm^-3 છે.
અહીં, પદાર્થની ઘનતા, પાણીની ઘનતા કરતાં વધુ છે. તેથી પદાર્થ પાણીમાં ડૂબશે.

પ્રશ્ન 22.
500 g ના સીલબંધ પૅકેટનું કદ 350 cm³ છે. પેકેટ 1 g cm^-3 ઘનતા ધરાવતા પાણીમાં ડૂબશે કે તરશે? આ પૅકેટ દ્વારા વિસ્થાપિત પાણીનું દળ કેટલું હશે?
ઉકેલ:
સીલબંધ પૅકેટનું દળ m = 500 g
સીલબંધ પૅકેટનું કદ V = 350 cm³
∴ પદાર્થની ઘનતા = = \(\frac{500}{350}\) = 1.428 g cm
પાણીની ઘનતા = 1 g cm^-3 હોય છે.
પૅકેટની ઘનતા, પાણીની ઘનતા કરતાં વધુ હોવાથી પૅકેટ પાણીમાં ડૂબી જશે.
અહીં, પૅકેટ પાણીમાં સંપૂર્ણ ડૂબે છે. તેથી પૅકેટ દ્વારા વિસ્થાપિત
પાણીનું દળ = (પેકેટનું કદ) × (પાણીની ઘનતા)
= (350 cm³) × (1 g cm^-3) = 350 g

GSEB Class 9 Science ગુરુત્વાકર્ષણ Intext Questions and Answers

Intext પ્રશ્નોત્તર [પા.પુ. પાના નં. 134]

પ્રશ્ન 1.
ગુરુત્વાકર્ષણનો સાર્વત્રિક નિયમ જણાવો.
ઉત્તરઃ
વિશ્વનો પ્રત્યેક પદાર્થ બીજા પદાર્થને પોતાની તરફ આકર્ષે છે. બે પદાર્થો વચ્ચેનું આ આકર્ષણ બળ તેમના દળના ગુણાકારના સમપ્રમાણમાં અને તેમની વચ્ચેના અંતરના વર્ગના વ્યસ્ત પ્રમાણમાં હોય છે. આ બળની દિશા બંને પદાર્થોને જોડતી રેખાની દિશામાં હોય છે.

પ્રશ્ન 2.
પૃથ્વી તથા તેની સપાટી પર રાખેલ કોઈ પદાર્થ વચ્ચે લાગતા ગુરુત્વાકર્ષણ બળનું મૂલ્ય શોધવા માટેનું સૂત્ર લખો.
ઉત્તર:
F = G\(\frac{M_{\mathrm{e} m}}{R_{\mathrm{e}}{ }^{2}}\)
જ્યાં, F = ગુરુત્વાકર્ષણ બળ
G = ગુરુત્વાકર્ષણનો સાર્વત્રિક અચળાંક
M_e = પૃથ્વીનું દળ
m = પદાર્થનું દળ
R_e = પૃથ્વીની ત્રિજ્યા

Intext પ્રશ્નોત્તર | પા.પુ. પાના નં. 136]

પ્રશ્ન 1.
મુક્ત પતનનું તમે શું અર્થઘટન કરશો?
ઉત્તર:
જ્યારે કોઈ પદાર્થને કોઈ પણ પ્રકારનું બાહ્ય બળ આપ્યા સિવાય અમુક ઊંચાઈએથી મુક્ત કરવામાં (છોડવામાં) આવે, ત્યારે તે પદાર્થ માત્ર પૃથ્વીના ગુરુત્વાકર્ષણ બળની અસર હેઠળ સુરેખ પથ : પર નીચે તરફ ગતિ કરે છે. આ સંજોગોમાં પદાર્થ મુક્ત પતન કરે છે તેમ કહેવાય.

પ્રશ્ન 2.
ગુરુત્વીય પ્રવેગનું તમે શું અર્થઘટન કરશો?
ઉત્તર:
પદાર્થ પર લાગતા પૃથ્વીના ગુરુત્વાકર્ષણ બળને લીધે તેમાં ઉદ્ભવતા પ્રવેગને ગુરુત્વીય પ્રવેગ કહે છે.

Intext પ્રશ્નોત્તર [પા.પુ. પાના નં. 138]

પ્રશ્ન 1.
પદાર્થના દળ તથા તેના વજન વચ્ચે શું તફાવત છે?
ઉત્તર:

દળ	વજન
1. પદાર્થમાં રહેલા દ્રવ્યના જથ્થાને પદાર્થનું દળ કહે છે.	1. પદાર્થ પર લાગતા ગુરુત્વાકર્ષણ બળને પદાર્થનું વજન કહે છે.
2. દળ અદિશ રાશિ છે.	2. વજન સદિશ રાશિ છે.
3. દળનો SI એકમ kg છે.	3. વજન એ એક પ્રકારનું બળ હોઈ, તેનો SI એકમ newton છે.
4. પદાર્થનું દળ ભૌતિક તુલા કે ત્રાજવા વડે મપાય છે.	4. પદાર્થનું વજન સ્પ્રિંગ કાંટા વડે મપાય છે.
5. પદાર્થનું દળ દરેક સ્થળે અચળ રહે છે.	5. પદાર્થનું વજન દરેક સ્થળે અચળ રહેતું નથી. તેનું મૂલ્ય જે- તે સ્થળના g પર આધારિત હોઈ બદલાય છે.

પ્રશ્ન 2.
કોઈ પદાર્થનું ચંદ્ર પર વજન પૃથ્વી પરના વજન કરતાં ગણું કેમ હોય છે?
ઉત્તર:
વ્યાપક રૂપે m દળના પદાર્થનું વજન W = mg
જ્યાં, g = ગુરુત્વપ્રવેગ = \(\frac{G M}{R^{2}}\) (જ્યાં, M =દળ, R =ત્રિજ્યા)
∴ m દળવાળા પદાર્થનું પૃથ્વી પર વજન,
W_e = mg_e – \(\frac{G M_{\mathrm{e}}}{R_{\mathrm{e}}^{2}}\) …………. (1)
તે જ પદાર્થનું ચંદ્ર પર વજન,
W_m = mg_m = \(\frac{G M_{\mathrm{m}}}{R_{\mathrm{m}}^{2}}\) ………….. (2)
સમીકરણ (2) અને (1) નો ગુણોત્તર લેતાં,
\(\frac{W_{\mathrm{m}}}{W_{\mathrm{e}}}\) = \(\frac{M_{\mathrm{m}}}{M_{\mathrm{e}}} \times\left(\frac{R_{\mathrm{e}}}{R_{\mathrm{m}}}\right)^{2}\)
હવે, પૃથ્વીનું દળ ચંદ્રના દળ કરતાં 100 ગણું છે.
∴ M_e = 100 M_m
અને પૃથ્વીની ત્રિજ્યા ચંદ્રની ત્રિજ્યા કરતાં 4 ગણી છે.
∴ R_e = 4 R_m
∴ \(\frac{W_{\mathrm{m}}}{W_{\mathrm{e}}}\) = \(\left(\frac{1}{100}\right) \times\left[\frac{4}{1}\right]^{2}\) = \(\frac{16}{100}\) ≈ \(\frac{1}{6}\)
આમ, આપેલ પદાર્થનું ચંદ્ર પર વજન પૃથ્વી પરના વજન કરતાં \(\frac{1}{6}\) ગણું છે.

Intext પ્રજ્ઞોત્તર [પા.પુ. પાના નં. 141]

પ્રશ્ન 1.
એક પાતળી અને મજબૂત દોરીથી બનેલા પટ્ટાની મદદથી સ્કૂલબૅગને ઉપાડવાનું મુશ્કેલ હોય છે. કેમ?
અથવા
કારણ આપોઃ સ્કૂલબૅગના પટ્ટા પહોળા રાખવામાં આવે છે.
ઉત્તર:
જ્યારે સ્કૂલબૅગને હાથ વડે અથવા ખભા વડે ઊંચકવામાં આવે છે ત્યારે હાથ પર કે ખભા પર લાગતું બળ સ્કૂલબૅગના વજન જેટલું હોય છે.

બૅગના પટ્ટા પહોળા રાખવાથી બૅગનું સમગ્ર વજન વિદ્યાર્થીના હાથ પરના અથવા ખભા પરના પહોળા પટ્ટા પર આવે છે. પરિણામે ક્ષેત્રફળ ન વધારે હોવાને લીધે દબાણ P = પરથી વિદ્યાર્થીના હાથ પર કે ખભા પર ઓછું દબાણ પ્રવર્તે છે, જેના કારણે વિદ્યાર્થી સરળતાથી સ્કૂલબૅગ ઊંચકી શકે છે.

પ્રશ્ન 2.
ઉપ્લાવકતાનું તમે શું અર્થઘટન કરશો?
ઉત્તર:
જ્યારે કોઈ પદાર્થને આપેલ પ્રવાહીમાં અંશતઃ કે સંપૂર્ણપણે ડુબાડવામાં આવે છે ત્યારે પ્રવાહી દ્વારા પદાર્થ પર ઊર્ધ્વદિશામાં બળ લાગે છે, જેને ઉપ્લાવક બળ કહે છે. પ્રવાહીના જે ગુણધર્મને લીધે ઉલ્લાવક બળ લાગે છે, તેને ઉલ્લાવકતા (Buoyancy) કહે છે.

પ્રશ્ન 3.
પાણીની સપાટી પર કોઈ પદાર્થને રાખતાં તે કેમ તરે છે અથવા ડૂબે છે?
ઉત્તર:
પદાર્થની ઘનતા અને પાણીની ઘનતાનાં મૂલ્યો વડે નક્કી થઈ શકે કે આપેલ પદાર્થ પાણીમાં તરશે કે ડૂબશે.

• જો પદાર્થની ઘનતા, પાણીની ઘનતા કરતાં ઓછી હોય, તો તે પદાર્થ પાણીમાં તરે છે.
• જો પદાર્થની ઘનતા, પાણીની ઘનતા કરતાં વધુ હોય, તો તે પદાર્થ પાણીમાં ડૂબે છે.

Intext પ્રશ્નોત્તર [પા.પુ. પાના નં 142]

પ્રશ્ન 1.
એક વજનકાંટા પર તમારું વજન 42 N નોંધાય છે. શું તમારું દળ 42 N કરતાં વધારે છે કે ઓછું?
ઉત્તર:
42 N કરતાં વધું, કારણ કે વજનકાંટો એ એક પ્રકારનું સ્વિંગ બૅલેન્સ છે, જે વસ્તુનું વજન માપે છે દળ નહિ.
જ્યારે આપણે વજનકાંટા પર ઊભા રહીએ છીએ ત્યારે આપણું વજન (એટલે કે આપણા પર લાગતું પૃથ્વીનું ગુરુત્વાકર્ષણ બળ) શિરોલંબ અધોદિશામાં હોય છે પણ હવા દ્વારા આપણા શરીર પર લાગતું ઉલ્લાવક બળ શિરોલંબ ઊર્ધ્વદિશામાં હોય છે.

તેથી આપણે દેખીતું વજન (= સાચું વજન – ઉપ્લાવક બળ), સાચા વજન કરતાં ઓછું હોય છે. વજનકાંટો દેખીતું વજન માપે છે. તેથી આપણું સાચું વજન 42 N કરતાં વધુ હશે.

પ્રશ્ન 2.
તમારી પાસે રૂ ભરેલો કોથળો અને લોખંડનો સળિયો છે. તેમને વજનકાંટા પર મૂકતાં બંનેનું દળ 100 kg નોંધાય છે. વાસ્તવમાં એક પદાર્થ બીજા કરતાં ભારે છે. શું તમે કહી શકશો કે કયો પદાર્થ ભાવે છે અને કેમ?
ઉત્તર:
રૂ(Cotton)ની ઘનતા લોખંડની ઘનતા કરતાં ઓછી છે, જેના લીધે 100 kg દળવાળા રૂનું કદ 100 kg દળવાળા લોખંડ કરતાં વધુ હશે.

વધુ કદના કારણે 100 kg દળવાળું રૂ, 100 kg દળવાળા રે લોખંડ કરતાં વધારે હવાનું વિસ્થાપન (સ્થાનાંતરણ) કરશે. તેથી રૂ પર છે હવા દ્વારા લાગતું ઉલ્લાવક બળ, લોખંડ કરતાં વધુ હશે. પરિણામે વજનકાંટો જે ખરેખર દેખીતું વજન (= સાચું વજન – ઉલ્લાવક બળ) માપે છે, તે લોખંડ કરતાં રૂનું વજન વધુ દર્શાવે છે.
હવે,
વસ્તુનું સાચું વજન = (વસ્તુનું દેખીતું વજન) + (ઉલ્લાવક બળ)
∴ હવામાં 100 kg દળવાળા રૂનું સાચું વજન, હવામાં માપેલા લોખંડ કરતાં વધુ હશે.

GSEB Class 9 Science ગુરુત્વાકર્ષણ Textbook Activities

પ્રવૃત્તિ 10.1 [પા.પુ. પાના નં 131]

• દોરીનો એક ટુકડો લો.
• તેના એક છેડા પર એક નાનો પથ્થર બાંધો. દોરીના બીજા છેડાને પકડીને પથ્થરને વર્તુળાકાર માર્ગે આકૃતિ 10.1માં દર્શાવ્યા પ્રમાણે ઘુમાવો.
• પથ્થરની ગતિની દિશા જુઓ.
• હવે દોરીને છોડી દો.
• ફરીથી પથ્થરની ગતિની દિશા જુઓ.

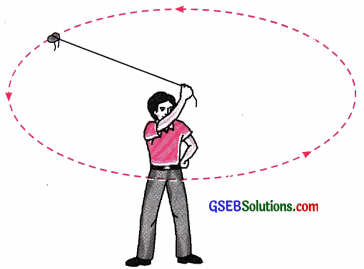
[આકૃતિ 10.1: પથ્થર દ્વારા અચળ ઝડપે વર્તુળાકાર પથ પર થતી ગતિ]

ચર્ચા-વિચારણા: પથ્થર વર્તુળાકાર પથ પર ગતિ કરે છે તેનું કારણ તેના પર લાગતું કેન્દ્રગામી (કેન્દ્ર તરફ લાગતું) બળ છે, જે આપણા હાથ વડે દોરી મારફતે પથ્થર પર લાગે છે. જ્યાં સુધી પથ્થર પર આ કેન્દ્રગામી બળ આપણા હાથ વડે લાગતું રહે છે ત્યાં સુધી પથ્થર વર્તુળમાર્ગે ગતિ કરતો રહે છે.

જ્યારે દોરીને છોડી દેવામાં આવે છે ત્યારે કેન્દ્રગામી બળ શૂન્ય થઈ જાય છે. પરિણામે પથ્થર (દિશાના) જડત્વના ગુણધર્મને લીધે વર્તુળપથ પરના તે બિંદુ આગળના સ્પર્શકની દિશામાં ફંટાઈ જાય છે – સુરેખ ગતિ કરવા માંડે છે.

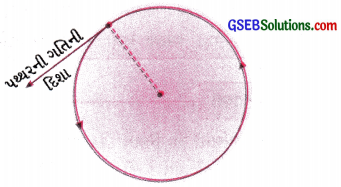
[આકૃતિ 10.2: દોરીને છોડી દેતાં થતી પથ્થરની ગતિ
દોરીને પથ્થરની ગતિ દરમિયાન કોઈ પણ ક્ષણે છોડી દેતાં, પથ્થર વર્તુળપથ પરના તે બિંદુ પાસેના સ્પર્શકની દિશામાં સુરેખ માર્ગે ગતિ કરવા લાગે છે.

નિષ્કર્ષ: દરેક ક્ષણે પથ્થરની ગતિની દિશા તેના પર લાગતાં કેન્દ્રગામી બળને લીધે બદલાયા કરે છે. જ્યારે કેન્દ્રગામી બળ શૂન્ય બને છે ત્યારે દિશાના જડત્વના ગુણધર્મને લીધે પથ્થર વર્તુળપથ પરના તે બિંદુ પાસેના સ્પર્શકની દિશામાં સુરેખ પથ પર ગતિ કરવા લાગે છે.

પ્રવૃત્તિ 10.2 [પા.પુ. પાના નં 134]

• એક પથ્થર લો.
• તેને ઉપર તરફ ફેંકો.
• તે એક નિશ્ચિત ઊંચાઈ સુધી પહોંચે છે પછી તે નીચે પડવા લાગે છે. વિચાર કરો.

ચર્ચા-વિચારણા જ્યારે પથ્થરને જમીન પરથી શિરોલંબ ઊર્ધ્વદિશામાં ફેંકવામાં આવે છે ત્યારે તેના પર સતત પૃથ્વીનું અચળ ગુરુત્વાકર્ષણ બળ (F = mg) અધોદિશામાં લાગે છે. જેના કારણે પદાર્થની ઊર્ધ્વગતિ નિયમિત પ્રતિપ્રવેગી બને છે. પરિણામે પદાર્થનો વેગ 9.8 m/sના દરે સતત ઘટતો જાય છે.

અમુક નિશ્ચિત ઊંચાઈએ તેનો વેગ શૂન્ય થાય છે. હવે પદાર્થ વધુ ઉપર તરફ જઈ શકતો નથી, જેને પદાર્થો પ્રાપ્ત કરેલી મહત્તમ ઊંચાઈ કહે છે. અત્રે પદાર્થ ક્ષણ પૂરતો સ્થિર રહે છે.

પૃથ્વીનું ગુરુત્વાકર્ષણ બળ પદાર્થને પોતાની તરફ ખેંચે છે. જો તે પદાર્થ માત્ર ગુરુત્વાકર્ષણ બળને લીધે પૃથ્વી તરફ અધોદિશામાં ગતિ કરે તો તેને પદાર્થનું મુક્ત પતન કહે છે. આ મુક્ત પતન દરમિયાન પદાર્થ પૃથ્વી તરફ પ્રવેગી ગતિ કરે છે. આ પ્રવેગી ગતિ પદાર્થ પર લાગતા ગુરુત્વાકર્ષણ બળને લીધે છે. તેથી આ પ્રવેગને ગુરુત્વાકર્ષણને કારણે ઉદ્ભવતો પ્રવેગ (ગુરુત્વીય પ્રવેગ) કહે છે. તેને 9 વડે દર્શાવાય છે અને તેનું મૂલ્ય 9.8 m s^-2 છે.

નિષ્કર્ષ: પૃથ્વીનું ગુરુત્વાકર્ષણ બળ પદાર્થની ઊર્ધ્વગતિ અને મુક્ત પતનમાં અગત્યનો પાયાનો ભાગ ભજવે છે.

પ્રવૃત્તિ 10.૩ [પા.પુ. પાના નં 135]

કાગળની એક શીટ તથા એક પથ્થર લો. બંનેને એકસાથે કોઈ ઇમારતના પ્રથમ માળેથી એકસાથે પડતાં મૂકો. જુઓ કે તે બંને એકસાથે જમીન પર પહોંચે છે કે નહિ. પછી વિચારો.

ચર્ચા-વિચારણા: જ્યારે કાગળની એક શીટ અને પથ્થરને ઇમારતના પ્રથમ માળેથી એકસાથે પડતાં મૂકવામાં આવે છે ત્યારે તેઓ એકસાથે જમીન પર પહોંચતા નથી. કાગળની શીટ પથ્થર કરતાં સહેજ મોડે જમીન પર પહોંચે છે. કારણ કે કાગળની શીટ અને પથ્થર બંને પર હવાનું અવરોધક બળ એકસરખું લાગતું નથી. કાગળની શીટનું ક્ષેત્રફળ વધુ હોવાથી તેના પર પથ્થર કરતાં વધુ અવરોધક બળ લાગે છે.

પરંતુ જો શૂન્યાવકાશિત કરેલા (હવા વગરના) કાચના વાસણમાં ઉપરોક્ત પ્રવૃત્તિ કરવામાં આવે, તો કાગળની શીટ અને પથ્થર પર કોઈ અવરોધક બળ લાગતું ન હોવાના કારણે બંને એકસાથે વાસણના તળિયે પહોંચે છે.

નિષ્કર્ષ: પૃથ્વીના ગુરુત્વાકર્ષણ બળને લીધે પદાર્થમાં ઉદ્ભવતો પ્રવેગ એટલે કે ગુરુત્વપ્રવેગ જે પદાર્થના દળ પર આધારિત નથી. ગુરુત્વપ્રવેગ gનું મૂલ્ય કોઈ પણ દળ ધરાવતા પદાર્થ માટે સમાન હોય છે.

પ્રવૃત્તિ 10.4 [પા.પુ. પાના નં. 140]

• પ્લાસ્ટિકની એક ખાલી બૉટલ લો. બૉટલના મુખને હવાચુસ્ત ઢાંકણથી બંધ કરી દો. તેને એક પાણી ભરેલ ડોલમાં મૂકો. તમે જોશો કે બૉટલ તરે છે.
• બૉટલને પાણીમાં ધકેલો. તમે ઉપરની તરફ એક ધક્કો અનુભવશો તેને હજુ વધારે અંદર તરફ ધકેલો. તમે તેને વધારે ઊંડાઈએ લઈ – જવામાં મુશ્કેલી અનુભવશો, જે દર્શાવે છે કે પાણી બૉટલ પર ઉપરની દિશામાં એક બળ લગાડેલ છે. જેમ જેમ બૉટલને પાણીમાં અંદરની તરફ ધકેલવામાં આવે છે તેમ તેમ તેની પર પાણી દ્વારા લાગતું બળ વધતું જાય છે, જ્યાં સુધી તે પૂરી ડૂબી ન જાય.
• હવે બૉટલને છોડી દો. તે ઉછળીને સપાટી પર પાછી આવે છે.
• શું પૃથ્વીનું ગુરુત્વાકર્ષણ બળ આ બૉટલ પર કાર્યરત છે? જો એમ હોય તો બૉટલને છોડી દેતાં તે પાણીમાં ડૂબતી કેમ નથી? તમે બૉટલને પાણીમાં કેવી રીતે ડુબાડશો?

ચર્ચા-વિચારણા: હા. પૃથ્વીનું ગુરુત્વાકર્ષણ બળ બૉટલ પર શિરોલંબ અધોદિશામાં લાગે છે.

→ હવે, બૉટલને છોડી દેતાં તે પાણીમાં ડૂબતી નથી, કારણ કે બૉટલ પર પાણી વડે શિરોલંબ ઊર્ધ્વદિશામાં લાગતું બળ, અધોદિશામાં લાગતા ગુરુત્વાકર્ષણ બળ કરતાં વધુ છે.
(કારણ કે, બૉટલ જ્યારે સંપૂર્ણપણે પાણીની અંદર હોય ત્યારે બૉટલ વડે સ્થળાંતરિત થતું પાણી બૉટલના કદ જેટલું હોય છે. તેથી સ્થળાંતરિત થયેલા પાણીનું વજન (બળ) જે શિરોલંબ ઊર્ધ્વદિશામાં હોય છે, તે બૉટલના વજન (બળ) કરતાં વધુ હોય છે.)

→ હવે, જો બૉટલને સંપૂર્ણપણે રેતીથી ભરી દેવામાં આવે અને પછી તેને પાણીમાં મૂકવામાં આવે, તો તે પાણીમાં ડૂબી જાય છે. અહીં બૉટલ પર અધોદિશામાં લાગતું ગુરુત્વાકર્ષણ બળ, પાણી વડે ઊર્ધ્વદિશામાં લાગતાં બળ કરતાં વધુ હોય છે.
(કારણ કે આ સ્થિતિમાં રેતી ભરેલી બૉટલનું વજન, બૉટલ વડે વિસ્થાપિત થયેલા પાણીના વજન કરતાં વધુ હોય છે.)

નિષ્કર્ષ: જો વસ્તુનું વજન (બળ), તેના પર પાણી વડે ઊર્ધ્વદિશામાં લાગતાં બળ કરતાં ઓછું હોય, તો તે પાણીની સપાટી પર તરે છે નહિ તો તે પાણીમાં ડૂબી જાય છે.

પ્રવૃત્તિ 10.5 [પા.પુ. પાના નં. 140]

• પાણીથી ભરેલ એક બીકર લો.
• એક લોખંડની ખીલી લો. તેને પાણીની સપાટી પર મૂકો.
• જુઓ શું થાય છે?

ચર્ચા-વિચારણા: ખીલી ડૂબી જાય છે.
(ખીલી પર લાગતું પૃથ્વીનું ગુરુત્વાકર્ષણ બળ તેને નીચેની તરફ ખેંચે છે. પાણી ખીલી પર ઉપ્લાવક બળ લગાડે છે, જે તેને ઉપરની દિશામાં ધકેલે છે. પરંતુ ખીલી પર નીચેની તરફ લાગતું બળ, ખીલી પર પાણી દ્વારા લાગતા ઉગ્લાવક બળ કરતાં વધારે છે. તેથી તે ડૂબી જાય છે.)

નિષ્કર્ષ: જ્યારે વસ્તુનું વજન (બળ), તેના પર પ્રવાહી (અહીં પાણી) વડે લાગતાં ઉપ્લાવક બળ કરતાં વધુ હોય, તો તે પ્રવાહીમાં (અહીં પાણીમાં) ડૂબી જાય છે.

પ્રવૃત્તિ 10.6 [પા.પુ. પાના નં 140].

• પાણીથી ભરેલ એક બીકર લો.
• એક ખીલી તથા સમાન દ્રવ્યમાન ધરાવતો એક બૂચ(Cork) લો.
• બંનેને પાણીની સપાટી પર મૂકો.
• જુઓ શું થાય છે?

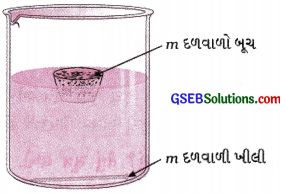
[આકૃતિ 10.6: પાણીની સપાટી પર મૂકેલ લોખંડની ખીલી ડૂબી જાય છે, જ્યારે બૂચ તરે છે.]

ચર્ચા-વિચારણા: બૂચ તરે છે જ્યારે ખીલી ડૂબી જાય છે. આમ થવાનું કારણ તેમની ઘનતાઓ વચ્ચેનો તફાવત છે. કોઈ પદાર્થની ઘનતા એટલે તેનું એકમ કદદીઠ દળ.
બૂચની ઘનતા પાણીની ઘનતા કરતાં ઓછી હોય છે. તેનો અર્થ 3 એ છે કે બૂચ પર પાણીનું ઉલ્લાવક બળ બુચના વજન કરતાં વધુ છે. તેથી તે તરે છે. જુઓ આકૃતિ 10.6.

લોખંડની ખીલીની ઘનતા પાણીની ઘનતા કરતાં વધારે છે. એનો અર્થ એ થયો કે લોખંડની ખીલી પર પાણીનું ઉપ્લાવક બળ ખીલીના વજન કરતાં ઓછું છે. તેથી તે ડૂબી જાય છે.
[બીજા શબ્દોમાં, અહીં બૂચ અને ખીલી બંનેના દળ સમાન છે પણ બૂચની ઘનતા ખીલીની ઘનતા કરતાં ઓછી હોવાથી બૂચનું કદ, ખીલીના કદ કરતાં વધુ છે.
જ્યારે બંનેને પાણીની સપાટી પર મૂકવામાં આવે છે ત્યારે બૂચ દ્વારા વિસ્થાપિત થયેલા પાણીનું કદ, ખીલી દ્વારા વિસ્થાપિત થયેલા પાણીના કદની સાપેક્ષે વધુ હોય છે. તેથી બૂચ પર પાણી વડે લાગતું ઉલ્લાવક બળ, ખીલી કરતાં વધુ છે.]

નિષ્કર્ષ: પ્રવાહીની ઘનતા કરતાં ઓછી ઘનતા ધરાવતાં દ્રવ્યો ૨ (પદાર્થો) તે પ્રવાહી પર તરે છે અને પ્રવાહી કરતાં વધારે ઘનતા ધરાવતાં દ્રવ્યો (પદાર્થો) ડૂબી જાય છે.

પ્રવૃત્તિ 10.7 [પ.પુ. પાના નં. 141]

• એક પથ્થરનો ટુકડો લો અને તેને એક છેડેથી રબરની દોરી કે સ્વિંગ બૅલેન્સ સાથે બાંધો.
• આકૃતિ 10.7 (a)માં દર્શાવ્યા પ્રમાણે સ્પ્રિંગ બૅલેન્સ કે રબરની દોરીને પકડીને પથ્થરને લટકાવો.
• પથ્થરના વજનને કારણે રબરની દોરીની લંબાઈમાં થતો વધારો અથવા સ્પ્રિંગ બૅલેન્સનું વાંચન નોંધી લો.
• હવે પથ્થરને એક વાસણમાં રાખેલા પાણીમાં આકૃતિ 10.7 (b)માં દર્શાવ્યા પ્રમાણે ધીરે ધીરે ડુબાડો.
• રબરની દોરીની લંબાઈમાં અથવા સ્પ્રિંગ બૅલેન્સના વજનમાં શું ફેરફાર થાય છે તે નોંધો.

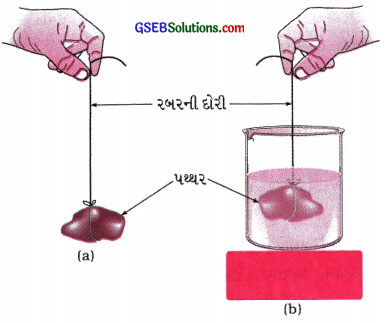
[આકૃતિ 10.7: (a) હવામાં લટકાવેલ પથ્થરના ટુકડાના વજનને કારણે રબરની દોરીની લંબાઈમાં વધારો થાય છે.
(b) પથ્થરને પાણીમાં ડુબાડતાં રબરની દોરીની લંબાઈના વધારામાં ઘટાડો થાય છે.]

ચર્ચા-વિચારણા:
1. કિસ્સા (b)માં રબરની દોરીની લંબાઈમાં થતો વધારો કિસ્સા (a)માં થતાં વધારા કરતાં ઓછો છે.

2. પથ્થરને ધીમે ધીમે જેમ જેમ પાણીમાં નીચેની તરફ લઈ જવામાં આવે છે તેમ તેમ રબરની દોરીની લંબાઈમાં અથવા બૅલેન્સના અવલોકનમાં ઘટાડો થાય છે.

3. જ્યારે પથ્થર પાણીમાં સંપૂર્ણ ડૂબી જાય છે. ત્યારબાદ અવલોકનમાં કોઈ ફેરફાર થતો નથી અને તે વખતે બૅલેન્સનું અવલોકન લઘુતમ હોય છે.

4. હવે, જો પથ્થરને હજી પણ પાણીની અંદર લઈ જવામાં – આવે તો બૅલેન્સના અવલોકનમાં કોઈ ફેર પડતો નથી.

5. કિસ્સા (a)માં રબરની દોરીની લંબાઈમાં થતો વધારો કે સ્વિંગ બૅલેન્સના અવલોકનમાં થતો વધારો પથ્થરના વજન (mg)ને – લીધે છે.
પથ્થરને પાણીમાં ડુબાડતાં (કિસ્સો (b)) રબરની દોરીની લંબાઈમાં – થતા વધારામાં ઘટાડો થાય છે. (અથવા સ્પ્રિંગ બૅલેન્સના અવલોકનમાં : ઘટાડો થાય છે.) તેનું કારણ પાણીમાં પથ્થરના વજનમાં થતો ઘટાડો છે. પાણીમાં પથ્થરના વજનમાં થતો આ ઘટાડો પથ્થર પર ઉપરની દિશામાં લાગતાં કોઈક બળને લીધે છે. તેના પરિણામસ્વરૂપ રબરની : દોરી પર લાગતાં પરિણામી (કુલ) બળમાં ઘટાડો થાય છે.
આ કોઈક બળને ઉલ્લાવક બળ કહે છે.

[બીજી રીતે વિચારતાં પથ્થરને પાણીમાં ડુબાડતાં તેના દેખીતા વજન(Apparent weight)માં ઘટાડો થાય છે. જ્યારે પથ્થર પાણીમાં સંપૂર્ણ ડૂબી જાય છે ત્યારે આ દેખીતું વજન સૌથી ઓછું હોય છે. આ વજનમાં થતો દેખીતો ઘટાડો પાણી દ્વારા પથ્થર પર લાગતાં ઉપ્લાવક બળને લીધે છે. પથ્થર પાણીમાં સંપૂર્ણ ડૂબે નહીં ત્યાં સુધી ઉપ્લાવક બળનું મૂલ્ય, (પથ્થરની) ઊંડાઈ સાથે વધતું જાય છે.]