GSEB Class 10 Maths Notes Chapter 7 Coordinate Geometry

This GSEB Class 10 Maths Notes Chapter 7 Coordinate Geometry covers all the important topics and concepts as mentioned in the chapter.

Coordinate Geometry Class 10 GSEB Notes

You have studied that to locate the position of a point on a plane, we require a pair of coordinate aies. The distance of a point from the y-axis is called its x-coordinate, or abscissa. The distance of a point from the x-axis is called its y-coordinate, or ordinate. The coordinates of a point on the x-axis are of the form (x, 0) and of a point on the y-axis are of the form (0, y).

Also, you have seen that a linear equation in two variables of the form ax + by + c = 0, a, b are not simultaneously zero), when represented graphically, gives a straight line. Further in Chapter IV, you have seen the graph of y = ax² + bx + c (a ≠ 0), is a parabola. In fact, coordinate geometry has been developed as an algebraic tool for studying geometry of figures. It helps us to study geometry using algebra, and understand algebra with the help of geometry. Because of this, coordinate geometry is widely applied in various fields such as physics, engineering, navigation, seismology and art.

Distance Formula
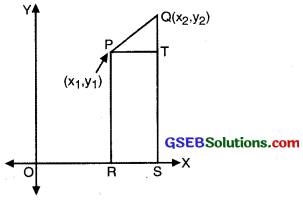
Let us now find the distance between any two points P (x₁, y₁ ) and Q (x₂, y₂). Draw PR and QS perpendicular to the x-axis. A perpendicular from the point P on QS is drawn to meet it at point T (see fig.)
Then, OR = x₁, OS = x₂.
So, RS = x₂ – x₁ = PT
Also, SQ = y₂, ST = PR = y₁

So, QT = y₂ – y₁
Now, applying the Pythagoras theorem in ∆PTQ, we get:
PQ² = PT² + QT²
=(x₂ – x₁)² + (y₂ – y₁)²
Therefore, PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Note that since distance is always non-negative, we take only the positive square root. So, the distance between the points P (x₁; y ₁) and Q (x₂, y₂) is:
PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
which is called the distance formula.

Remarks:

• In particular, the distance of a point P (x, y) from the origin O (0, 0) is given by
  OP = \(\sqrt{x^{2}+y^{2}}\)
• We can also write,
  PQ = \(\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}\)

Section Formula
Consider any two points A (x₁, y₁) and B (x₂, y₂) and assume that P (x, y) divides AB internally in the ratio m₁: m₂, i.e.,
\(\frac{\mathrm{PA}}{\mathrm{PB}}=\frac{m_{1}}{m_{2}}\) (see fig.)

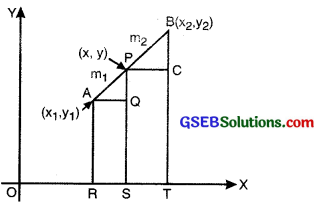
Draw AR, PS and BT perpendicular to the x- axis. Draw AQ and PC parallel to the x-axis. Then, by the AA similarity criterion,
∆PAQ ~ ∆BPC
Therefore, \(\frac{\mathrm{PA}}{\mathrm{PB}}=\frac{\mathrm{AQ}}{\mathrm{PC}}=\frac{\mathrm{PQ}}{\mathrm{BC}}\) ……….(1)

Now, AQ = RS = OS – OR = x – x₁
PC = ST = OT – OS = x₂ – x
PQ = PS – QS = PS – AR = y – y₁
BC = BT – CT = BT – PS = y₂ – y

Substituting these values in (1), we get:

So, the coordinates of the point P (x, y) which divides the line segment joining the points A (x₁, y₁) and B (x₂, y₂), internally, in the ratio m₁: m₂ are:
\(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\) …………(2)

This is known as section formula.
This can also be derived by drawing perpendiculars from A, P and B on the y-axis and proceeding as above.

If the ratio in which P divides AB is k: 1, then the coordinates of the point P will be
\(\left(\frac{k x_{2}+x_{1}}{k+1}, \frac{k y_{2}+y_{1}}{k+1}\right)\)

Special Case: The mid-point of a line segment divides the line segment in the ratio 1:1. Therefore, the coordinates of the mid-point P of the join of the points A (x₁, y₁) and B (x₂, y₂) is
\(\left(\frac{1 . x_{1}+1 . x_{2}}{1+1}, \frac{1 . y_{1}+1 . y_{2}}{1+1}\right)=\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

Area of a Triangle
In your earlier classes, you have studied how to calculate the area of a triangle when its base and corresponding height (altitude) are given. Your have used the formula:
Area of a triangle = \(\frac{1}{2}\) × base × altitude.

Let ABC be any triangle whose vertices are A (x₁, y₁), B(x₂, y₂) and C (x₃, y₃). Draw AP, BQ and CR perpendiculars from A, B and C, respectively, to the x-axis. Clearly ABQP, APRC and BQRC are all trapezia (see Fig.).

Now, from Figure it is clear that
area of ∆ABC area of trapezium ABQP + area of trapezium APRC – area of trapezium BQRC.

Your also know that the
area of a trapezium – \(\frac{1}{2}\) (sum of parallel sides) (distance between them)
Therefore,

Thus, the area of AABC is the numerical . value of the expression
\(\frac{1}{2}\)[x₁ (y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]