This GSEB Class 12 Commerce Statistics Notes Part 1 Chapter 1 Index Number Posting covers all the important topics and concepts as mentioned in the chapter.
Index Number Class 12 GSEB Notes
Objective:
To enable the students to be acquainted with the basic study of changes in price, value or quantity with reference to change in time.
Definition and Meaning of Index Number:
Relative Change:
The ratio of change in value of variable quantity at two different time periods is known as Relative Change. It is denoted by symbol I.
For example, if production for item A in the years 2016 and 2017 are 120 tons and 150 tons respectively, then the relative change in production for the year 2017 compared to the year 2016 is \(\frac{150}{120}\) = 1.25.
Index Number:
The measure which shows the relative percentage change in the variable quantity is known as Index Number. In the above illustration, Index Number of production of item A for year 2017 = 1.25 × 100 = 125. Thus, “The percentage relative change in the value of a variable quantity related with an item for given (current) period compared to its value in the fixed (base) period is called an Index Number.”
Price Index Number:
- The relative change in prices of each item at two different points of time expressed in percentage is called Price Index Number.
- If price for the item A for years 2016 and 2017 are denoted by p0 and p1 respectively then Price relative (I) = \(\frac{p_{1}}{p_{0}}\) and Price Index Number = I × 100 = \(\frac{p_{1}}{p_{0}}\) × 100.
Quantity Index Number:
- The relative percentage change in quantity of each item at two different points of time is called Quantity Index Number.
- If quantity for the item A for years 2016 and 2017 are denoted by q0 and q1 respectively then Quantity relative = \(\frac{q_{1}}{q_{0}}\) and Quantity Index Number = \(\frac{q_{1}}{q_{0}}\) × 100.
General Index Number:
The average of the percentage change in the value of a variable associated with one or more items for the current period compared to its value in the fixed (base) period is called a general index number for the group.
Characteristics of Index Number:
- Index number is a relative measure showing the percentage change in the values of variable.
- It is a measure independent of unit of measurement.
- It is a comperative measure.
- It compares the situations prevailing at two different points of time by means of ratio.
- It is a special average. Hence, it posseses all the qualities of the average.
- It is a weighted average.
![]()
Uses of Index Number:
1. Price Index Number is used to determine the purchasing power of money at a given point of time.
2. To convert the current monetary values of the different activities of the country like agricultural production, industrial and small industries production and national domestic production into real values.
3. It is used to study the overall conditions prevailing in business and trade of the country.
4. Uses of different Index Numbers:
- Wholesale Price Index Number: It is used to study the changes in the price level of the country.
- Cost of Living Index Number: It is used by the government to determine pay scales, dearness allowances, bonus, etc. of government employees and to devise taxation policy.
- Index Number of National Income: To determine the targets for the five year plans and to evaluate the economic condition of the country.
- Index Number for Agricultural Production: It helps the government to devise suitable agricultural policies and to verify whether the farmers get appropriate prices for their agricultural products or not.
- Index Number of Import-Export: It is used to determine export-import policy foreign exchange requirement and to stipulate norms for taxations on goods to be imported and exported.
- Index Number of Industrial Productions: It is useful to study the changes occurring in production in industries and manufacturing units and also to business houses in planning of trading and industrial activities in the country.
- Index Number for Employment: It provides the picture of employment prevailing in the country as well as it is helpful to the government for manpower planning.
- Index Number for Capital Investments: It is used to study the changes in prices of shares and stock as well as the mobility of investments.
- Index Number of Raw Materials: It is used for assessing the feasibilities of importing as well as exporting raw materials.
- Index Number of Human Development: It is useful to determine the state of human resource, standard of living, life expectancy and level of education.
- Index Number of Trade: It provides useful guidance to study the general situation of economic activities of business and trade in the country.
Base Year:
1. Base Year:
When the changes in the price, of an item are compared with the price of the same item in the fixed period of past then that fixed period is called the Base Year.
2. Current Year:
The year for which the prices of the items are to be compared with the prices of the base year is called the Current Year.
3. Methods for Selection of Base Year:
- Fixed base method
- Chain base method
Conversion of Base Year:
- Conversion from Fixed Base Index Number to Chain Base Index Number: To know the short-term changes in the values of a variable, such conversion is done.
- Conversion from Chain Base Index Number to Fixed Base Index Number: When the value of the variable at a given period is to be compared with the value of another period in a series of values of the variable it become necessary to convert the chain base index number into the fixed base.
Computation of Index Number:
When the information regarding the prices and quantities of consumption of different items are given
- Laspeyre’s Formula: The base year expenditure p0q0 is assigned as weight of the price relatives \(\frac{p_{1}}{p_{0}}\). It is denoted by symbol IL.
- Paasche’s Formula: The expenditure p0q1 of an item is assigned as the weight of the price relatives \(\frac{p_{1}}{p_{0}}\). It is denoted by the symbol Ip.
- Fisher’s Formula: The geometric mean of Laspeyre’s and Paasche’s index numbers is called Fisher’s index number and it is denoted by the symbol IF. Fisher’s index number is called an Ideal index number.
Reasons for an Ideal Index Number:
- The formula for Fisher’s index number takes into account the prices and quantities of both, the base year as well as the current year.
- It is defined as the geometric mean which is considered to be the best average for the index number.
- It satisfies the basic tests of a good index number.
- It is not biased because it balances the drawbacks of Laspeyre’s and Paasche’s index number.
Cost of Living Index Number:
The number showing the percentage relative changes in the cost of living of the people of a certain section of the society in the current year as compared to the base year is called the cost of living index number.
1. Points for the Construction of Cost of Living Index Number:
- Purpose,
- Family budget inquiry,
- Price quotations of the commodities,
- Selection of the base year,
- Selection of the average and
- Selection of the weight.
Weight:
The number showing the importance assigned to different items selected for the construction of an index number according to their importance is called weight.
Types of Weight:
- Implicit Weight: This is an indirect method of assigning weights. It is implied in the selection of items. It cannot be expressed in number.
- Explicit Weight: This is a direct method of assigning weights. Such weights are determined according to importance of the items. It can be expressed in numbers.
There are two popular methods of assigning explicit weights:
- Aggregate expenditure method and
- Family budget method.
2. Uses of Cost of Living Index Number:
- It represents the economic condition of the class of people for whom it is constructed.
- It is useful to find the real purchasing power of money for the concerned class of people.
- It is useful to fix the standards of living for different classes of people.
- It also gives some idea about what special amenities should be provided to different classes of people.
- It facilitates government in devising policies in matters of taxation and price control.
3. Limitation of Cost of Living Index Number:
- It represents the average changes of the entire class but it cannot be used, for a particular person of that class.
- It is based on the Impractical assumption that levels of consumption of quantities of different items of the base year are also maintained in the current year.
- Problem arises in assigning weights to different items as the consumptions made by the people of same class are in different proportion.
- The cost of living index number obtained for a particular class of people in a region cannot be used for the same class of people in some other region.
- It represents the average percentage change in the cost of living of the people of any class of the society. So the individual expenditure for the cost of living cannot be measured.
- For different class of people of the society and for different region separate index numbers are to be constructed.
![]()
Important Formulae
1. Price relative:
Price relative = \(\frac{p_{1}}{p_{0}}\)
Where, p1 = Current year’s price
p0 = Base year’s price
2. Quantity relative:
Quantity relative = \(\frac{q_{1}}{q_{0}}\)
Where, q1 = Current year’s quantity
q0 = Base year’s quantity
3. Index number:
I = \(\frac{p_{1}}{p_{0}}\) × 100 ⇒ Price relative × 100
4. General index number of a group:
Price relative = \(\frac{p_{1 i}}{p_{0 i}}\) i = 1, 2, 3, …, n
I = \(\frac{\Sigma\left(\frac{p_{1 i}}{p_{0}}\right)}{n}\) × 100
Where, p1i = Current year’s price of ith item
p0i = Base year’s price of ith item
n = No. of items in group
5. Index number on basis of price relatives of n items:
I = \(\frac{\Sigma\left(\frac{p_{1 i}}{p_{0}}\right)}{n}\) × 100
6. Index number by fixed base method:

7. Index number by chain base method:

8. Change of Base:
1. To convert fixed base index number into chain base index number:

2. To convert chain base index number into fixed base index number:

9. Laspeyre’s formula:
IL = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) × 100
10. Paasche’s formula:
IF = \(\sqrt{\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}} \times \frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}}\) × 100
Or
IF = \(\sqrt{\mathrm{I}_{\mathrm{L}} \times \mathrm{I}_{\mathrm{P}}}\)
11. Fisher’s formula:
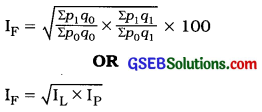
In the above formulae,
P0 = Price of the base year
q0 = Quantity of the base year
P1 = Price of the current year
q1 = Quantity of the current year
12. Cost of living Index number:
1. Aggregate expenditure method:
(i) Index number = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\)
Where, Σp1q0 = Total expenditure of current year
Where, Σp0q0 = Total expenditure of base year
[Note: This is Laspeyre’s Index number.]
(ii) Index number = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) × 100
Where, Σp1q1 = Total expenditure of current year
Σp0q0 = Total expenditure of base year corresponding to quantity of current year
[Note: This is Paasche’s Index number.]
2. Family budget method:
Index number = \(\frac{\Sigma \mathrm{IW}}{\Sigma \mathrm{W}}\)
Where, I = \(\frac{p_{1}}{p_{0}}\) × 100
W = p0q0 = Expenditure of base year
[Note: In the formula, if we replace, Pi
W = p0q0 > I = \(\frac{p_{1}}{p_{0}}\) it is Laspeyres Index number.]
13. Real wage:
Real wage = \(\frac{\text { Wage }}{\text { cost of living index number }}\) × 100
14. Purchasing power of Money:
Purchasing power of Money = \(\frac{1}{\text { cost of living index number }}\) × 100
15. Rate of Inflation:

![]()
Remember for the Construction of Index Number
1. Index number is independent of units. Hence, it should not be stated that the index number of price is ₹ 350. But it should be stated that the index number of price is 350.
2. Index number of the base year is always 100.
3. Adding to 100, the percentage rise in the variate value in the current year as compared to the base year, we get the index number of that variate for the current year, e.g., if the price of certain commodity in the current year has increased by 140% with respect to the price of the commodity in the base year, then the index number of price for that commodity is 100 + 140 = 240.
4. Subtracting from 100, the percentage fall in the variate value in the current year as compared to the base year, we get the index number of that variate for the current year, e.g., if the production of certain commodity in the current year has decreased by 8 % with respect to the production in the base year, then the index number of production for that commodity is 100 – 8 = 92.
5. Multiplying by 100, the number representing what multiple of the variate value in the base year is the variate value in the current year, we get the index number of that variate for the current year, e.g., if the expense on food in the current year is 1\(\frac{1}{2}\) times the expense on food in the base year, then the index number of the expense on food for the current year is 100 × 1\(\frac{1}{2}\) = 100 × 1.5 = 150.
6. For the calculations of Laspeyre’s, Paasche’s and Fisher’s index number, prepare the four columns P1q0’ P0q0’ P1q1, and P0q0 respectively.
7. If the price of two different periods and weights are given or if the price of two different periods and percentage expenses for different items are given, then calculate the index number by family budget method only.
8. If the column of ‘unit’ is given in the data, it represents that the price of the item is given in that unit. Before starting the calculation for the index number, check whether the units of the price and quantity are same or not. If they are not the same, make them to be the same and then only start the calculations.