This GSEB Class 6 Maths Notes Chapter 6 Integers covers all the important topics and concepts as mentioned in the chapter.
Integers Class 6 GSEB Notes
Introduction:
We have already learnt about whole numbers, i.e. 0, 1, 2, 3, 4, 5, 6, which is the extension of natural numbers. We have studied in whole number system that sum of two whole numbers is always a whole number, but difference of two whole numbers is not always a whole number. But what is 6 – 9 = ?. To answer this problem we need to extend our number system from whole numbers to integers.
Negative Numbers:
- Negative number is a real number less than zero. Negative numbers represent opposite to the positive numbers. If positive represents a movement to the right, then negative represents a movement to the left.
- Negative numbers are usually written with a minus sign in front of number like -1 (pronounced as minus one or negative one). Numbers less than zero are negative and greater than zero are positive. Zero itself is neither positive nor negative. Zero is non-negative non-positive number.
Integers:
We know + 1, is one more than 0 and – 1, is one less than 0.
( + 1) + (- 1) = 0. – 1 and + 1 are called opposite of each other.
Similarly, 2 + ( – 2) = 0. – 2 and 2 called opposite of each other and so on.
A collection of numbers which consists of positive numbers (i.e., natural numbers), zero and negative numbers (i.e., negative natural numbers) i.e., -3, – 2, – 1, 0,1, 2, are called integers.
- The numbers 1,2, 3,……….. i.e., natural numbers are called positive integers.
- The numbers – 1, – 2, – 3, ……..are called negative integers.
- The number 0 is simply an integer. 0 is neither positive nor negative.
N : {1,2, 3, 4, 5, }
W: {0, 1,2, 3, 4, 5, }
Z or I: { ,-5,-4,-3,-2,-1,0, 1, 2, 3, 4, 5,…… }
Remark. We use the symbol to denote negative integers.
![]()
Representation of Integers on Number Line:
Since negative integers are opposite of positive integers, we represent them in the opposite direction i.e., on the left side of zero on the number line. The opposite integers, e.g., 4 and – 4 are kept at the same distance from zero which is regarded as neither positive nor negative. Hence, we have the integers on the number line as shown :
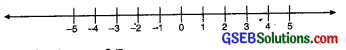
Ordering of Integers
We know that, in whole numbers, a number is greater than the other if the first lies to the right of the second, on the number line. This idea can be well extended to integers.
Some important observations are :
- Every integers has its successor as well as predecessor.
- Every positive integer is greater than 0 and every negative integer is less than 0.
- The greater integer between the two given integers is the lesser integer between the negative of these integers e.g. 8 > 5 but -8 < -5.
- A number farther from 0 on the right has larger value.
- A number farther from 0 on the left side has smaller value.
- Smallest positive integer is 1 but largest positive integer (or just integer) is not possible to write in.
- Largest negative integer is ‘-V but smallest negative integer (or just integer) is not possible to write in.
- 0 is neither positive integer nor negative integer.
- Every positive integer is greater than every negative integer.
- 0 is greater than all negative integers. In other words, if a and b are two integers such that a > b, then – a < -b.
Addition of Integers:
We know how to add two whole numbers. Since each whole number is either a positive integer or zero, we can add the integers if they are positive or zero. We shall extend the method of addition of whole numbers on number line to the integers.
Notes:
- Adding ‘- a’ to a number means ‘move a steps to the left of the number.’
- Adding ‘a’ to a number means ‘move a steps to the right of the number.’
Properties of Addition of Integers
- If a, b are integers, then a + b is an integer.
- If a, b are integers, then a + b = b + a.
- If a, b and c are three integers, then a + (b + c) = (a + b) + c.
- For any integer a, a + 0 = 0 + a = a.
- Every integer has a successor and also every integer has a predecessor
![]()
Subtraction of Integers:
Subtraction is a process which is inverse to that of addition.
Additive Inverse (Negative). For each non-zero integer, a, there is an integer – a such that a + ( – a) = 0. ‘ – a’ is called the negative (or additive inverse) of a.
Note: Negative of zero is zero itself.
Rule:
If a and b two integers, to subtract b from a, we change the sign of b and add it to a. i.e a – b = a + ( – b) We find the value of an expression containing various terms with plus and minus signs as follows : ,
- Step 1 We add all terms with plus ( + ) sign together.
- Step 2 We add all terms with minus ( – ) sign together.
- Step 3 We find the difference of the absolute values of the two sums obtained in step 1 and step 2.
- Step 4 We assign to the result of step 3 the sign of sum having larger absolute value.
Properties of Subtraction
- If a and b are two integers and a – b = c, then c must be an integer.
- If a is any integer, than ‘a – 1’ is its predecessor.
- If a is an integer, than a – 0 = a.