This GSEB Class 7 Maths Notes Chapter 11 Perimeter and Area covers all the important topics and concepts as mentioned in the chapter.
Perimeter and Area Class 7 GSEB Notes
Perimeter: Perimeter of a simple closed figure is the length of its boundary. Its units are same as the units of length i.e., cm and m etc.
Area: Area of a simple closed figure is the measure of the surface enclosed in it. Units of area are cm and m2 etc.
Perimeter and area of a Rectangle and a Square
Rectangle: Let us consider a rectangle ABCD with length = l units and breadth = b units
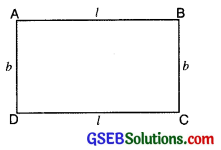
Then, Perimeter of rectangle
= AB + BC + CD + DA
= l + b + l + b
= 2l +2b
= 2 (l + b) units
Area of rectangle = (Length × Breadth) sq. units
length and breadth can be found by using the formula
Length = \(\frac{\text { Area }}{\text { Breadth }}\) units
and Breadth = \(=\frac{\text { Area }}{\text { Length }}\) units
Square: Let us consider a square ABCD having each side equal to a units then,
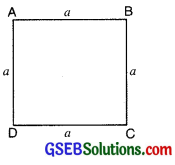
Perimeter of square
= AB + BC + CD + DA
= a + a + a + a
= 4a units
= (4 × side) units
Area of square = Side × Side
A = a × a
A = a2 sq. units.
Triangles as Parts of a Rectangle
Let a rectangle ABCD of length 10 cm and breadth 6 cm. Draw a diagonal of the rectangle; It divides the rectangle into two triangles and sum of the area of two triangles is equal to the area of rectangle.
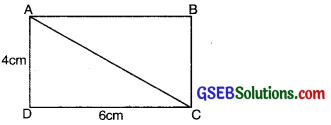
i.e., Area of ∆ABC + Area of ∆ACD = Area of Rectangle ∆BCD
∴ Area of each triangle
= \(\frac{1}{2}\) × area of rectangle
= \(\frac{1}{2}\) × Length × Breadth
= \(\frac{1}{2}\) × 6 × 4
= 24 cm2
If we divide the rectangle into 4 triangles, then also the result is same i.e. sum of area of triangles is equal to the area of rectangle.
![]()
Triangles as Parts of a Rectangle
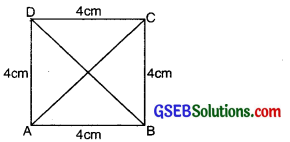
Let a Square ABCD of side 4 cm is divided into four triangles as shown in the figure. Then Area of ∆AOB + Area of ∆BOC + Area of ∆COD + Area of ∆DOA = Area of square ABCD
1
= Area of each triangle = \(\frac{1}{4}\) × Area of square
= \(\frac{1}{2}\) × (Side)2
= \(\frac{1}{2}\) × 4 × 4 = 4 cm2
Generalising for other Congruent Parts of Rectangles
A rectangle of length 9 cm and breadth 7 cm is divided into two parts, congruent to each other.
Area of each congruent part = \(\frac{1}{2}\) × Area of Rectangle ABCD
= \(\frac{1}{2}\) × Length × Breadth
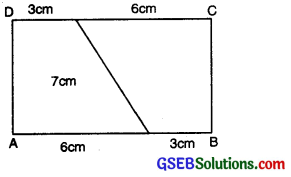
= \(\frac{1}{2}\) × 9 × 7
= 31.5 cm2.
Area of Parllelogram
A quadrilateral in which each pair of opposite sides is parallel and equal is called a parallelogram. In the figure, we see that the length of the rectangle ANMB is equal to the base of parallelogram ABCD and the breadth of the rectangle is equal to the height of parallelogram.
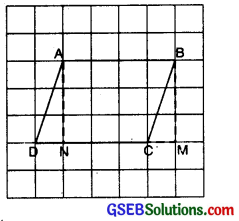
Area of parallelogram = Area of Rectangle
Area of parallelogram = Length × Breadth
Area of parallelogram = Base × Height
From above, we also have the following relationship
Base = \(\frac{\text { Area of Parallelogram }}{\text { Height }}\)
or
Height = \(\frac{\text { Area of Parallelogram }}{\text { Base }}\)
[Length of Rectangle = Base of Parallelogram
Breadth of Rectangle = height of Parallelogram]
Area of a Triangle
A closed plane figure made by joining three line segments is called a triangle,
(a) In a scalene triangle all the three sides have differnt lengths. If base and corresponding altitude ar given.
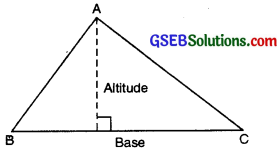
The area of ∆ = \(\frac{1}{2}\) × (base × height) sq. units
(b) In a right angled triangle, the side opposite to the right angle is called the hypotenuse, the adjacent sides to right angle are called legs.
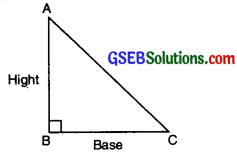
The area of right angled triangle
= \(\frac{1}{2}\) × (base × height) sq. unit.
Circle
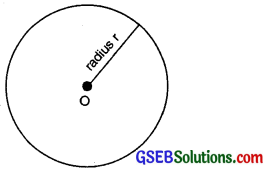
A circle is a simple closed curve consisting of all those points in a plane each of which is at a constant distance from a fixed point O inside it. Let this constant distance be r.
(a) The fixed point O is called the centre of the circle.
(b) Line segment joining any point on the circle to its centre is called the radius of the circle. It is denoted by r.
(c) A line segment joining any two points of a circle is called the chord of the circle.
(d) A chord passing through the centre of the circle is known as the diameter of circle. It is denoted by d.
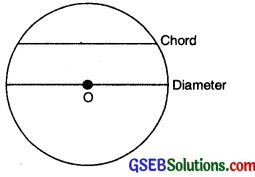
Circumference of circle. The perimeter of a circle is called its circumference.
Circumference of a circle = Measure of the boundary of a circle.
Conversion of units:
| Length units | Area Units |
| 1 cm = 10 mm | 1 cm2 = (10 × 10) mm2 = 100 mm2 |
| 1 dm = 10 cm | 1 dm2 = (10 × 10) cm2 = 100 cm2 |
| 1 m = 10 dm | 1 m2 = (10 × 10) dm2 = 100 dm2 |
| 1 m = 100 cm | 1 m2 = (100 × 100) cm2 = 10000 cm2 |
| 1 dam = 10 m | 1 dam2 = (10 × 10) m2 = 100 m2 |
| 1 hm = 100 m | 1 hm2 (100 × 100) m2 = 10000 m2 |
| 1 km = 100 m | 1 km2 = (1000 × 1000) m2 = 1000000 m2 |
| 1 are = 100 m2 | |
| 1 hectare = 10000 m2 |
![]()
Area of Paths, Cross Roads and Borders:
In this section, you will learn how to apply the formulae for the areas of rectangle and a square to determine the areas of the paths around (outside or inside) a rectangle and also of the central paths. The knowledge of this concept can be applicable m daily life problems such as cost of printing border on the four sides of a saree, cost of cementing a verandah constructed all around a school building etc.
Let us consider the following types of figures which will work as stepping stone in understanding and solving the problems related to the rectangular paths.
I. Area of shaded portion
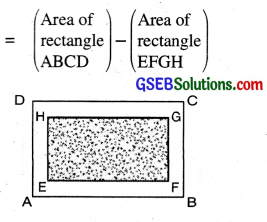
II. Area of shaded portion
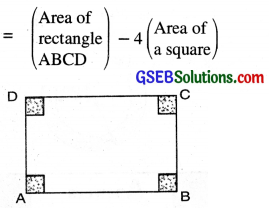
III. Area of shaded portion
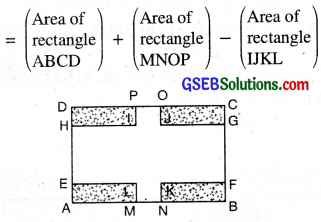
Note: If IJ = JK
IJKL will be a square.