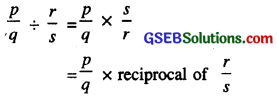This GSEB Class 7 Maths Notes Chapter 9 Rational Numbers covers all the important topics and concepts as mentioned in the chapter.
Gujarat Board Class 7 Maths Notes Chapter 9 Rational Numbers
1. Natural numbers: Counting numbers 1, 2, 3, 4 ……….. etc. are called natural numbers.
Set of natural numbers is denoted by N.
2. Whole numbers: The number ‘zero’ (0) together with natural numbers gives the numbers 0,1, 2, 3 which are called whole numbers.
The set of whole numbers is denoted by W where W = {0, 1, 2, 3, 4, 5 ….}
3. Integers: Integers are the extension of whole numbers.
The numbers …………..- 3, – 2, – 1, 0, 1, 2, 3……….. are integers. The numbers 1, 2, 3……… are called positive integers.
The numbers ………- 3, – 2, – 1 are called negative integers.
‘0’ is an integer neither positive nor negative.
Set of integers is denoted by Z,
Where Z = {………………-3, -2, -1, 0, 1, 2, 3…………….}
4. Need for rational numbers:
We have learnt to solve simple equations in one variable. We have integer ; 2 as solution of 2x – 4 = 0 and fraction; \(\frac{3}{2}\) as a solution of 2x – 3 = 0. But no integral or fractional value of x satisfies the equation 2x + 3 = 0.
So, we need to extend our number system (of integers and fractions) to include numbers in which equations like this may have solutions.
5. Rational numbers: Let us extend the system of fractions and consider the numbers of form \(\frac{p}{q}\) where p and q are any integers, but q is always non-zero. Thus, we consider all integers, all fractions and all ‘fraction like numbers’ such as
\(\frac{-4}{3}, \frac{3}{-4}, \frac{13}{-9}, \frac{16}{2}, \frac{-28}{-51}, \frac{0}{100}\) etc.
However, we donot include ‘numbers’ like \(\frac{5}{0}, \frac{97}{0}\) where zero is in the denominator. Such extended numbers are called the system of rational numbers. Thus a rational number is a number of form \(\frac{p}{q}\) where p and q are integers and q ≠ 0.
Integers are regarded as rational.
For example ; integers 100, – 6, 0 etc. are rational numbers, because these can be expressed as \(\frac{100}{1}, \frac{-6}{1} \text { and } \frac{0}{1}\) respectively.
6. Equivalent rational numbers:
Two rational numbers \(\frac{p}{q}\) and \(\frac{r}{s}\) are said to be equivalent if p × s = r × q.
Thus rational numbers \(\frac{-2}{3}, \frac{-4}{6}, \frac{10}{-15}\) are equivalent rational numbers.
For given rational number ; equivalent rational numbers can be obtained by denominator of given rational number by the same nonzero integer. Thus if is \(\frac{p}{q}\) a rational number, then \(\frac{2p}{2q}\) is also a rational number equivalent to \(\frac{p}{q}\)
7. Positive and Negative Rational numbers:
1. Rational number \(\frac{p}{q}\) whose numerator; p and denominator ; q are positive integers or p and q are both negative integers is a positive rational number.
So, \(\frac{3}{8}, \frac{5}{7}, \frac{2}{9}\) etc. are positive rational numbers.
2. Rational number ; \(\frac{p}{q}\) whose numerator p or denominator ; q is a negative integer is called a negative rational number. So, \(\frac{-5}{7}, \frac{-9}{5}, \frac{8}{-3}\) are negative rational numbers.
Note:
(a) The number 0 is neither a positive nor a negative rational number.
(b) \(\frac{-2}{-5}, \frac{-5}{-3}\) etc. are positive integers.
![]()
8. Rational numbers on a number line:
You know that while marking integers on the number line they are marked at equal distances from each other. Also, from 0, the distances of 1 and -1, 2 and -2, 3 and -3 etc. are same.
Let us draw one such number line.

In the same way, the rational numbers \(\frac{1}{2}\) and – \(\frac{1}{2}\) would be at same distance from 0. We know how to mark the rational number \(\frac{1}{2}\) . It is marked at a point which is half distance between 0 and 1. So – \(\frac{1}{2}\) would be marked at a point half the distance between 0 and -1.

To mark the rational number –\(\frac{3}{2}\), we first mark \(\frac{3}{2}\) on the right of 0. Let us first know, as to between which two integers these number lie. For this we write them as rational number with denominator 2. We have, 0 = \(\frac{0}{2}, \frac{1}{2}, \frac{2}{2}\) = 1, \(\frac{3}{2}, \frac{4}{2}\) = 2 and \(\frac{-1}{2}, \frac{-2}{2}\) = -1, \(\frac{-3}{2}, \frac{-4}{2}\) = -2
This shows that, \(\frac{3}{2}\) lies between 1 and 2 whereas – \(\frac{3}{2}\) lies between – 1 and – 2.
The number \(\frac{3}{2}\) lies halfway between 1 and 2 so – \(\frac{3}{2}\) would lie halfway between -1 and -2.

Mark \(\frac{-5}{2}\) and \(\frac{-7}{2}\) in a similar way.
Let rational numbers \(\frac{4}{7}\) and \(\frac{-6}{7}\) are marked on the number line as follows P represents \(\frac{4}{7}\) and Q represents \(\frac{-6}{7}\)

The rational numbers with different denominators can be represented in a simlar way.
9. Simplest or Lowest form of a rational number:
A rational number ; \(\frac{p}{q}\) (q ≠ 0) is said to be in the simplest or lowest form if p and q have no common factor other than 1 or that of the H.C.F. of p and q is 1.
The rational number; \(\frac{3}{7}, \frac{-103}{5}, \frac{19}{-115}\) are all rational numbers in the lowest form.
10. Standard form of a rational number: A rational number in the lowest form is said to be in the standard form if its denominator is positive.
For example. Rational numbers
\(\frac{3}{5}, \frac{-5}{8}, \frac{2}{7}, \frac{-7}{11}\) are in the standard form.
11. Comparison of rational numbers:
From a number line it is clear that:
- A positive rational number is always greater than zero.
- A negative rational number is always less than zero.
- If both the rational number are either positve or negative then they are compared as follows.
- Express each of the rational number with a positive denominator.
- Take L.C.M. of the denominators to make the denominators same.
- The rational number having the greater numerator is greater.
Consider two rational numbers \(\frac{p}{q}\) and \(\frac{r}{s}\).
We represent them on the number line. If they correspond to the same point on the line, then
\(\frac{p}{q}=\frac{r}{s}\)
However, if \(\frac{p}{q} \neq \frac{r}{s}\)
Then \(\frac{p}{q}\) lies either to the left of \(\frac{r}{s}\) or the to right of \(\frac{r}{s}\).
If \(\frac{p}{q}\) lies to the left of \(\frac{r}{s}\) then
\(\frac{p}{q}<\frac{r}{s}\)
If \(\frac{p}{q}\) lies to the right of \(\frac{r}{s}\) then
\(\frac{p}{q}>\frac{r}{s}\)
To compare two rational numbers \(\frac{p}{q}\) and \(\frac{r}{s}\), we replace \(\frac{p}{q}\) and \(\frac{r}{s}\) by equivalent rational numbers with same (positive) denominators [we may take the common denominator as the least common multiple (L.C.M.) of the denominators] and then compare them.
Another procedure to compare two rational numbers with unequal denominators is as follows:
1. Write the two numbers \(\frac{p}{q}\) and \(\frac{r}{s}\) the standard form in a line.
2. Below \(\frac{p}{q}\), write the integer s × p and below the number \(\frac{r}{s}\), write the integer q × r.
\(\frac{p}{q}\)
s × p
\(\frac{r}{s}\)
q × r
3. Compare the integers s x p and qxr.
If s × p<q × r, then \(\frac{p}{q}<\frac{r}{s}\)
To compare two negative rational numbers, we compare them ignoring their negative signs and then reverse the order.
For example; to compare – \(\frac{7}{5}\) and \(\frac{5}{3}\) we first compare \(\frac{7}{5}\) and \(\frac{5}{3}\), we get \(\frac{7}{2}\) < \(\frac{5}{3}\)
We thus have \(\frac{-7}{5}\) and \(\frac{-5}{3}\).
12. Rational numbers between two rational numbers : There are infinitely many rational numbers between any two given rational numbers. Suppose we wish (o find rational numbers between –\(\frac{3}{5}\) and –\(\frac{1}{3}\). First, we find equivalent rational numbers having a common denominator.
First, we find equivalent rational numbers having a common denominator.
Thus, we write ;
\(\frac{-3}{5}=\frac{-9}{15}\) and \(\frac{-1}{3}=\frac{-5}{15}\)
Now, we choose two integers between two numerators -9 and – 5 of the equivalent rational numbers. If we choose
– 8, -7 and -6, then rational numbers; \(\frac{-8}{15}, \frac{-7}{15}\) and \(\frac{-6}{15}\)

By using this method we can insert as many rational numbers as we want between two rational numbers ; we will find that the list is unending.
You can insert as many as rational numbers as you want. To insert ‘n’ rational numbers, between two rational numbers, we shall multiply both the numerator and the denominator of the given rational number by ‘n + 1
So, to find 4 rational numbers between two rational numbers \(\frac{2}{5}\) and \(\frac{4}{5}\), we shall multiply the numerators and denominators of both the rational numbers by 4 + 1 = 5.
Operations on Rational Numbers
In the previous class, we have learnt to add subtract, multiply and divide integers as well as fractions.
In this chapter, we shall extend the scope of these operations to rational numbers.
Addition of Rational Numbers
1. If \(\frac{p}{q}\) and \(\frac{r}{s}\) are two rational numbers (with same denominator q)
Then \(\frac{p}{q}+\frac{r}{q}=\frac{p+r}{q}\)
2. If \(\frac{p}{q}\) and \(\frac{r}{s}\) are two rational numbers then
\(\frac{p}{q}+\frac{r}{s}=\frac{p \times s+r \times q}{q \times s}\)
Remark: If the two denominators have a common factor, we may take the common denominator as the L.C.M. of he two denominators instead of their product.
![]()
Additive Inverse of a Rational Number
If x is a rational number then – x is a rational number such that x + (- x) = (- x) + x = 0 ; – x is called the additive inverse of x.
Also x is called the additive inverse of -x;
For example :
Additive inverse of \(\frac{6}{11}\) is \(\frac{-6}{11}\) and additive inverse of \(\frac{-6}{11}\) is \(\frac{6}{11}\)
Subtraction of Rational Numbers
While subtracting two rational numbers, we add the additive inverse of the rational number that is being subtracted to the other rational number.
If \(\frac{p}{q}\) and \(\frac{r}{s}\) are two rational numbers then

Multiplication of Rational Numbers
The product or multiplication of two rational numbers is just like the product of two fractions.
If \(\frac{p}{q}\) and \(\frac{r}{s}\) are two rational numbers then
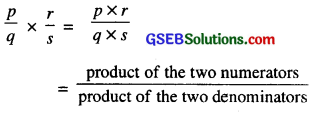
Reciprocal of a Rational Number
For any non-zero rational number \(\frac{p}{q}\) we have another non-zero rational number \(\frac{q}{p}\). This number \(\frac{q}{p}\) is called reciprocal of \(\frac{p}{q}\). Also
\(\frac{p}{q}\) is the reciprocal of \(\frac{q}{p}\). The number \(\frac{7}{3}\) is the reciprocal of \(\frac{3}{7}\).

Divison of Rational Numbers
To divide one rational number by the other non-zero rational number, we multiply the rational number by the reciprocal of the other.
If \(\frac{p}{q}\) and non-zero \(\frac{r}{s}\) are two rational numbers, then