This GSEB Class 7 Maths Notes Chapter 7 Congruence of Triangles covers all the important topics and concepts as mentioned in the chapter.
Congruence of Triangles Class 7 GSEB Notes
Congruent objects and congruence:
Two objects are congruent if they have same shape and size. The relation of two objects being congruent is called congruence. Keys of same lock, shaving blades of the same company, sheets of the same letter pad, biscuits in the same packet, toys made of the same mould, two stamps of the same denominations etc. are the examples of congruent objects.
Congruence: In our daily life we deal with many shapes and figures. We find that some of the shapes are exactly same to each other. Let us check whether the following figures have the same size and shape ?
1. These two squares are of different size but same shape.
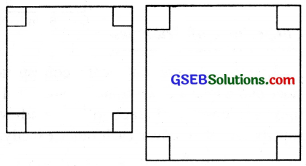
2. The two postal stamps have same size and same shape.

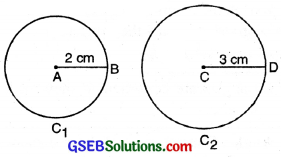
3. These two circles are of same shape but different size.
So, we observe that two postal stamps have same shape and same size. Therefore, they are congruent. In general, two objects are called congruent if and only if they have exactly the same shape and the same size. The relation of two objects being congruent is called ‘ ‘congruence’
Congruence of Plane Figures
The plane figures are compared using the method of superposition. If figure F1 is congruent to figure F2 we write F1 = F2
Congruence Among line Segments
If two line segments have same (i.e. equal) length, they are congruent.
Also, if two line segments are congruent, they have the same length.

Line segments are congruent ⇔ Their lengths are same
In fig., trace copy of CD completely covers AB
Hence \(\overline{\mathrm{AB}} \cong \overline{\mathrm{CD}}\)
Note: The symbol ⇔ is used to mean that the two statements given are such that, if one of them is given it means the other too.
Congruence of Angles
Two angles are congruent if they have the same measure.
Angles Congruent ⇔ Angles measures same
In the given fig., trace copy of ∠PQR completely covers ∠ ABC. So we write ∠ABC = ∠PQR which means ∠ABC = ∠PQR
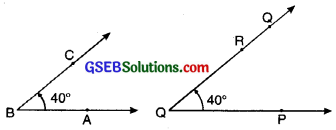
![]()
Congruence of Some More Plane Figures
1. Two circles are congruent, if they have equal radii. Conversely if raddi of Two circles are equal they are congruent. In figure Circle C1 ≅ Circle C2.
2. Two squares are congruent, if they have equal sides. Conversely, two congruent squares have equal sides. In the following figure square ABCD = square PQRS but
3. Two rectangles are congruent if they have equal length and breadth. Conversely two congruent rectangles have equal length and breadth. Here rectangle ABCD rectangle LMNO.
4. Two rectangles are congruent if they have equal length and breadth. Conversely two congruent rectangles have equal length and breadth. Here rectangle ABCD rectangle LMNO.
Congruence of Triangles
Two triangles are congruent if corresponding sides and angles of two triangles are equal and they are copies of each other, and when superposed, they cover each other exactly.
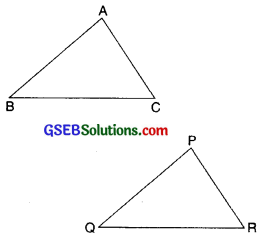
∆ABC and ∆PQR have the same size and shape. They are congment. So we would express this as
∆ABC ≅ ∆PQR.
This means that, when you place ∆PQR on ∆ABC, P falls on A, Q falls on B and R falls on C, also \(\overline{\mathrm{PQ}}\) falls along \(\overline{\mathrm{AE}}\), \(\overline{\mathrm{QR}}\) falls along \(\overline{\mathrm{BC}}\) and \(\overline{\mathrm{PR}}\) falls along AC
It follow immediately that
AB = PQ, BC = QR and AC = PR
∠A = ∠P, ∠B = ∠Q and ∠C = ∠R
i. e. the matching parts (corresponding parts) of congruent triangles are equal.
If you place ∆PQR on ∆ABC such that P falls on B, then, should the other vertices also correspond suitably? It need not happen! Take trace copies of the triangles and try to find out This shows that while talking about congruence of triangles, not only the measures of angles and lengths of sides matter, but also the matching of vertices. In the above case, the correspondence is
A ↔ P, B ↔ Q, C ↔ R
We may write this as
ABC ↔ PQR
Note. The corresponding parts of congruent triangle are always equal. In short, it is written as (c.p.c.t.) (corresponding parts of congruent triangles)
Criteria for congruence of triangles
If we have two triangles drawn in own notebook and want to verify if they are congruent, we cannot everytime cut out one of them and use method of superposition.
Everytime all the six elements (i.e. three sides and three angles) are not necessarily required to be verified for establishing the congruence of two triangles. When some of the conditions hold good the others, are found to be true automatically. Let us construct two triangles with the same measure and try to establish congruence criterion one by one.
I. SSS Congruence Criterion.
SSS stands for side-side-side. If under a given correspondence, the three sides of the triangle are respectively equal to the three sides of another triangle, then the two triangles are congruent.
In the following fig.,
We find that
AB = DE, BC = EF and CA = FD
So by SSS criterion of congruence We find that
∆ABC ≅ ∆DEF

II. SAS Congruence criterion
SAS stands for side-angle-side. SAS criterion states that two triangles are congruent if two sides and the angle- between them of one triangle are equal to the corresponding sides and angle of the other triangle.
In the following fig., we find that
AB = DE
∠A = ∠D
and AC = DF
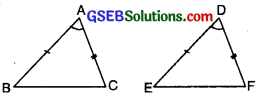
So, by SAS criterion of congruence we find that ∆ABC ≅ ∆DEF.
![]()
III. ASA Congruence Criterion.
ASA stands for Angle-Side-Angle. ASA criterion states that two triangles are congruent if two angles and side between two angles of one triangle are respectively equal to the two angles and side between two angles of the other triangle.
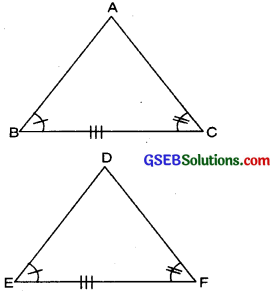
∠B = ∠E
∠C = ∠F and BC = EF
So by ASA Criterion of Congruence, we find that ∆ABC ≅ ∆DEF.
IV. RHS Congruence Criterion.
RHS stands for right angle, hypotenuse, side, RHS criterion states that two right angled triangles are congruent, if the hypotenuse and one side of the first triangle are equal to the hypotenuse and one side of the second triangle.