This GSEB Class 7 Maths Notes Chapter 8 Comparing Quantities covers all the important topics and concepts as mentioned in the chapter.
Comparing Quantities Class 7 GSEB Notes
In our daily life, there are many occations when we compare two quantities. They may be heights, weights, salaries, marks etc.
To do this, we should be well versed in concepts that involve comparisons such as ratios, proportions and percentages. Thus, to broaden our horizons as a banker or an economist, we need to possess a strong and indepth knowledge and understanding of mathematics.
Mathematics helps us to be a logical thinker.
1. Ratio: When we compare two quantities of same kind by division, we say that we have formed a ratio of the two quantities. The ratio of two quantities of the same kind and in the same unit is the fraction that one quantity is of the other.
Usually we use symbol to express a ratio.
We can say that the ratio of the weight of Anuj to that Sunil is 15:45; read as 15 is to 45.
In general; for any non-zero numbers a and b, a is to b is a ratio \(\frac{a}{b}\). written as a:b. b
Thus it is clear that ratio can be expressed as a fraction.
2. Ratio in the simplest form:
- A ratio a: b is said to be in the simplest form if its antecedent a and consequent b have no common factor except 1.
- A ratio in the simplest form is also called the ratio in the lowest terms.
3. Equivalent Ratios:
- As we know that the fraction does not change when its numerator and denominator are multiplied or divided by the same non-zero number.
- So, a ratio does not alter, if its first and second term are multiplied or divided by the same non-zero number.
4. Comparison of Ratios:
Steps of comparing ratios are as follows:
- Write each of the ratios in the form of respective fraction in the simplest form,
- Find the L.C.M. of denominators of two fractions.
- Make each of the fractions its respective equivalent fractions in such a way that the denominators of each of the equivalent fractions should be equal to L.C.M. found in step (2).
- Compare the numerators of each of the equivalent fractions. The fraction having larger numerator will be larger than the other.
5. Proportion: The ratios which are equivalent are said to be in proportion. Four numbers a, b, c, d are in proportion.

In proportion; Product of means = Product of extremes
6. Use of proportion in solving problems: Before you start solving a problem using proportion, you need to determine whether the type of proportion is direct or indirect. Let us analyse some problems to identify the type of proportion and solve them.
![]()
Proportion can be direct or indirect
Direct Proportion: The given quantities are said to be in direct proportion if with increase or decrease in one quantity leads to increase or decrease respectively in the other quantity.
Indirect Proportion: The given quantities are said to be in indirect proportion if with increase in one quantity the other quantity decreases and vice versa.
Meaning of Percentage
Percentage is derived from Latin word ‘per centum’ meaning ‘per hundred’. Percentage is represented by the symbol % and means hundredths too. That is 1% means it is 1 out of hundred which can be written as:
1% = \(\frac{1}{100}\) = 0.01.
Also, Percentages are numerators of fractions with denominator 100 and have been used in comparing results.
Conversion of Percentage into a Fraction.
Rule:
- Obtain the given per cent. Let it be x%.
- Drop the percent sign (i.e. %) and divide the number by 100 and simplify.
Thus x% = \(\frac{x}{100}\)
Conversion of a Fraction into Percentage
Rule:
- Let fraction be \(\frac{a}{b}\).
- Multiply the fraction by 100 and put the percent sign % to obtain the required percent.
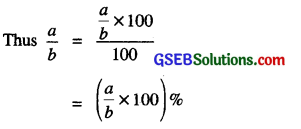
Conversion of Decimal Into a Percentage
Rule:
To convert decimal into percent, shift the decimal point two places to right and write % sign.
Conversion of Percentage into Decimal
Rule:
- Write the percent which is to be converted into a decimal.
- Express the given percent as a fraction with denominator as 100.
- Now write the fraction obtained in step 2 in decimal form.
Conversion of Ratio into Percentage
Rule:
- Write the ratio; Let it be a: b.
- Convert the given ratio into the fraction \(\frac{a}{b}\)
- Multiply the fraction as obtained as in step 2 by 100 and put percent sign %.
Conversion of Percentage into a Ratio
Rule:
- Write the given percent.
- Convert the given per cent into a fraction by dividing it by 100 and removing percent sign; %.
- Express the fraction obtained in step 2 in the simplest (or lowest) form.
- Express the fraction obtained in step 3 as a ratio.
Finding the Percentage of a given Quantity.
Rule:
- Write the quantity; say „v.
- Write the required percent; say P%.
- Multiply x by P and divide by 100 to obtain the required P% of x.
i.e. P% of x = \(\frac{P}{100}\) × 100
![]()
Ratios to Percents
Some time parts are given to us in the form of ratios and we need to convert those to percentages.
Rule:
Let given number be N.
We wish to divide it in two parts in the given ratio, say a: b
Therefore
First part of N = \(\frac{a}{a+b}\) × N
In percentage ; first part = \(\frac{a}{a+b}\) × 100%
Second part of N = \(\frac{b}{a+b}\) × N a + b
In percentage ; second part
= \(\frac{b}{a+b}\) × 100%
Increase or Decrease as Percentage
There are many times when we need to know. What the increase in a certain quantity or decrease in it as per cent. We convert the increase or decrease as a percentage of the initial amount.
Thus percentage increase
(\(\frac{\text { Increased quantity }}{\text { Original quantity }}\) × 100) %
Percentage decrease
= (\(=\left(\frac{\text { Decreased quantity }}{\text { Original quantity }}\) × 100)%
Profit or Loss as Percentage
Profit and loss percentage is always calculated on the cost price.
- Profit percentage = (\(\frac{\text { Profit }}{\text { CP }}\) × 100)%
- Loss percentage = (\(\frac{\text { Loss }}{\text { CP }}\) × 100)%
Simple Interest
Interest. When we borrow money from a bank or a money lender, w need to pay the money back after a period along with some extra money. This extra money is called the Interest. The amount of interest we pay depends on: Principal. The money we borrow, called the Principal (P).
Rate. The rate of interest per annum, R (in percent).
Time. The time for which the money is borrowed, T (in years)
Simple Interest = \(\frac{\text { Principal } \times \text { Rate } \times \text { Time }}{100}\)
i.e I = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
Note: Given any three quantities out of P, R, T and I;
We can claculate he fourth quantity by using the above formula.
Amount. The total money paid by the borrower to the money lender is called mount Thus, Amount = Principal + Interest If P denotes the principal, I is interest paid and A the amount, then
A = P + I