This GSEB Class 9 Maths Notes Chapter 11 Circles covers all the important topics and concepts as mentioned in the chapter.
Circles Class 9 GSEB Notes
To draw precise figures, one must have a geometry box that contains the following:
- A graduated scale: On one side of the graduated scale centimetres and millimetres are marked off and on the. other side inches and their parts are marked off.
- A pair of set-squares: One set-square with angles 90°, 60° and 30° and other set-square with angles 90°, 45° and 45°.
- A pair of dividers (or a divides): A divider has two pointed ends which can be adjusted to compare different lengths.
- A pair of compasses (or a compass): A compass has provision of fitting a pencil at one end to draw desired circle.
- A protractor
The process of drawing a geometrical figure using only two instruments – an ungraduated ruler (straight edge) and a compass is called geometrical construction. In construction where measurements are also required a graduated scale as well as a protractor can be used.
In the first part of these chapter, we will study some basic constructions as listed below. We will use only a straight edge and a compass for these constructions.
- Construction of the bisector of a given angle.
- Construction of the perpendicular bisector of a given line segment.
- Construction of an angle of measure 60°.
- Construction of angles with measures in multiples of 15°.
We will also justify the validity of certain constructions.
Example 1:
To construct the bisector of a given angle.
Answer:
Given an angle ABC, we want to construct its bisector.
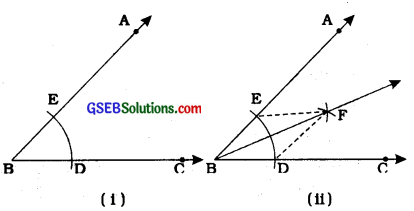
Steps of construction:
- Taking B as centre and any radius, draw an arc to intersect the rays BA and BC, say at E and D respectively [see figure (i )]
- Taking D and E as centres and with the radius more than DE, draw arcs to intersect each other, say at E
- Draw the ray BF [see figure (ii)].
This ray BF is the required bisector of the angle ABC.
Justification:
Join DF and EF.
In A BEF and A BDF,
BE = BD {Radii of the same arc)
EF = DF (Arcs of equal radii)
BF = BF (Common)
∴ ∆BEF = ∆BDF (SSS rule)
∴ ∠ EBF = ∠DBF (CPCT)
∴ ∠ ABF = ∠ CBF
Example 2:
To construct the perpendicular bisector of a given line segment.
Answer:
Given a line segment AB, we want to construct , its perpendicular bisector.
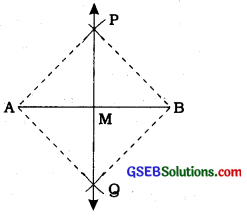
Steps of construction:
- Taking A and B as centres and radius more than AB, draw arcs on both sides of the line segment AB (to intersect each other).
- Let these arcs intersect each other at P and Q. Join PQ (see figure).
- Let PQ intersect AB at the point M. Then line PMQ is the required perpendicular bisector of AB.
Justification:
Join A and B to both P and Q to form AR AQ, BP and BQ.
In ∆PAQ and ∆PBQ,
AP = BP (Arcs of equal radii)
AQ = BQ (Arcs of equal radii)
PQ = PQ (Common)
∴ ∆PAQ ≅ ∆PBQ (SSS rule)
∴ ∠APQ = ∠BPQ (CPCT)
∴ ∠APM = ∠BPM
Now in ∆PMA and ∆PMB,
AP = BP (As before)
PM = PM (Common)
∠APM = ∠BPM (Proved above)
∴ ∆PMA ≅ ∆PMB (SAS rule)
∴ AM = BM and ∠PMA = ∠PMB (CPCT)
But, ∠PMA + ∠PMB = 180° (Linear pair)
∴ ∠PMA = ∠PMB = \(\frac{180^{\circ}}{2}\) = 90°.
Therefore, PM, that is, PMQ is the perpendicular bisector of AB.
![]()
Example 3:
To construct an angle of 60° at the initial point of a given ray.
Answer:
Let us take a ray AB with initial point A [see figure (i)]. We want to construct a ray AC such that ∠CAB = 60°.
Steps of construction:
1. Taking A as centre and some radius, draw an arc of a circle, which intersects AB, say at a point D.
![]()
2. Taking D as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point E.
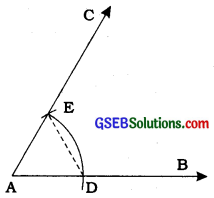
3. Draw the ray AC passing through E [see figure (ii)].
Then ∠CAB is the required angle of 60°.
Justification:
Join DE.
Then, AE = AD = DE (By construction)
Therefore, ∆EAD is an equilateral triangle and the ∠EAD, which is the same as ∠CAB is equal to 60°.
Some constructions of triangles:
According to the rules of congruence viz. SAS, SSS, ASA (or AAS) and RHS rules if-
- two sides and the included angle is given,
- three sides are given,
- two angles and the included side (or anyone side) is given
- in a right triangle, the hypotenuse and one side is given, a unique triangle can be constructed.
Now, we will study some more constructions of triangle as mentioned below:
- Construction of a triangle, given its base, a base angle and the sum of other two sides.
- Construction of a triangle, given its base, a base angle and the difference of other two sides.
- Construction of a triangle, given its perimeter and its two base angles.
Example 1:
Construction 11.4:
To construct a triangle, given its base, a base angle and sum of other two sides.
Answer:
Given the base BC, a base angle, say ∠B and the sum AB + AC of the other two sides of a triangle ABC, you are required to construct
it.
Steps of construction:
- Draw the base BC and at the point B make an angle, say XBC equal to the given angle.
- Cut a line segment BD equal to AB + AC from the ray BX.
- Join DC and make an angle DCY equal to ∠BDC.
- Let CY intersect BX at A (see the figure).
Then, ABC is the required triangle.
Justification:
Base BC and Z B are drawn sis given.
Next in AACD,
∠ACD = ∠ADC (By construction)
∴ AC = AD
Then, AB = BD – AD = BD – AC
∴ AB + AC = BD
Alternative method:
Follow the first two steps as above. Then draw perpendicular bisector PQ of CD to intersect BD at a point A (see the figure). Join AC. Then, ABC is the required triangle.
Note that A lies on the perpendicular bisector of CD, therefore AD = AC.

Remark: The construction of the triangle is not possible if the stun AB + AC = BC.
Example 2:
To construct a triangle given its base, a base angle and the difference of the other two sides.
Answer:
Given the base BC, a base angle, say Z B and the difference of other two sides AB – AC or AC – AB, you have to construct the triangle ABC.
Clearly there are following two cases:
Case 1: Let AB > AC, that is, AB – AC is given.
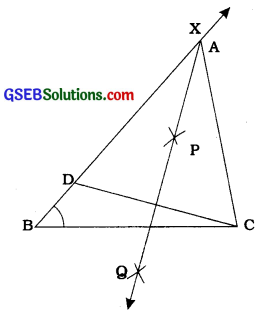
Steps of construction:
- Draw the base BC and at point B make an angle say XBC equal to the given angle.
- Cut the line segment BD equal to AB – AC from ray BX.
- Join DC and draw the perpendicular bisector, say PQ of DC.
- Let PQ intersect BX at a point A. Join < AC (see the figure).
Then, ABC is the required triangle.
Justification:
Base BC and ∠B are drawn as given. The point A lies on the perpendicular bisector of DC.
∴ AD = AC
BD = AB – AD = AB – AC
Case 2: Let AB < AC, that is, AC – AB is given.
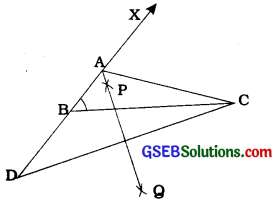
Steps of construction:
- Same as in case 1.
- Cut line segment BD equal to AC – AB from the line BX extended on opposite; side of line segment BC.
- Join DC and draw the perpendicular bisector, say PQ of DC.
- Let PQ intersect BX at A. Join AC (see the figure).
Then, ABC is the required triangle.
We can justify the construction as in case 1.
Example 3:
Construction 11.6:
To construct a triangle, given its perimeter and its two base angles.
Answer:
Given the base angles, say Z B and Z C and BC + CA + AB, you have to construct the triangle ABC.
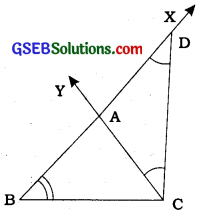
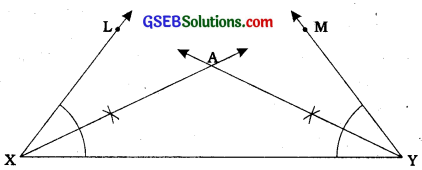
Steps of construction :
- Draw a line segment, say XY equal to BC + CA + AB.
- Make angles LXY equal to ∠B and MYX equal to ∠C.
- Bisect ∠LXY and ∠MYX. Let these bisectors intersect at a point A [see figure]
- Draw perpendicular bisectors PQ of AX and RS of AY.
- Let PQ intersect XY at B and RS intersect XY at C. Join AB and AC [see figure].
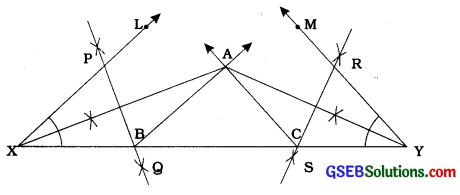
Justification:
B lies on the perpendicular bisector PQ of AX.
Therefore, XB = AB and similarly, CY = AC.
This gives, BC + CA + AB = BC + CY + XB = XY.
Again, ∠BAX = ∠AXB (As in ∆AXB, AB = XB) and ∠ABC = ∠BAX + ∠AXB = 2∠AXB = ∠LXY ,
Similarly, ∠ACB = ∠MYX as required.
![]()
Example 4:
Construct a triangle ABC, in which ∠B = 60°, ∠C = 45° and AB + BC + CA = 11 cm.
Answer:
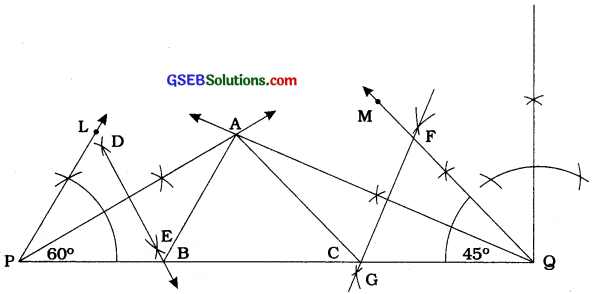
Steps of construction:
- Draw a line segment PQ =11 cm. (PQ = AB + BC + CA).
- At P construct an angle of 60° and at Q, an angle of 45°.
- Bisect these angles. Let the bisectors of these angles intersect at a point A.
- Draw AP and AQ. Draw perpendicular bisectors DE of AP to intersect PQ at B and FG of AQ to intersect PQ at C.
- Join AB and AC (see the figure).
Then, ABC is the required triangle.