This GSEB Class 9 Maths Notes Chapter 12 Surface Areas and Volumes covers all the important topics and concepts as mentioned in the chapter.
Surface Areas and Volumes Class 9 GSEB Notes
Area of a triangle:
We are familiar with the following formula used to find the area of a triangle which is applicable to all the types of triangle:
Area of a triangle = \(\frac{1}{2}\) × base × height
For some particular types of triangle, the same formula can be represented in other forms.
For a right-angled triangle, the formula can be taken as below:
Area of a right triangle = \(\frac{1}{2}\) × product of the sides forming the right angle
- In case of an equilateral triangle, its height can be found using Pythagoras’ theorem. In that case the formula will be changed as below:
Area of an equilateral triangle = \(\frac{\sqrt{3}}{4}\) × (side)2 - In case of an isosceles triangle, if all the sides are known, the height corresponding to the base can be found using Pythagoras’ theorem and the original formula can be , used.
- But in case of a scalene triangle, the height cannot be found even if all the three sides are known.
Heron’s formula:
For any type of triangle, if all the sides are known, its area can be calculated by the following formula given by mathematician Heron:
Area of a triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\)
Here, a, b and c denote the length of three sides of the triangle and s = \(\frac{a+b+c}{2}\) is the semi perimeter of the triangle.
Units of area:
Area of small planar figures are usually denoted using units square metre (m2) or square centimetre (cm2), etc. The area of plots of land are usually denoted in hectares. 1 hectare = 10,000 m2
An important result: if the sides of a triangle measure 2n2 + 1, 2n2 + 2 and 4n2 + 1, where n is a natural number, its semiperimeter s will be 4n2 + 2 and its area will be 2n(2n2 + 1) = n × s. Here, area will be given by a natural number always, not an irrational number. There can be other forms also.
Example 1:
Find the area of a triangle, two sides of which are 8 cm and 11 cm and the perimeter is 32 cm (see the given figure).

Answer:
Here, the perimeter of the triangle = 32 cm. a = 8 cm and b = 11 cm.
∴ Third side c = 32 cm – (8 + 11) cm = 13 cm
Here, 2s = 32, i.e., s = 16cm,
s – a = (16 – 8) cm = 8 cm,
s – b = (16 – 11)cm = 5cm and
s – c = (16 – 13) cm = 3 cm.
Now, area of the triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{16 \times 8 \times 5 \times 3}\) cm2
= 8√30 cm2
![]()
Example 2:
A triangular park ABC has sides 120 m, 80 m and 50 m (see the given figure). A gardener Dhania has to put a fence all around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate of ₹ 20 per metre leaving a space 3 m wide for a gate on one side.
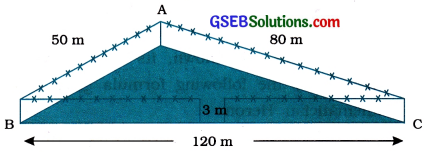
Answer:
For finding area of the park, we have 2s = 50m + 80m + 120 m = 250 m s = 125 m
Now, s – a = (125 – 120) m = 5 m,
s – b = (125 – 80) m = 45 m and
s – c = (125 – 50) m = 75 m.
Area of the park = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{125 \times 5 \times 45 \times 75}\) m2
= 375√15 m2
Also. perimeter of the park = AB + BC + CA
= 250m
Then, length of the wire needed for fencing
= 250 m – 3 m (to be left for gate)
= 247 m
So, the cost of fencing = ₹ 20 × 247 = ₹ 4940
Example 3:
The sides of a triangular plot are in the ratio of 3:5:7 and its perimeter is 300 m. Find its area.
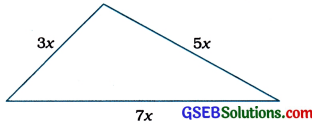
Answer:
Suppose that the sides, in metres, are 3x, 5x and 7x (see the given figure).
Then, 3x + 5x + 7x = 300 (perimeter of the triangle)
∴ 15x = 300
∴ x = 20.
So the sides of the triangle are 3 × 20 m, 5 × 20 m and 7 × 20 m, i.e., 60 m, 100 m and 140 m.
Here, s = \(\frac{60+100+140}{2}\)m = 150 m
∴ Area of the plot
= \(\sqrt{150(150-60)(150-100)(150-140)}\)m2
= \(\sqrt{150 \times 90 \times 50 \times 10}\) m2
= 1500√3 m2
Application of Heron’s formula in finding areas of quadrilaterals :
In a quadrilateral, if the measures of four sides and one diagonal / is given, its area can be found by finding the areas of two triangles formed by the diagonal with the help of Heron’s formula.
In quadrilateral ABCD, if h1 and h2 are the lenghts of altitudes drawn from B and D respectively to AC, then
Area of quadrilateral ABCD = Area of ∆ ABC + Area of ∆ ACD
= (\(\frac{1}{2}\) × AC × h1) + (\(\frac{1}{2}\) × AC × h2
= \(\frac{1}{2}\) × AC × (h1 + h2)
We do have the formule for the area of some special quadrilaterals as:
Area of a square = (length)2 = \(\frac{(\text { diagonal })^{2}}{2}\)
Area of a rectangle = length × breadth
Area of a parallelogram = base × corresponding altitude
Area of a rhombus = \(\frac{1}{2}\) × product of two diagonals
Area of a trapezium = \(\frac{1}{2}\) × stun of parallel sides × distance between parallel sides
Example 1:
Kamla has a triangular field with sides 240 m, 200 m, 360 m, where she grew wheat. In another triangular field with sides 240 m, 320 m, 400 m adjacent to the previous field, she wanted to grow potatoes and onions (see the given figure). She divided the field in two parts by joining the midpoint of the longest side to the opposite vertex and grew potatoes in one part and onions in the other part. How much area (in hectares) has been used for wheat, potatoes and onions? (1 hectare = 10000 m )
Answer:
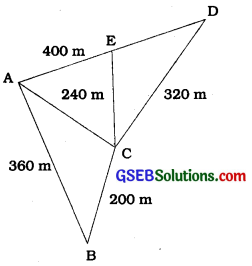
Let, ABC be the field where wheat is grown.
Also let ACD be the field which has been divided in two parts by joining C to the midpoint E of AD.
For the area of triangle ABC, we have
a = 200 m, b = 240 m, c = 360 m
∴ s = \(\frac{200+240+360}{2}\) m = 400 m
So, area for growing wheat
= \(\sqrt{400(400-200)(400-240)(400-360)}\)m2
= \(\sqrt{400 \times 200 \times 160 \times 40}\) m2
= 16000 √2 m2 = 1.6 × √2 hectares
= 2.26 hectares (nearly)
Let us now calculate the area of triangle ACD.
Here, we have s = \(\frac{240+320+400}{2}\)m = 480 m
So, area of ∆ACD
= \(\sqrt{480(480-240)(480-320)(480-400)}\)m2
= \(\sqrt{480 \times 240 \times 160 \times 80}\)m2
= 38400 m2 = 3.84 hectares
We notice that the line segment joining the b midpoint E of AD to C divides the triangle AGD in two parts equal in area.
Therefore, area for growing potatoes
= area for growing onions
= (3.84 + 2) hectares = 1.92 hectares
Example 2:
Students of a school staged a rally for \ cleanliness campaign. They walked through ; the lanes in two groups. One group walked
through the lanes AB, BC and CA; while the other through AC, CD and DA (see the given figure). Then they cleaned the area \ enclosed within their lanes. If AB = 9 m, BC = 40 m, CD = 15 m, DA = 28 m and ∠B = 90°, which group cleaned more area and by how much ? Find the total area cleaned by the students (neglecting the width of the lanes).
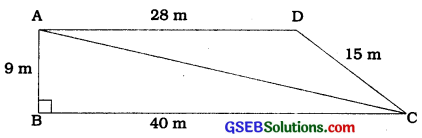
Answer:
In ∆ABC, ∠B = 90°; AB = 9 m and BC = 40 m.
Then, AC = \(\sqrt{9^{2}+40^{2}}\) m
= \(\sqrt{81+1600}\) m
= √1681 m = 41 m
Therefore, the first group has to clean the area of triangle ABC, which is right angled. Area of ∆ ABC = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 40 × 9 m2 = 180 m2
The second group has to clean the area of triangle ACD, which is scalene having sides 41m, 15 m and 28 m.
Here, s = \(\frac{41+15+28}{2}\)m = 42 m
Then, area of ∆ACD
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{42(42-41)(42-15)(42-28)}\) m2
= \(\sqrt{42 \times 1 \times 27 \times 14}\) m2 = 126 m2
So, first group cleaned 180 m2 which is (180 – 126) m2, i.e., 54 m2 more than the area cleaned by the second group.
Total area cleaned by all the students = (180 + 126) m2 = 306 m2.
![]()
Example 3:
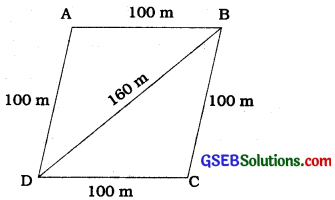
Sanya has a piece of land which is in the shape of a rhombus (see the given figure). She wants her one daughter and one son to work on the land and produce different crops. She divided the land in two equal parts. If the perimeter of the land is 400 m and one of the diagonals is 160 m, how much area each of them will get for their crops?
Answer:
Let, ABCD be the field.
Perimeter = 400 m
So, each side = 400 m ÷ 4 = 100 m
i.e., AB = AD = 100 m
Let, diagonal BD=160m
Then, semiperimeter s of ∆ABD is given by
s = \(\frac{100+100+160}{2}\) m = 180 m
Hence, area of ∆ABD
= \(\sqrt{180(180-100)(180-100)(180-160)}\) m2
= \(\sqrt{180 \times 80 \times 80 \times 20}\) m2
= 4800 m2
Therefore, each of them will get an area of 4800 m2.
Alternative method:
Draw CE ⊥ BD (see the given figure).
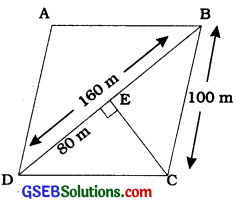
As BD = 160 m, we have
DE = 160 m2 = 80 m
Now, DE2 + CE2 = DC2
CE = \(\sqrt{\mathrm{DC}^{2}-\mathrm{DE}^{2}}\)
CE = \(\sqrt{100^{2}-80^{2}}\) m = 60 m
Therefore, area of ∆BCD = \(\frac{1}{2}\) × 160 × 60 m2
= 4800 m2