This GSEB Class 9 Maths Notes Chapter 13 Surface Areas and Volumes covers all the important topics and concepts as mentioned in the chapter.
Surface Areas and Volumes Class 9 GSEB Notes
Surface area of a cuboid and a cube:
When we cut out many rectangles of the same shape and size from cardboard and stack them up in a verticle pile, we get a cuboid. Cuboid is a solid shape having six rectangular surfaces. Sometimes, one pair of opposite surfaces of a cuboid may be square.
Total surface area of a cuboid = 2 (lb + bh + hl); where l, b and h are three edges of the cuboid. In other words, l; b and h are the length, breadth and height respectively of the cuboid.
- A cuboid, in which length, breadth and height are all equal, is called a cube.
- Total surface area of a cube = 6a2, where a is the edge (or length) of the cube.
- In a cuboid and a cube, the surfaces other than the bottom and the top are called lateral surfaces.
- Lateral surface area of a cuboid = 2h (l + b) = height × perimeter of base
- Lateral surface area of a cube = 4a2
- 1 m2 = 10,000cm2
- 1 hectare = 10,000 m2
Example 1:
Mary wants to decorate her Christmas tree. She wants to place the tree on a wooden box covered with coloured paper with picture of Santa Claus on it (see the given figure). She must know the exact quantity of paper to buy for this purpose. If the box has length, breadth and height as 80 cm; 40 cm and 20 cm respectively, how many square sheets of paper of side 40 cm would she require?

Answer:
Since Mary wants to paste the paper on the outer surface of the box; the quantity of paper required would be equal to the surface area of the box which is of the shape of a cuboid.
The dimensions of the box are:
Length = 80 cm,
Breadth = 40 cm and
Height = 20 cm.
The total surface area of the box = 2 (lb + bh + hl)
= 2 [(80 × 40) + (40 × 20) + (20 × 80)] cm2
= 2 [3200 + 800 + 1600] cm2
= 2 × 5600 cm2 = 11200 cm2
The area of each sheet of the paper = 40 × 40 cm2
= 1600 cm2
Then, the number of sheets required total surface area of box
= \(\frac{\text { total surface area of box }}{\text { area of one sheet of paper }}\)
= \(\frac{11200}{1600}\) = 7
Thus, she would require 7 sheets.
Note: Here, the number of sheets required for areas 2lb, 2bh and 2hl are 4, 1 and 2 respectively. As all the measures of the box are not multiples of the measures of the sheet, she will need to cut one sheet of paper (for bh region) into two equal parts.
![]()
Example 2:
Hameed has built a cubical water tank with lid for his house, with each outer edge 1.5 m long. He gets the outer surface of the tank excluding the base, covered with square tiles of side 25 cm (see the given figure). Find how much he would spend for the tiles, if the cost of the tiles is ₹ 360 per dozen.

Answer:
Since Hameed is getting the five outer faces of the tank covered with tiles, he would need to know the surface area of the tank excluding the area of the base, to decide on the number of tiles required.
Edge of the cubical tank = 1.5 m = 150 cm (= a)
So, surface area of the tank to be covered with tiles = 5 × 150 × 150 cm2.
Area of each square tile = side × side
= 25 × 25 cm2
So, the number of tiles required

= 5 × 6 × 6 =180
Cost of 1 dozen tiles, i.e., cost of 12 tiles = ₹ 360
Therefore, cost of one tile = ₹ \(\frac{360}{12}\) = ₹ 30
So, the cost of 180 tiles = 180 x ₹ 30 = ₹ 5400
Note: In the problems related to areas of breakable items, while taking the quotient of two areas, the division should be taken measure by measure like \(\left(\frac{150}{25}\right)\) as shown in the above example. If it does not yield integers, it suggest that the items (tiles here) are required to be broken.
Surface area of a right circular cylinder:
When we cut out many circles of the same size from cardboard and stack them vertically up, we get a right circular cylinder. If the shape cut out from cardboard is not circle or if they are not stacked vertically, then we do not get right circular cylinder. We will be dealing with right circular cylinders only. So, unless stated otherwise, the word cylinder would mean a right circular cylinder.
A cylinder has a curved surface and two plane circular surfaces one at the base and the other at the top. The radii of the base and the top are always equal. The radius of the base is also called the radius of the cylinder. So, unless stated otherwise, radius of a cylinder shall mean base radius of the cylinder.
Curved surface area of a cylinder = 2 πrh
Here, r = radius of the cylinder and
h = height of the cylinder Curved surface area of a cylinder = πdh.
Here, d = diameter of the cylinder = 2r
- Curved surface area of a cylinder = Circumference of base × height
- Total surface area of a cylinder = 2πr (r + h]
- π is an irrational number. So, its decimal expansion is non-terminating non-recurring. But, for calculation purpose, we will use its approximate value \(\frac{22}{7}\) or 3.14.
Example 1:
Savitri had to make a model of a cylindrical kaleidoscope for her science project. She wanted to use chart paper to make the curved surface of the kaleidoscope, (see the given figure). What would be the area of chart paper required by her, if she wanted to make a kaleidoscope of length 25 cm with a 3.5 cm radius? You may take π = \(\frac{22}{7}\)

Answer:
Radius of the base of the cylindrical kaleidoscope (r) = 3.5 cm.
Height (length) of kaleidoscope (h) = 25 cm.
Area of chart paper required = curved surface area of the kaleidoscope
= 2πrh
=2 × \(\frac{22}{7}\) × 3.5 × 25 cm2
= 550 cm2
Surface area of a sphere and hemisphere:
Sphere:
when a circle is rotated around one of its diameter as axis, the shape obtained in space is called a sphere. The radius of the rotated circle is the radius of the sphere and the centre of the rotated circle is the centre of the sphere. A sphere has only one surface with is curved in nature. In other words, a sphere is a three dimensional figure (solid figure), which is made up of all points in the space, which he at a constant distance called the radius, from a fixed point called the centre of the sphere.
A cone has two surfaces :
One is Its curved surface and the other is the plane surface of its circular base.
There are three measures In a cone:
- Radius of the base or radius of cone r,
- HeIght h and
- Slant heIght 1.
These three measures are the measures of a right triangle and hence the relatIon l2 = r2 + h2 holds good always.
- Curved surface area of a cone = πrl
- total surface area of a cone = πrl + πr2
= πr(l + r) - For any cone, l2 = r2 + h2
Example 1:
Find the curved surface area of a right circular cone whose slant height is 10 cm and base radius is 7 cm.
Answer:
For the given cone, radius r = 7 cm and slant height l = 10cm.
Curved surface area of a cone
= πrl
= \(\frac{22}{7}\) × 7 × 10cm
= 220 cm2
Example 2:
The height of a cone is 16 cm and Its base radius Is 12 cm. Find the curved surface area and the total surface area of the cone. (Use π = 3.14).
Answer:
Here, height h = 16 cm and radius r = 12 cm.
So, from l2 = h2 + r2, we have
= \(\sqrt{16^{2}+12^{2}}\) cm
= 20 cm
Then, curved surface area of a cone = πrl
= 3.14 × 12 × 20 cm2
= 753.6 cm2
And, total surface area of a cone
= πrl + πr2
=(753.6 + 3.14 × 12 × 12)cm2
= (753.6 + 452.16) cm2
= 1205.76 cm2
Example 3:
A corn cob (see the given figure). shaped somewhat like a cone, has the radius of its broadest end as 2.1 cm and length (height) as 20 cm. If each 1 cm2 of the surface of the cob carries an average of four grains, find how many grains you would find on the entire cob.

Answer:
Since the grains of corn are found only on the curved surface of the corn cob, we would need to know the curved surface area of the corn cob to find the total number of grains on it. Here, radius r = 2.1 cm and height h 20 cm.
Now, l = \(\sqrt{r^{2}+h^{2}}=\sqrt{(2.1)^{2}+20^{2}}\) cm
= \(\sqrt{404.41}\) cm = 20.11cm
Then, the curved surface area of the corn
cob = πrl
= \(\frac{22}{7}\) × 2.1 × 20.11 cm2
= 132.726 cm2
= 132.73 cm2 (approx.)
Number of grains of corn on 1 cm2 of the surface of the corn cob = 4
Therefore, number of grains on the entire
curved surface of the cob = 132.73 × 4
= 530.92
= 531 (approx.)
Thus, there would be approximately 531 grains of corn on the cob.
Surface area of a sphere and hemisphere:
Sphere:
When a circle Is rotated around one of Its diameter as axis, the shape obtained in space Is called a sphere. The radius of the rotated circle Is the radius of the sphere and the centre of the rotated circle Is the centre of the sphere. A sphere has only one surface with Is curved In nature. In other words, a sphere is a three dimensional figure (solid figure), whIch is made up of all points in the space, which lie at a constant distance called the radius, from a fixed point called the centre of the sphere.
![]()
Hemisphere:
Dividing a sphere into two equal parts by a plane that passes through its centre, we get two hemispheres. A hemisphere has two surfaces – one is a curved surface and the other is a flat circular surface also called the base of the hemisphere.
- Surface area of a sphere = 4πr2, where r is the radius of the sphere.
- Curved surface area of a hemisphere = 2πr2, where ris the radius of the hemisphere.
- Total surface area of a hemisphere = 3πr2, where r is the radius of the hemisphere.
Example 1:
Find the surface area of a sphere of radius 7 cm.
Answer:
For the given sphere, radius r = 7 cm,
Surface area of a sphere
= 4 πr2 = 4 × \(\frac{22}{7}\) × 7 × 7 cur = 616 cm2
Example 2:
Find :
(i) the curved surface area and
Answer:
For the given hemisphere, radius r = 21 cm.
Curved surface area of a hemisphere
= 2 πr2 = 2 × \(\frac{22}{7}\) × 21 × 21 cm2
= 2772 cm2
(ii) the total surface area of a hemisphere of radius 21 cm.
Answer:
Total surface area of a hemisphere
3πr2 = 3 × \(\frac{22}{7}\) × 21 × 21 cm2
= 4158 cm2
Example 3:
The hollow sphere, in which the circus motorcyclist performs his stunts, has a diameter of 7 m. Find the area available to the motorcyclist for riding.
Answer:
Diameter of the sphere = 7 m. Therefore, radius r is 3.5 m.
Now, the riding space available for the motorcyclist is the surface area of the ‘sphere’.
Surface area of a sphere = 4πr2
= 4 × \(\frac{22}{7}\) × 3.5 × 3.5 m2
= 154 m2
Example 4:
A hemispherical dome of a building needs to be painted (see the given figure). If the circumference of the base of the dome is 17.6 m, find the cost of painting it. given the cost of painting is ₹ 5 per 100 cm2.
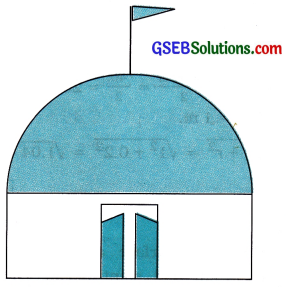
Answer:
Here, circumference of the dome 17.6 m.
Therefore, 17.6 m = 2πr.
So, the radius r of the dome
= 17.6 × \(\frac{7}{2 \times 22}\) m = 2.8m
Curved surface area of the hemispherical dome
= 2πr2
=2 × \(\frac{22}{7}\) × 2.8 × 2.8m2
= 49.28m2
Now, cost of painting 100 cm2 = 5.
∴ Cost of painting 1 m2 = 500.
(1m2 = 10000cm2)
Therefore, cost of painting 49.28 m2
= ₹ 500 × 49.28
= 24,640
Volume:
The measure of the space occupied by a solid object is called the volume of the object.
Capacity:
The volume of gas or liquid that can be contained by a hollow container is called the capacity of the container.
Volume of a cuboid = Area of the base × Height
= Length × Breadth × Height = l × b × h
Volume of a cube = Edge × Edge × Edge :
= a × a × a = a3
Usually, the volumes of gases and liquids are measured in litres (l), millilitres (ml) or kilolitres (kl).
- 1 m3 = 1000 litres
- 1 litre = 1000 cm3 = 1000 millilitres
- 1 m3 = 10,00,000 cm3 = 1 kilolitre
Example 1:
A wall of length 10 m was to be built across an open ground. The height of the wall is 4 m and thickness of the wall is 24 cm. If this wall is to be built up with bricks V whose dimensions are 24 cm × 12 cm × 8 cm, – how many bricks would be required?
Answer:
Here, we need to find the volume of the wall, which is nothing but a cuboid.
For the cuboidal wall, length l = 10 m = 1000 cm;
thickness b = 24 cm and height h = 4 m = 400 cm
∴ Volume of the wall = length × thickness × height
= 1000 × 24 × 400 cm3
Now, each brick is a cuboid with length l = 24 cm, breadth b = 12 cm and height h = 8 cm
So, volume of each brick = length x breadth x height = 24 × 12 × 8 cm3
Now, number of bricks required
= \(\frac{\text { volume of the wall }}{\text { volume of each brick }}\)
= \(\frac{1000 \times 24 \times 400}{24 \times 12 \times 8}\)
= 4166.6
So, the wall requires 4167 bricks.
Note: Here, all the measures of the wall are not multiples of the measures of the brick. Hence, the bricks are required to be broken. So, the answer received here cannot be considered to be proper.
![]()
Example 2:
A child playing with building blocks, which are of the shape of cubes, has built a structure as shown in the given figure. If the edge of each cube is 3 cm, find the volume of the structure built by the child.

Answer:
Volume of each cube = edge × edge × edge
= 3 × 3 × 3 cm3 = 27 cm2
The number of cubes In the structure =15
Then, the volume of the structure = 27 × 15 cm3
= 405 cm3
Volume of a cylinder = Area of base × Height
= πr2 × h
= πr2h
Here, r = radius of the cylinder and h = height of the cylinder.
Example 1:
The pillars of a temple are cylindrically shaped (see the given figure). If each pillar has a circular base of radius 20 cm and height 10 m, how much concrete mixture would be required to build 14 such pillars?

Answer:
The concrete mixture that is to be used to build up the pillars is the volume of the cylinders.
For each cylindrical pillar, radius r = 20 cm and
height h = 10 m = 1000 cm.
Volume of each cylindrical pillar = πr2h
= \(\frac{22}{7}\) × 20 × 20 × 1000 cm3
= \(\frac{8800000}{7}\) cm3
= \(\frac{8.8}{2}\)m3 (∵ 1000000 cm3 = 1 m3)
Then, volume of 14 pillars = volume of each pillar × 14
= \(\frac{8.8}{7}\) × 14 m3 = 17.6 m3
So, 14 pillars would need 17.6 m3 of concrete mixture.
Example 2:
At a Ramzan Mela, a stall keeper in one of the food stalls has a large cylindrical vessel of base radius 15 cm filled up to a height of 32 cm with orange juice. The juice is filled in small cylindrical glasses (see the given figure) of radius 3 cm up to a height of 8 cm and sold for? 15 each. How much money does the stall keeper receive by selling the juice completely?
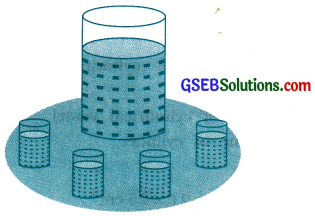
Answer:
For the juice in cylindrical vessel, radius R = 15 cm and height H = 32 cm.
Then, the volume of the juice in the vessel = πR2H
= π × 15 × 15 × 32 cm3
For, the juice in each cylindrical glass,
radius r = 3 cm and height h = 8 cm
Hence, the volume of the juice in each glass
= πr2h
= π × 3 × 3 × 8 cm3
So, number of glasses of juice that are sold
= \(\frac{\text { volume of the juice in the vessel }}{\text { volume of the juice in each glass }}\)
= \(\frac{\pi \times 15 \times 15 \times 32}{\pi \times 3 \times 3 \times 8}\)
= 100
Therefore, amount received by the stall keeper = ₹ 15 × 100
= ₹ 1500
Note: As this is a problem related to volume of liquid, there is no need to take the quotient of volumes measure-by-measure as \(\left(\frac{15}{3}\right) \times\left(\frac{15}{3}\right) \times\left(\frac{32}{8}\right)\)
Volume of a cone:
Volume of a cone = \(\frac{1}{3}\)πr2h; where r = radius of the cone and h = height of the cone
Example 1:
The height and the slant height of a cone are 21 cm and 28 cm respectively. Find the volume of the cone.
Answer:
For the given cone, height h = 21 cm and slant
height l = 28cm.
Now, l2 = r2 + h2
∴ r = \(\sqrt{l^{2}-h^{2}}=\sqrt{28^{2}-21^{2}}\) cm = 7 √7 cm
Then, volume of the cone
= \(\frac{1}{3}\)rr2h
= \(\frac{1}{3} \times \frac{22}{7}\) × 7 √7 × 7 √7 × 21 cm3
= 7546 cm3
Example 2:
Monica has a piece of canvas whose area is 551 m2. She uses it to have a conical tent made, with a base radius of 7 m. Assuming that all the stitching margins and L. the wastage incurred while cutting, amounts to approximately 1 m2, find the volume of the tent that can be made with It.
Answer:
Since, the area of the canvas = 551m2 and area of the canvas lost in wastage is 1 m2, the area of canvas actually used for making the tent is (551 – 1) m2 = 550 m2.
Hence, the curved surface area of the conical tent = 550 m2 and the radius of the conical tent r = 7 m
Curved surface area of tent = 550 m2
∴ πrl = 550
∴ \(\frac{22}{7}\) × 7 × l = 550
∴ l = \(\frac{550}{22}\) = 25 m
Now, l2 = r2 + h2
∴ h = \(\sqrt{l^{2}-r^{2}}\)
= \(\sqrt{25^{2}-7^{2}}\) m .
= \(\sqrt{625-49}\) m = √576 m = 24 m
So, the volume of the conical tent = \(\frac{1}{3}\)πr2h
= \(\frac{1}{3} \times \frac{22}{7}\) × 7 × 7 × 24 m3
= 1232 m3
![]()
Volume of a sphere:
Volume of a sphere = \(\frac{4}{3}\)πr3; where r = radius of the sphere
Volume of a hemisphere:
Volume of a hemisphere = \(\frac{2}{3}\)πr3; where r = radius of the hemisphere
Example 1:
Find the volume of a sphere of radius 11.2 cm.
Answer:
For the given sphere,
radius r = 11.2 cm.
Volume of a sphere
= \(\frac{4}{3}\)πr3
= \(\frac{4}{3} \times \frac{22}{7}\) × 11.2 × 11.2 × 11.2 cm3
= 5887.32 cm3
Example 2:
A shot-put is a metallic sphere of radius 4.9 cm. If the density of the metal is 7.8 g per cm3, find the mass of the shot-put.
Answer:
Since the shot-put is a solid sphere made of metal and its mass is equal to the product of its volume and density, we need to find the volume of the sphere.
For the given sphere, radius r = 4.9 cm.
Now, volume of a sphere
= \(\frac{4}{3}\)πr3
= \(\frac{4}{3} \times \frac{22}{7}\) × 4.9 × 4.9 × 4.9 cm3
= 493 cm3 (approx.)
Now, mass of 1 cm3 of metal is 7.8 g.
mass of the shot-put = 7.8 × 493 g
= 3845.4 g
= 3.85 kg (approx.)
Example 3:
A hemispherical bowl has a radius of 3.5 cm. What would be the volume of water it would contain?
Answer:
For the given hemispherical bowl, radius r = 3.5 cm.
Capacity of the hemispherical bowl = Volume of a hemisphere
= \(\frac{2}{3}\)πr3
= \(\frac{2}{3} \times \frac{22}{7}\) × 3.5 × 3.5 × 3.5 cm3
= 89.8 cm3