This GSEB Class 9 Maths Notes Chapter 14 Statistics covers all the important topics and concepts as mentioned in the chapter.
Statistics Class 9 GSEB Notes
Data:
The facts or figures, which are numerical or otherwise (i.e., qualitative), collected with a definite purpose are called data. Data is plural form of Latin word ‘Datum’.
Statistics:
Statistics is a branch of Mathematics in which extraction of meaningful information is studied. Thus, statistics deals with collection, organisation, analysis and interpretation of data. The word ‘statistics’ is used in two different contexts. In plural sense it means numerical data. In singular sense it mean the subject dealing in data analysis.
Collection of data:
Primary data: When the information is collected by the investigator herself or himself with a definite objective in her or his mind, the data obtained is called primary data.
Secondary data:
When the information is gathered from a source which already had the information stored, the data obtained is called secondary data.
Presentation of data:
When the data is collected by an investigator, it is not some systematic data. This data is called raw data. As soon as the work related to collection of data is over, the investigator has to find out ways to present them in a form which is meaningful, easily understood and gives its main features at a glance.
The numerical values representing the facts included in the data are called observations. As the observations take different values, that fact or information is called variable. Thus, different values of the variable are called observations.
![]()
Range:
The difference of the highest and the lowest values In the data Is called the range of the data.
Classification of data:
Ungrouped frequency distribution table : In a data, If some given fixed value of the variable occurs n Urnes, the frequency of that value is said to be n. When different values of a variable along with their corresponding frequencies are represented In a tabular form, that table is called ungrouped frequency distribution table or simply a frequency distribution table.
Class or Class interval:
To present a large amount of data so that a reader can make ‘ sense of it easily, the variable values are condensed into groups called classes or class intervals. The size of a class, i.e., the difference of the greatest and the smallest value of variable in that class, is called the class size or class width. In each of these classes, the least value is called the lower class limit and the greatest value is called the upper class limit. When different classes along with their corresponding frequencies are represented in a tabular form, that table is called a grouped frequency distribution table.
In a grouped frequency distribution table, there are two types of classes:
1. Non-overlapping classes: When the variable is discrete, meaning it takes certain finite values (mostly integer values) in some interval, the classes are so prepared that there is gap between the upper class limit of any class and the lower class limit of the next class, e.g., classes 1-10, 11-20, 21-30 etc.
Such classes are called non-overlapping classes. They include the lower class limit as well as the upper class limit.
2. Continuous classes: When the variable is continuous, meaning it can take any value (even fractional or decimal value) in some finite or infinite interval, the classes are so prepared that there is no gap between the upper class limit of any class and the lower class limit of the next class, e.g., classes 0-5, 5-10, 10-15, 15-20, …, etc. Such classes are called continuous classes. They include the lower class limit, but do not include the upper class limit. This means that if the given classes are 0-5, 5-10, 10-15, …, then the observation valued 5 will not be included in the class 0-5, but it will be included in class 5-10.
Similarly, the observation valued 10 will not be included in the class 5-10, but it will be included in the class 10-15.
To convert non-overlapping classes into continuous classes, half of the gap between the classes is added to the upper class limit and is subtracted from the lower class limit of each class.
Example 1.
Consider the marks obtained by 10 students in a mathematics test as given below:
55 36 95 73 60 42 25 78 75 62
Find the range of the data.
Answer:
Arranging the marks in the ascending order:
25 36 42 55 60 62 73 75 78 95
Now, it can easily be seen that the lowest marks are 25 and the highest marks are 95.
The difference of the highest and the lowest value in the data is called the range of the data.
Hence, the range of the given data = 95-25 I
= 70.
Example 2:
Consider the marks obtained (out of 100, marks) by 30 students of Class IX of a school:

Represent this data in a frequency distribution table.
Table 1
| Marks | Number of students (i.e., the frequency) |
| 10 | 1 |
| 20 | 1 |
| 36 | 3 |
| 40 | 4 |
| 50 | 3 |
| 56 | 2 |
| 60 | 4 |
| 70 | 4 |
| 72 | 1 |
| 80 | 1 |
| 88 | 2 |
| 92 | 3 |
| 95 | 1 |
| Total | 30 |
Table 1 is called an ungrouped frequency distribution table or simply a frequency distribution table.
Example 3:
100 plants each were planted in 100 schools during Van Mahotsava. After one month, the number of plants that survived were ; recorded as :
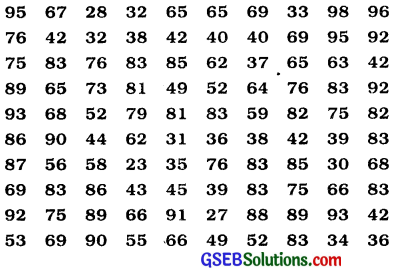
Present this data in a condensed tabular s form so that a reader can make sense of it easily.
Answer:
Since the data values vary from 23 to 98, we condense it into groups like 20 – 29, 30 – 39,…,90-99. These groupings are called ‘classes’; or ‘class intervals’, and their size is called the class size or class width, which is 10 in this case. In each of these classes, the least number is called the lower class limit and the greatest number is called the upper class limit, e.g., in 20-29, 20 is the ‘lower class limit’ and 29 is the ‘upper class limit’.
Also, recall that using tally marks, the data above can be condensed in tabular form as follows:
Table 2 :
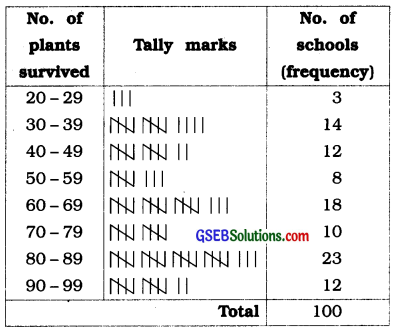
Presenting data in this form simplifies and condenses data and enables us to observe certain important features at a glance. This is called a grouped frequency distribution table. Here we can easily observe that 50% or more plants survived in 8+18+10 + 23 + 12 = 71 schools.
We observe that the classes in the table above are non-overlapping. Note that we could have made more classes of shorter size, or fewer classes of larger size also. For instance, the intervals could have been 22-26, 27-31, and so on. So, there is no hard and fast rule about this except that the classes should not overlap.
Example 4:
Let us now consider the following frequency distribution table which gives the weights of 38 students of a class:
Table 3
| Weight (in kg) | No. of students |
| 31-35 | 9 |
| 36-40 | 5 |
| 41-45 | 14 |
| 46-50 | 3 |
| 51-55 | 1 |
| 56-60 | 2 |
| 61-65 | 2 |
| 66-70 | 1 |
| 71-75 | 1 |
| Total | 38 |
Convert the classes of above frequency distribution to continuous classes to include two new students weighing 35.5 kg and 40.5 kg.
Answer:
Now, if two new students of weights 35.5 kg and 40.5 kg are admitted in this class, then T” in which interval will we include them? We cannot add them in the ones ending with 35 or 40, nor to the following ones. This is because there are gaps in between the upper and lower limits of two consecutive classes.
So, we need to divide the intervals so that the upper and lower limits of consecutive intervals are the same. For this, we find the difference between the upper limit of a class and the lower limit of its succeeding class.
We then add half of this difference to each of the upper limits and subtract the same from each of the lower limits.
For example, consider the classes 31-35 and 36 – 40.+
The lower limit of 36 – 40 = 36 The upper limit of 31 – 35 = 35 The difference = 36 – 35 = 1
Then, half the difference = \(\frac{1}{2}\) = 0.5
So the new class interval formed from 31-35 is (31-0.5)-(35 + 0.5),
i.e., 30.5-35.5.
Similarly, the new class formed from the class 36-40 is (36-0.5) – (40 + 0.5),
i.e., 35.5-40.5.
Continuing in the same manner, the continuous classes formed are :
30.5- 35.5, 35.5-40.5, 40.5-45.5, 45.5-50.5, 50.5- 55.5, 55.5-60.5, 60.5-65.5, 65.5-70.5, 70.5-75.5.
Now, it is possible for us to include the weights of the new students in these classes. But, another problem crops up because 35.5 appears in both the classes 30.5 – 35.5 and 35.5-40.5. In which class do you think this weight should be considered?
If it is considered in both classes, it will be counted twice.
By convention, we consider 35.5 in the class 35.5-40.5 and not in 30.5-35.5. Similarly, 40.5 is considered in 40.5-45.5 and not in
35.5-40.5.
So, the new weights 35.5 kg and 40.5 kg would be included in 35.5-40.5 and 40.5-45.5, respectively. Now, with these assumptions, the new frequency distribution table will be as shown below:
| Weight (in kg) | No. of students |
| 30.5-35.5 | 9 |
| 35.5-40.5 | 6 |
| 40.5-45.5 | 15 |
| 45.5-50.5 | 3 |
| 50.5-55.5 | 1 |
| 55.5-60.5 | 2 |
| 60.5-65.5 | 2 |
| 65.5-70.5 | 1 |
| 70.5 – 75.5 | 1 |
| Total | 40 |
Graphical representation of data:
The pictorial representation of data is called graphical representation of data. We shall study following graphical representations:
- Bar graph
- Histogram of uniform width and of varying width
- Frequency polygon
Bar graph:
Usually bars of uniform width are drawn with equal spacing between them on one axis (say, the x-axis) depicting the variable. The values of the variable Eire shown on the other axis (say, the y-axis) and the heights of the bars depend on the values of the variable. This type of representation is called the ‘Bar graph’.
Histogram:
This is a form of representation like the bar graph, but it is used for continuous class intervals.
There are two types of Histogram :
- Histogram of uniform width
- Histogram of varying width.
![]()
Histogram of uniform width:
- While drawing a histogram, the boundary point of classes with equal length are shown on the x-axis and the frequency is shown on the y-axis, with convenient scale, on a graph paper.
- For a histogram, on each class, a column of height proportional to the frequency of that class is formed. Thus, the number of columns is equal to the number of classes. The figure so obtained is called histogram.
- Each column in a histogram is a rectangle whose base is equal to the class with boundary points and whose height is equal to the frequency.
Histogram of varying width:
While drawing a histogram, if the class lengths are unequal, we have to calculate the height of the rectangle proportionately. For that, the following formula will be used:
Height of the rectangle
= \(\frac{\text { Frequency of a given class }}{\text { Class length of the given class }}\) × Class length of the class with minimum class length
In this type of histogram, the widths of the rectangles will be different and the area of the rectangles (not just height) will represent the frequencies.
Frequency polygon:
- The class mark of each class of frequency distribution is shown on the x-axis. The frequency corresponding to the class mark is shown on the y-axis.
Class mark = \(\frac{\text { Upper limit + Lower limit }}{2}\) - We take two virtual classes, one before the first and the second after the last. The frequency of each of these classes is taken as 0. The points with class mark of these classes (and corresponding frequencies 0) are also shown on the graph. Thus, the number of class marks to be shown will be 2 more than the number of classes.
- The points obtained are joined by line segments in order. The graph thus obtained is called the frequency polygon of the given distribution. The frequency polygon forms a closed figure with the x-axis.
- If a histogram is drawn for the given continuous frequency distribution, then joining the midpoints of the top sides of rectangles in order with two virtual points on the x-axis gives the frequency polygon of the given distribution.
- If the leading (initial or first) class does not start from zero, to adjust to the scale utilized, we mark a kink or a break on any of the axes.
Example 1:
In a particular section of Class IX, 40 students were asked about the month of / their birth and the following graph was prepared for the data so obtained:

Observe the bar graph given above and answer the following questions:
(i ) How many students were born in the month of November?
Answer:
4 students were born in the month of November
(ii) In which month were the maximum number of students bom?
Answer:
The maximum number of students were born in the month of August.
Example 2:
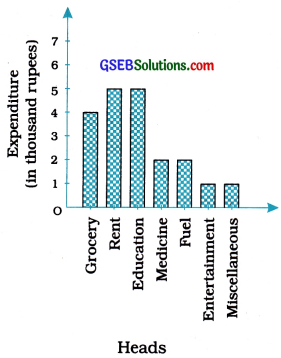
A family with a monthly income of ₹ 20,000 had planned the following expenditures per / month under various heads :
| Heads | Expenditure (in thousand rupees) |
| Grocery | 4 |
| Rent | 5 |
| Education of children | 5 |
| Medicine | 2 |
| Fuel | 2 |
| Entertainment | 1 |
| Miscellaneous | 1 |
Draw a bar graph for the data above.
Answer:
We draw the bar graph of this data in the following steps. Note that the unit in the second column is thousand rupees. So, ‘4’ against ‘Grocery’ means ₹ 4000.
- We represent the Heads (variable) on the horizontal axis choosing any scale, since the width of the bar is not important. But for clarity, we take equal widths for all bars and maintain equal gaps in between. Let one Head be represented by one unit.
- We represent the expenditure (value) on the vertical axis. Since the maximum expenditure is ₹ 5000, we can choose the scale as 1 unit = ₹ 1000.
- To represent our first Head, i.e., grocery, we draw a rectangular bar with width 1 unit and height 4 units.
- Similarly, other Heads are represented leaving a gap of 1 unit in between two consecutive bars.
The bar graph is shown In the following figure:
Histogram:
This is a form of representation like the bar graph, but it is used for continuous class intervals. For instance, consider the frequency distribution Table 6, representing the weights of 36 students of a class :
| Weights (in kg) | Number of students |
| 30.5-35.5 | 9 |
| 35.5-40.5 | 6 |
| 40.5-45.5 | 15 |
| 45.5-50.5 | 3 |
| 50.5-55.5 | 1 |
| 55.5-60.5 | 2 |
| Total | 36 |
Let us represent the data given above graphically as follows :
1. We represent the weights on the horizontal axis on a suitable scale. We can choose the scale as 1 cm = 5 kg. Also, since the first class interval is starting from 30.5 and not zero, we show it on the graph by marking a kink or a break on the axis.
2. We represent the number of students (frequency) on the vertical axis on a suitable scale. Since the, maximum frequency is 15, we need to choose the scale to accomodate this maximum frequency.
3. We now draw rectangles (or rectangular bars) of width equal to the class-size and lengths according to the frequencies of the corresponding class intervals. For example, the rectangle for the class interval 30.5 – 35.5 will be of width 1 cm and length 9 cm.
4. In this way, we obtain the graph as shown in the given figure :
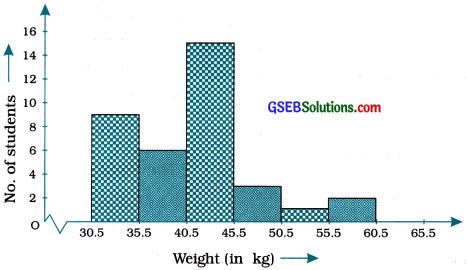
Observe that since there are no gaps between consecutive rectangles, the resultant graph appears like a solid figure. This is called a histogram, which is a graphical representation of a grouped frequency distribution with continuous classes. Also, unlike a bar graph, the width of the bar plays a significant role in its construction.
Here, in fact, areas of the rectangles erected are proportional to the corresponding frequencies. However, since the widths of the rectangles are all equal, the lengths of the rectangles are proportional to the frequencies. That is why, we draw the lengths according to (3) above.
![]()
Example 1:
A teacher wanted to analyse the performance of two sections of students in a mathematics test of 100 marks. Looking at their performances, she found that a few students got under 20 marks and a few got 70 marks or above. So she decided to group them into intervals of varying sizes as follows :
0-20, 20-30, ………., 60-70, 70-100
Then she formed the following table:
| Marks | Number of students |
| 0-20 | 7 |
| 20-30 | 10 |
| 30-40 | 10 |
| 40-50 | 20 |
| 50-60 | 20 |
| 60-70 | 15 |
| 70-100 | 8 |
| Total | 90 |
Answer:
A histogram for this table was prepared by a student as shown in the given figure.
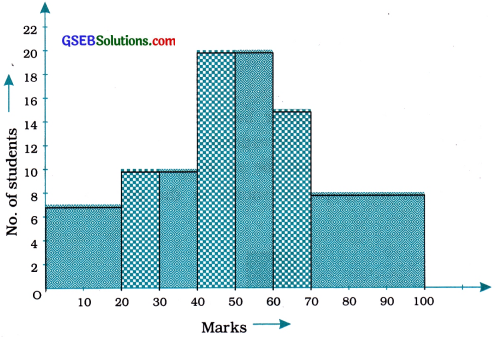
Carefully examine this graphical representation. Do you think that it correctly represents the data? No, the graph is giving us a misleading picture. As we have mentioned earlier, the areas of the rectangles are proportional to the frequencies in a histogram. Earlier this problem did not arise, because the widths of all the rectangles were equal. But here, since the widths of the rectangles are varying, the histogram above does not give a correct picture. For example, it shows a greater frequency in the interval 70-100, than in 60-70, which is not the case.
So, we need to make certain modifications in ‘ the lengths of the rectangles so that the areas ‘[ are again proportional to the frequencies.
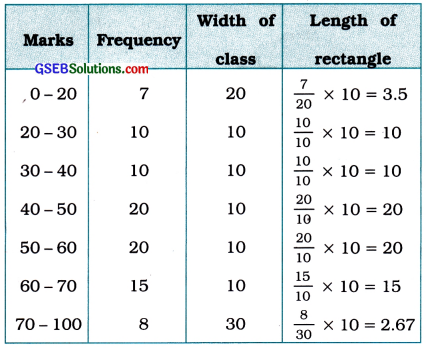
The steps to be followed are as given below:
- Select a class interval with the minimum class size. In the example above, the minimum class size is 10.
- The lengths of the rectangles are then modified to be proportionate to the class size 10.
For instance, when the class size is 20, the length of the rectangle is 7. So when the class size is 10, the length of the rectangle
will be \(\frac{7}{20}\) × 10 = 3.5.
Similarly, proceeding in this manner, we get the following table :
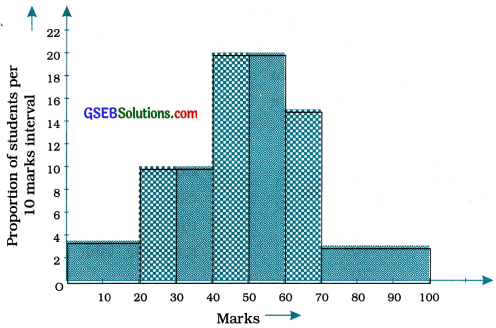
Example 2:
Consider the marks, out of 100, obtained by 51 students of a class in a test, given in Table.
| Marks | No. of students |
| 0-10 | 5 |
| 10-20 | 10 |
| 20-30 | 4 |
| 30-40 | 6 |
| 40-50 | 7 |
| 50-60 | 3 |
| 60-70 | 2 |
| 70-80 | 2 |
| 80-90 | 3 |
| 90-100 | 9 |
| Total | 51 |
Draw a frequency polygon corresponding to this frequency distribution table.
Answer:
Let us first draw a histogram for this data and mark the midpoints of the tops of the rectangles as B, C, D, E, F, G, H, I, J, K, respectively. Here, the first class is 0-10. So, to find the class preceding 0-10, we extend the horizontal axis in the negative direction and find the midpoint of the imaginary class interval (-10)-0. The first endpoint, i.e., B is joined to this midpoint with zero frequency on the negative direction of the horizontal axis. The point where this line segment meets the vertical axis is marked as A. Let L be the midpoint of the class succeeding the last class of the given data. Then OABCDEFGHIJKL is the frequency polygon, which is shown in the following figure.
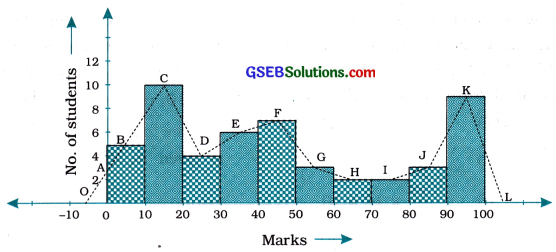
Frequency polygon can also be drawn independently without drawing histogram. For this, we require the midpoints of the class intervals used in the data. These midpoints of the class intervals are called class marks.
To find the class mark of a class interval, we find the sum of the upper limit and lower limit of a class and divide it by 2. Thus,
Class mark = \(\frac{\text { Upper } \text { limit + Lower limit }}{2}\)
Example 3:
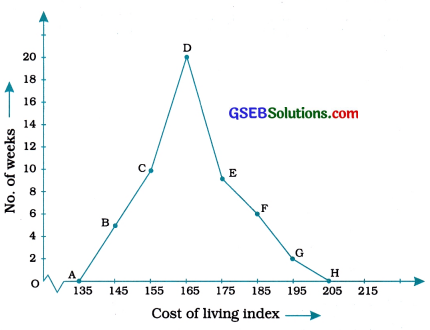
In a city, the weekly observations made in a study on the cost of living index are given in the following table:
| Cost of living Index | No. of weeks |
| 140- 150 | 5 |
| 150-160 | 10 |
| 160-170 | 20 |
| 170-180 | 9 |
| 180-190 | 6 |
| 190-200 | 2 |
| Total | 52 |
Draw a frequency polygon for the data above (without constructing a histogram).
Answer:
Since we want to draw a frequency polygon without a histogram, let us find the class marks of the classes given above, that is of 140-150, 150-160,…
For 140-150, the upper limit = 150, and the lower limit =140
So, the class mark = \(\frac{150+140}{2}=\frac{290}{2}\) = 145.
Continuing in the same manner, we find the class marks of the other classes as well. So, the new table obtained is as shown in the following table :
| Class | Classmark | Frequency |
| 140- 150 | 145 | 5 |
| 150-160 | 155 | 10 |
| 160-170 | 165 | 20 |
| 170- 180 | 175 | 9 |
| 180- 190 | 185 | 6 |
| 190-200 | 195 | 2 |
| Total | 52 | |
We can now draw a frequency polygon by plotting the class marks along the horizontal axis, the frequencies along the vertical axis, and then plotting and joining the points B(145, 5), C(155, 10), D (165, 20), E (175, 9), F (185, 6) and G (195, 2) by line segments. We should not forget to plot the point corresponding to the class mark of the class 130- 140 (just before the lowest class 140- 150) with zero frequency, that is, A (135, 0), and the point H (205, 0) occurs immediately after G(195, 2).
So, the resultant frequency polygon will be ABCDEFGH (see the given figure).
![]()
Measures of central tendency:
- A measure of central tendency of given data is a number which has the characteristics of the whole data and which represents the total data.
- There are three measures of central tendency:
- Mean,
- Median and
- Mode.
Mean (x̄):
The mean or average of a number of observations is the sum of the values of all the observations divided by the total number of observations. It is denoted by x̄ (read as x bar).
So, if x1, x2, x3, …….. xn are observations, then the mean of these observations is x̄ given by x̄ =\(\frac{x_{1}+x_{2}+x_{3}+\ldots+x_{n}}{n}\)
We use the Greek alphabet X (read as sigma) as a symbol for summation. Instead of writing x1 + x2 + x3 + … + xn, we write \(\sum_{i=1}^{n}\) xi
which is read as “the sum of x, as i varies from 1 to n”.
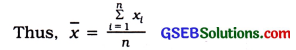
If the observations are large, we can use the method of assumed mean with following formula:
x̄ = A + \(\frac{\sum_{i=1}^{n} d_{l}}{n}\) where, A = assumed mean,
dt = xi – A for all i and n = total number of observations.
Mean of discrete frequency distribution:
The mean of a discrete frequency distribution in which the scores x1, x2, x3, …, xk has corresponding frequencies f1, f2, f3 …, fk respectively can be obtained by the following formula :
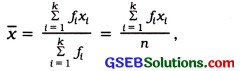
where, x̄ = mean
fixi = the product of I th observation and corresponding frequency
Σfi = n = total frequency
The same formula can be used for a continuous frequency distribution for which xi will represent the class mark of ith class.
In the calculations of mean of a grouped data, if the values of obseryation/central value or frequencies are very large or very small, the method of assumed mean is utilized to simplify the calculations.
Properties of Mean:
- Definition of mean is precise.
- All observations of the data are used in calculation of the mean of discrete frequency distribution and so the mean is a typical measure giving an overall idea of the total data.
- The greatest and the smallest observations have strong influence on the mean. The mean can be considered to be a stable measure if the range (the difference between the greatest and the smallest of the observations) is small.
- Subtracting the mean from each observation of the data gives the ‘deviation from mean’. The sum of all deviations from mean is always zero, that is, S(xi – x̄) = 0.
- The change in every observation induces a similar change in the mean.
If yi = axi + b for all i, then y = ax + b, a, b are real numbers and a ≠ 0. The algebraic operations may be carried out in any order. - We can do algebraic operations on mean, such as addition, subtraction, multiplication and division, and its formula \(\frac{\Sigma x_{i}}{n}\) is algebraic.
If any two of the three quantities Σxi (the sum of all observations), n (the number of observations) and x̄ (the mean) are given, the third can be obtained.
If the mean of n observations of one data is x̄, the sum of the observations is n x̄. If the mean of m observations of another data is ȳ, the sum of these m observations is mȳ. Hence, the sum of (n + m) observations is nx̄ + mȳ.
The combined (mixed) mean of two data is \(\frac{n \bar{x}+m \bar{y}}{n+m}\)
Note: The combined mean of more than two data can be defined in the same manner.
Median (M):
After arranging the observations in ascending or descending order, the observation which is obtained in the middle is called the median. It is denoted by M.
If the number of observations (n) is odd, then
median M = \(\frac{n + 1}{2}\)th observation
If the number of observations (n) is even, then

Mode (Z):
The observation which is repeated most often in an ungrouped data is called the mode of the data. It is denoted by Z.
If no observation in the data is repeated in an ungrouped data, we say the data has no mode, i.e., the mode is absent. If there are two or more observations in a data that are repeated most often and the same number of times, each such observation is a mode. A data with one mode is called unimodal data. A data with exactly two modes is called bimodal data, while a data with more than two modes is called multimodal data.
Example 1:
5 people were asked about the time in a week they spend in doing social work in their community. They said 10, 7, 13, 20 and 15 hours, respectively. Find the mean (or average) time in a week devoted by them for social work.
Answer:
Mean = \(\frac{\text { Sum of all the observations }}{\text { Total number of observations }}\)
To simplify our working of finding the mean, let us use a variable x( to denote the ith observation. In this case, i can take the values from 1 to 5. So our first observation is x1 second observation is x2, and so on till x5. Also x1 = 10 means that the value of the first observation, denoted by x1 is 10. Similarly, x2 = 7, x3 = 13, x4 = 20 and x5 = 15.
Therefore, the mean

= 13
So, the mean time spent by these 5 people in doing social work is 13 hours in a week.
Example 2:
Find the mean of the marks obtained by 30 students of Class IX of a school, given in sum no. 2 of “Sums of Enrich ‘Remember’.”
Answer:
x̄ = \(\frac{x_{1}+x_{2}+\ldots+x_{30}}{30}\)
\(\sum_{t=1}^{30} x_{i}\) = 10 + 20 + 36 + 92 + 95 + 40 + 50 + 56 + 60 + 70 + 92 + 88 + 80 + 70 + 72 + 70 + 36 + 40 + 36 + 40 + 92 + 40 + 50 + 50 + 56 + 60 + 70 + 60 + 60 + 88 = 1779
So x̄ = \(\frac{1779}{30}\) = 59.3
Note that we have formed a frequency table for this data (see table 1).
The table shows that 1 student obtained 10 marks, 1 student obtained 20 marks, 3 students obtained 36 marks, 4 students obtained 40 marks, 3 students obtained 50 marks, 2 students obtained 56 marks, 4 students obtained 60 marks, 4 students obtained 70 marks, 1 student obtained 72 marks, 1 student obtained 80 marks, 2 students obtained 88 marks, 3 students obtained 92 marks and 1 student obtained 95 marks.
So, the total marks obtained = (1 × 10) + (1 × 20) + (3 × 36) + (4 × 40) + (3 × 50) + (2 × 56) + (4 × 60) + (4 × 70) + (1 × 72) + (1 × 80) + (2 × 88) + (3 × 92) +(1 × 95)
= f1x1 + ……….. + f13x13; where, Jt is the frequency of the ith entry in table 1.
In brief, we write this as \(\sum_{t=1}^{13}\)fixi.
So, the total marks obtained
= \(\sum_{t=1}^{13}\)fixi.
= 10 + 20 + 108 + 160 + 150+ 112 + 240 + 280 + 72 + 80 + 176 + 276 + 95 .
= 1779
Now, the total number of observations 13
= \(\sum_{t=1}^{13}\)fi.
=f1 + f2 + – + f13
= 1 + 1 + 3 + 4 + 3 + 2 + 4 + 4 + 1 + 1 + 2 + 3 + 1
= 30
So, the mean x̄ = \(\frac{\text { Sum of all the observations }}{\text { Total number of observations }}\)
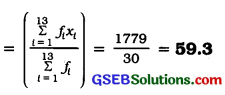
This process can be displayed In the following table, which is a modified form of a table.
| Marks (xi) | Number of students (fi) | fixi |
| 10 | 1 | 10 |
| 20 | 1 | 20 |
| 36 | 3 | 108 |
| 40 | 4 | 160 |
| 50 | 3 | 150 |
| 56 | 2 | 112 |
| 60 | 4 | 240 |
| 70 | 4 | 280 |
| 72 | 1 | 72 |
| 80 | 1 | 80 |
| 88 | 2 | 176 |
| 92 | 3 | 276 |
| 95 | 1 | 95 |
| Total | \(\sum_{t=1}^{13} f_{i}\) = 30 | \(\sum_{t=1}^{13} f_{i} x_{i}\) = 1779 |
Example 3:
The heights (in cm) of 9 students of a class are as follows:
155, 160, 145, 149, 150, 147, 152, 144, 148
Find the median of this data.
Answer:
First of all we arrange the data in the ascending order, as follows:
144, 145, 147, 148, 149, 150, 152, 155, 160 Since the number of students is 9, an odd number, we find out the median by finding the height of the \(\left(\frac{n+1}{2}\right) \text { th }=\left(\frac{9+1}{2}\right)\)th = the 5th student, which is 149 cm.
So, the median, i.e., the medial height is 149 cm.
Example 4:
The points scored by a Kabaddi team in a series of matches are as follows:
17, 2, 7, 27, 15, 5, 14, 8, 10, 24, 48, 10, 8, 7, 18, 28
Find the median of the points scored by the team.
Answer:
Arranging the points scored by the team in the ascending order, we get 2, 5, 7, 7, 8, 8, 10, 10, 14, 15, 17, 18, 24, 27, 28, 48
There are 16 terms. So there are two middle terms, i.e., the \(\frac{16}{2}\) th and (\(\frac{16}{2}\) + 1)th,
i. e., the 8th and 9th terms.
So, the median is the mean of the values of the 8th and 9th terms.
i.e., the median = \(\frac{10 + 14}{2}\) = 12
So, the medial points scored by the Kabaddi team is 12.
Example 5:
Find the mode of the following marks (out of 10) obtained by 20 students:
4, 6, 5, 9, 3, 2, 7, 7, 6, 5, 4, 9, 10, 10, 3, 4, 7, 6, 9, 9
Answer:
We arrange this data in the ascending prder as below:
2, 3, 3, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7, 7, 9, 9, 9, 9, 10, 10
Here 9 occurs most frquently, i.e., four times. So, the mode is 9.
![]()
Example 6:
Consider a small unit of a factory where there are 5 employees: a supervisor and four labourers. The labourers draw a salary of
₹ 5,000 per month each while the supervisor gets ₹ 15,000 per month. Calculate the mean, median and mode of the salaries of this unit of the factory.
Answer:
Mean = \(\frac{5000+5000+5000+5000+15000}{5}\)
= \(\frac{35000}{5}\)
= 7000
So, the mean salary is ₹ 7000 per month. To obtain the median, we arrange the salaries in the ascending order:
5000, 5000, 5000, 5000, 15000
Since the number of employees in the factory is 5, the median is given by the \(\frac{5 + 1}{2}\) th = \(\frac{6}{2}\) th = 3rd observation.
Therefore, the median is ₹ 5000 per month. To find the mode of the salaries, i.e., the modal salary, we see that 5000 occurs the maximum number of times in the data 5000, 5000, 5000, 5000, 15000. So, the modal salary is ₹ 5000 per month.