This GSEB Class 9 Maths Notes Chapter 6 Coordinate Geometry covers all the important topics and concepts as mentioned in the chapter.
Coordinate Geometry Class 9 GSEB Notes
Line segment:
A part (or portion) of a line with two end points is called a line segment.
Ray:
A part of a line with one end point is called a ray.
Note: The line segment AB is denoted by \(\overline{\mathrm{AB}}\) and its length is denoted by AB. The ray AB is denoted by \(\overrightarrow{\mathrm{AB}}\) and the line AB is denoted by \(\overleftrightarrow{\mathrm{AB}}\). However, we will not use these symbols, and will denote line segment AB, ray AB, length AB and line AB by the same symbol AB. The meaning will be clear from the context. Sometimes small letters I, m, n, etc. will be used to denote lines.
Collinear points and non-collinear points:
If three or more points lie on the same line, they are called collinear points; otherwise they are called non-collinear points.
Angle, arms and vertex:
An angle is formed when two distinct rays originate from the same end point. The rays making an angle are called the arms of the angle and the common end point is called the vertex of the angle.
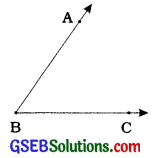
Here, two distinct rays BA and BC with the common end point B form angle ABC. Angle ABC is symbolically written as ∠ ABC. Symbol ∠ ABC also denotes the degree measure of ∠ABC. Rays BA and BC are arms of ∠ABC and point B is the vertex of ∠ABC.
Types of angles:
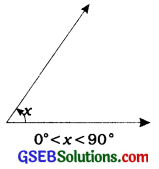
1. Acute angle: An angle which measures between 0° and 90° is called an acute angle.
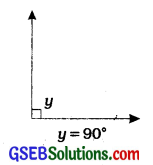
2. Right angle: An angle which measures exactly 90° is called a right angle.
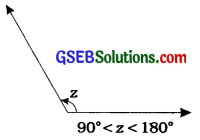
3. Obtuse angle: An angle which measures between 90° and 180° is called an obtuse angle.
4. Straight angle: An angle which measures exactly 180° is called a straight angle.
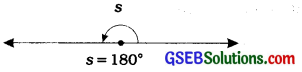
5. Reflex angle:An angle which measures between 180° and 360° is called a reflex angle
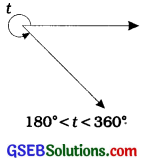
Thus, an acute angle lies between 0° and 90°, a right angle is equal to 90°, an obtuse angle lies between 90° and 180°, a straight angle is equal to 180° and a reflex angle lies between 180° and 360°.
Complementary angles:
Two angles whose sum is 90° are called complementary angles.
![]()
Supplementary angles:
Two angles whose sum is 180° are called supplementary angles.
If ∠A = 40°, ∠B = 50° and ∠C = 140°, then ∠A and ∠B are complementary angles while ∠A and ∠C are supplementary angles.
Adjacent angles:
Two angles are adjacent, if they have a common vertex, a common arm and their non-common arms are on different sides of the common arm.
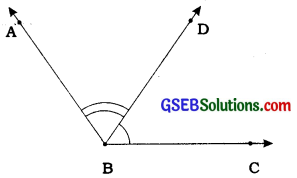
Here, ∠ABD and ∠DBC are adjacent angles. Ray BD is their common arm and B is their common vertex. Ray BA and ray BC are their non-common arms.
When two angles are adjacent, their sum is always equal to the angle formed by the two non-common arms.
Here, ∠ABC = ∠ABD + ∠DBC
Linear pair of angles:
In two adjacent angles, if their non-common arms form a line, then they are called linear pair of angles or angles of a linear pair.
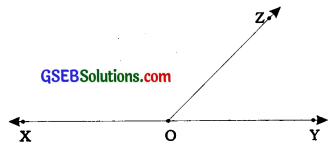
Here, in case of adjacent angles ∠XOZ and ∠ZOY, their non-common arms OX and OY form line XY. Hence, ∠XOZ and ∠ZOY are angles of a linear pair. Their sum is always 180°.
Here, ∠ XOZ + ∠ ZOY = 180°
Vertically opposite angles:
Two angles having a common vertex and each arm of the first angle forming a line with an arm of the other angle are called vertically opposite angles.
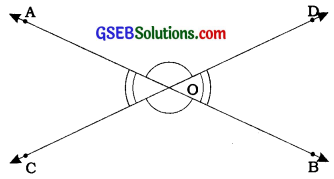
Here, lines AB and CD intersect at O. Then, we get two pairs of vertically opposite angles. ∠AOC and ∠BOD form one pair of vertically opposite angles. Similarly, ∠AOD and ∠BQC form the other pair of vertically opposite angles.
Vertically opposite angles are always equal.
Here, ∠AOC = ∠BOD and ∠AOD = ∠BOC.
Axiom 6.1: If a ray stands on a line, then the sum of two adjacent angles so formed is 180°.
Axiom 6.2: if the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.
For obvious reasons, the two axioms above together is called the Linear Pair Axiom.
Theorem 6.1:
If two lines intersect each other, then the vertically opposite angles are equal.
Example 1:
In the given figure, lines P9 and RS intersect each other at point O. If ∠POR: ∠ROQ = 5:7, find all the angles.
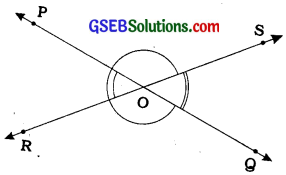
Answer:
∠POR + ∠ ROQ = 180° (Linear pair of angles)
But, ∠ POR: ∠ ROQ = 5:7 (Given)
∴ ∠POR = \(\frac{5}{12}\) × 180° = 75°
Similarly, ∠ R09 = \(\frac{7}{12}\) × 180° = 105°
Now, ∠ POS = ∠ ROQ = 105° (Vertically opposite angles)
and ∠ SOQ = ∠ POR = 75° (Vertically opposite angles)
Example 2:
In the given figure, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ respectively. If ∠POS = x, find ∠ROT.
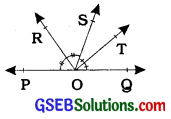
Answer:
Ray OS stands on the line POQ.
∴ ∠POS + ∠SOQ = 1800
But, ∠POS=x
∴ x + ∠SOQ=180°
SOQ = 180° – x
Now, ray OR bisects ∠POS.
∠ROS = \(\frac{1}{2}\) × ∠POS
= \(\frac{1}{2}\) × x = \(\frac{x}{2}\)
Similarly. ∠SOT = \(\frac{1}{2}\) × ∠SOQ
= \(\frac{1}{2}\) X (180°-x)
= 90°- \(\frac{x}{2}\)
Now. ∠ROT = ∠ROS + ∠SOT
= \(\frac{x}{2}\) + 90° – \(\frac{x}{2}\)
= 90°
Example 3:
In the given figure, OP, OQ, OR and OS are four rays. Prove that ∠POQ + ∠QOR + ∠SOR + ∠POS = 360°.
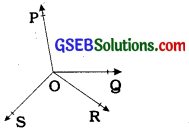
Answer:
Let us produce ray OQ backwards to a point T so that TOQ Is a line (See figure).
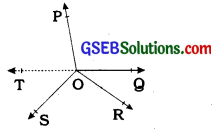
Now, ray OP stands on line TOQ.
∴ ∠TOP + ∠POQ = 1800 (Linear pair axiom) ………(1)
Similarly, ray OS stands on line TOQ.
∴ ∠TOS + ∠SOQ = 180° ………….(2)
But, ∠SOQ = ∠SOR + ∠QOR
So, (2) becomes ∠TOS + ∠SOR + ∠QOR = 180° ……….(3)
Now, adding (1) and (3), you get :
∠TOP + ∠POQ + ∠TOS + ∠SOR + ∠QOR = 360° ………..(4)
But, ∠TOP + ∠TOS = ∠POS
Therefore, (4) becomes
∠POQ + ∠QOR + ∠SOR + ∠POS = 360°
![]()
Parallel lines and a Transversal:
Transversal:
A line which intersects two or more lines at distinct points is called a transversal.
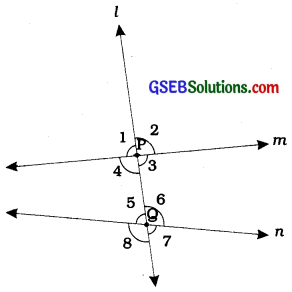
Here, line l intersects lines m and n at distinct points P and Q respectively. Hence, line l is a transversal for lines m and n. Four angles are formed at each of the points P and Q.
We name these angles as ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8 as shown in the figure.
Here, ∠1, ∠2, ∠7 and ∠8 are called exterior angles and ∠3, ∠4, ∠5 and ∠6 are called interior angles.
Corresponding angles:
Two angles, of which one is an exterior angles and the other is an interior angle on the same side of the transversal and not forming a linear pair are called corresponding angles.
Here, we have four pairs of corresponding angles as ∠1 and ∠5, ∠2 and ∠6, ∠4 and ∠8, ∠3 and ∠7.
Alternate interior angles:
Two interior angles lying on different sides of the transversal and not forming a linear pair are called alternate interior angles.
Here, ∠4 and ∠6 as well as ∠3 and ∠5 are alternate interior angles.
Many a times, alternate interior angles are referred as alternate angles.
Alternate exterior angles:
Two exterior angles lying on different sides of the transversal and not forming a linear pair are called alternate exterior angles.
Here, ∠1 and ∠7 as well as ∠2 and ∠8 are alternate exterior angles.
Interior angles on the same side of the transversal:
Two interior angles lying on the same side of the transversal are called interior angles on the same side of the transversal.
Here, ∠4 and ∠5, as well as ∠3 and ∠6, are interior angles on the same side of the transversal.
Interior angles on the same side of the transversal are also referred as consecutive interior angles or allied angles or co-interior angles.
Relation between the pairs of angles in case of parallel lines:
- Axiom 6.3: If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.
- Axiom 6.3 is referred as corresponding angles axiom.
- Axiom 6.4: If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel to each other.
Theorem 6.2:
If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.
Theorem 6.3:
If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
![]()
Theorem 6.4:
If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
Theorem 6.5:
If a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.
Lines parallel to the same line:
Theorem 6.6: Lines which are parallel to the same line are parallel to each other.
Example 1:
In the given figure 1, if PQ ∥ RS, ∠MXQ = 135° and ∠MYR = 40°, find ∠XMY.
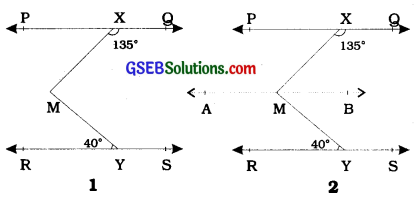
Draw a line AB parallel to line PQ, through point M as shown in figure 2.
Now, AB ∥ PQ and PQ ∥ RS.
Therefore, AB ∥ RS (∵ AB ∥ PQ and PQ ∥ RS);
Now, ∠QXM + ∠XMB = 180°
(AB II PQ, Interior angles on the same side of the transversal XM)
But, ∠QXM= 135°
∴ 135° + ∠XMB = 180°
∴ ∠XMB = 45° …………..(1)
Now, ∠BMY = ∠MYR (AB II RS; Atemate angled)
∴ ∠BMY = 40° …………..(2)
Adding (1) and (2), we get ∠XMB + ∠BMY = 45° + 40°
∴ ∠XMY = 85°
Example 2:
If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel.
Answer:
In the figure given below, a transversal AD intersects two lines PQ and RS at points B and C respectively. Ray BE is the bisector of ∠ABQ and ray CG is the bisector of ∠BCS; and BE ∥ CG.
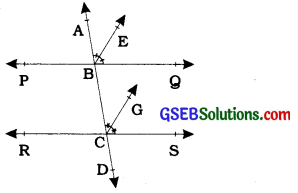
It is given that ray BE is the bisector of Z ABQ.
∴ ∠ ABE = \(\frac{1}{2}\)∠ABQ ………….(1)
Similarly, ray CG is the bisector of Z BCS.
∴ ∠BCG = \(\frac{1}{2}\)∠BCS ………… (2)
But, BE ∥CG and AD is the transversal.
∴ ∠ABE = ∠BCG (Corresponding angles axiom)
Substituting (1) and (2) in (3), we get
\(\frac{1}{2}\)∠ABQ = \(\frac{1}{2}\)∠BCS
∴ ∠ABQ = ∠BCS
But, they are the corresponding angles formed by transversal AD of PQ and RS; and are equal.
∴ PQ ∥ RS
(Converse of corresponding angles axiom)
Example 3:
In the given figure, AB ∥ CD and CD ∥ EE. Also EA ⊥ AB. If ∠BEF = 55°, find the values of x, y and z.
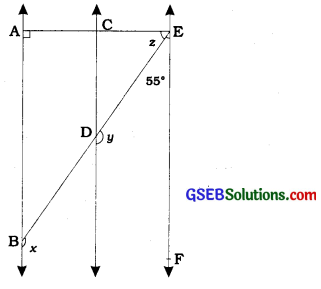
Answer:
y + 55° = 180°
(Interior angles on the same side of the transversal ED)
∴ y = 180°-55°
= 125°
Again, x = y (AB ∥ CD, Corresponding angles axiom)
∴ x = 125°
Now, since AB ∥ CD and CD ∥ EE therefore, AB ∥ EF.
So, ∠EAB + ∠FEA= 180° (Interior angles on the same side of the transversal EA)
Therefore, 90° + z + 55° = 180°
∴ z = 35°
Angle Sum Property of a mangle:
Theorem 6.7:
The sum of the angles of a triangle is 180°.
Exterior angle of a triangle:
In a triangle. if any side Is produced on one side, we get an angle which forms a linear pair with the angle of the triangle at the vertex where the side Is produced. This angle is called an exterior angle of a triangle.
In other words, an angle forming a linear pair with an angle of a triangle is called an exterior angle of the triangle.
![]()
Theorem 6.8:
If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
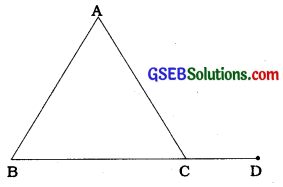
Here, ∠ACD is an exterior angle of ∆ABC and hence, ∠ACD = ∠A + ∠B.
Example 1:
In the given figure, if QT ⊥ PR, ∠TQR = 40° and ∠SPR = 30°, find x and y.
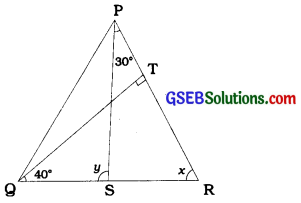
Answer:
In ∆ TQR, 90° + 40° + x = 180°
(Angle sum property of a triangle)
∴ x = 50°
Now, y – Z SPR + x (Theorem 6.8)
∴ y = 30° + 50°
∴ y = 80°.
Example 2:
In the given figure, the sides AB and AC of ∆ABC are produced to points E and D respectively. If bisectors BO and CO of ∠CBE and ∠BCD respectively meet at point O, then prove that ∠BOC = 90° \(\frac{1}{2}\)∠ BAC.
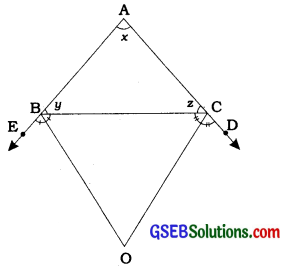
Answer:
Ray BO is the bisector of ∠CBE.
∠ CBO = \(\frac{1}{2}\)∠CBE
= \(\frac{1}{2}\)(180°- y)
= 90° – \(\frac{y}{2}\) ……….(1)
Similarly, ray CO is the bisector of ∠BCD.
∴ ∠ BCO = \(\frac{1}{2}\) ∠ BCD
= \(\frac{1}{2}\)(180°- z) = 90° – \(\frac{z}{2}\)
In ∆BOC, ∠BOC + ∠ BCO + ∠CBO = 180° ………(3)
Substituting (1) and (2) in (3), we get
∠BOC + 90°- \(\frac{z}{2}\) + 90°- \(\frac{y}{2}\) = 180°
∴∠BOC = \(\frac{z}{2}+ \frac{y}{2}\)
∴ ∠ BOC = \(\frac{1}{2}\) (y + z) ….(4)
But, x + y + z = 180°
(Angle sum property of a triangle):.y + z= 180°-x
Then, (4) becomes:
∠BOC = \(\frac{1}{2}\) (180°- x)
= 90°- \(\frac{x}{2}\)
= 90° – \(\frac{1}{2}\)∠BAC