Gujarat Board GSEB Solutions Class 10 Maths Chapter 1 Real Numbers Ex 1.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 1 Real Numbers Ex 1.1
Question 1.
Use Euclid’s division algorithm to find the HCF of
- 135 and 225
- 196 and 38220
- 867 and 255
Solution:
1. Let a = 225 and b = 135
Since a > b
Applying Euclid division Algorithm
a = bq + r (where 0 ≤ b < r)
225 = 135 × 1 + 90
Dividend = 225
Divisor = 135
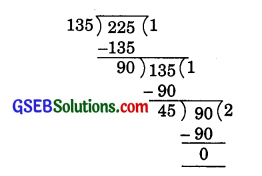
Since 90 is the remainder but 90 ≠ 0. So we apply Euclid division lemma to 135 and 90
a = bq + r (Here a = 135 and b = 90)
135 = 90 × 1 + 45
Since remainder 45 ≠ 0
So again, we apply Euclid division lemma to 90 and 45
a = bq + r (Here a = 90 and 6 = 45)
90 = 45 × 2 + 0
Since remainder is zero, the process stops. Since the divisor at this stage is 45, therefore HCF of 135 and 225 is 45.
![]()
2. Let a = 38220 and b = 196
Since a > b
Applying Euclid division lemma,
a = bq + r (where 0 ≤ r < b)
38220 = 196 × 195 + 0
Since remainder is zero, at this stage our process stops and divisor is 196,
Therefore 196 is the HCF.
3. Let a = 867 and b = 255
Since a > b
Applying Euclid division lemma
a = bq + r (where 0 ≤ b < r)
867 = 255 × 3 + 102
Since 102 ≠ 0, we apply Euclid division lemma to a = 255 and b = 102 we get
a = bq + r (where 0 ≤ b <r)
255 = 102 × 2 + 51
Since 51 ≠ 0 we apply Euclid division lemma to a = 102 and 6 = 51
a = bq + r
102 = 51 × 2 + 0
Since remainder is zero, our process stops. At this stage divisor is 51, therefore HCF is 51.
![]()
Question 2.
Show that any positive odd integer is of the form 6q + 1, or 6q + 3 or 6q + 5 where q is some integer.(CBSE)
Solution:
Let a be any positive integer and 6 = 6. Then by Euclid’s division algorithm,
a = 6q + r (0 ≤ r < 6) for some integer q > 0, the values of remainder must be less than 6, i.e.,
r = 0, 1, 2, 3, 4, 5
We take only odd numbers like 1, 3 and 5.
For r = 0, a = 6q + r = 6q + 0
⇒ a = 6q
⇒ a = 2(3q) = 3m
where m is any positive integer
∴ a = 6q (not odd)
Similarly,
for r = 2, a = 6q + 2 = 2 (3q + 1) (not odd)
for r = 4, a = 6q + 4 = 2 (3q + 2) (not odd)
for r = 6, a = 6q + 6 = 2 (3q + 3) (not odd)
But, for r = 1
a = 6q + 1
for r = 3
a = 6q + 3
and, for r = 5
a = 6q + 5
Thus, for r = 1, 3 and 5, a is odd.
So we take only odd value. Therefore any positive integer of the form of 617 + 1, 6q + 3 and 6q + 5 is odd.
![]()
Question 3.
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solution:
HCF of 616 and 32 will give the maximum number of columns in which they can march. Now we use Euclid’s Algorithm to find HCF.
Let a = 616 and b = 32
a = bq + r
616 = 32 × 19 + 8
Since 8 ≠ 0 we again apply Euclid’s Algorithm
a = bq + r
32 = 8 × 4 + 0
Since remainder is zero.
Hence the HCF of 616 and 32 is 8.
Therefore an army contingent can march in 8 columns each.
![]()
Question 4.
Use Euclid division lemma to show that the square of any positive integer is either of form 3m or 3m + 1 for some integer m.(CBSE)
[Hint: Let x be any positive integer then it is of the form 3q, 3q + 1 or 3q + 2. Now square each of these and show that they can be rewritten in the form of (3m or 3m + 1)]
Solution:
Let a be any positive integer and b = 3
By applying Euclid’s Algorithm
a = bq + r (0 ≤ r < 6)
then a = 3q + r (0 ≤ r < 3)
Values of r = 0, 1 and 2
when r = 0
then a = 3q + 0
a = 3q
when r = 1
then a = 3q + 1
when r = 2
then a = 3q + 2
![]()
Squaring of these positive integers as:
1. a = 3q
a2 = (3q)2
a2 = 9q2
a2 = 3 × (3q2)
a2 = 3m
Thus, 9q2 = 3 (3q2) is divisible by 3
2. a = 3q + 1
a2 = (3q + 1)2
a2 = 9q2 + 6q + 1
a2 = 3 (3q2 + 2q) + 1
(where, m = 3q2 + 2q)
= 3m + 1
Thus, a2 is written in the form of 3m + 1.
a = 3q + 2
a2 = (3q + 2)2
a2 = 9q2 + 12q + 4
a2 = 9q2 + 12q + 3 + 1
a2 = 3 (3q2 + 4q + 1) + 1
a2 = 3m + 1
where m = 3q2 + 4q + 1
Thus, a2 is written in the form of 3m + 1.
![]()
Question 5.
Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.(CBSE)
Solution:
Let a be any positive integer and b = 3
By Applying Euclid’s division lemma
a = bq + r (0 ≤ r < b)
then a = 3q + r (0 ≤ r < 3)
Values of r = 0, 1, 2
when r = 0
then a = 3q + 0
a = 3q
Cubing both sides
a3 = (3q)3
a3 = 27q3
a3 = 9 (3q3) [27q3 is divisible by 9]
a3 = 9m
when r = 1
a = 3q + 1
Cubing both sides
a3 = (3 q + 1)3
= 27q3 + 9q2 + 9q + 1
= 9 (3q3 + q2 + q) + 1
[27q3 + 9q2 + 9q is divisible by 9]
![]()
a3 = 9m + 1
when r = 2
a = 3q + 2
Cubing both sides
a3 = (3q + 2)3
= 27q3 + 54q2 + 36q + 8
= 9 (3q3 + 6q2 + 4q) + 8
[27q3 + 54q2 + 36q is divisible by 9]
a3 = 9m + 8
Therefore the cube of any positive integer is 9m, 9m + 1 or 9m + 8.