Gujarat Board GSEB Solutions Class 10 Maths Chapter 1 Real Numbers Ex 1.4 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 1 Real Numbers Ex 1.4
Question 1.
Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion.
- \(\frac{13}{3125}\)
- \(\frac{17}{8}\)
- \(\frac{64}{455}\)
- \(\frac{15}{1600}\)
- \(\frac{29}{343}\)
- \(\frac{23}{2^{3} \times 5^{2}}\)
- \(\frac{129}{2^{2} \times 5^{7} \times 7^{5}}\)
- \(\frac{6}{15}\)
- \(\frac{35}{50}\)
- \(\frac{77}{210}\)
Solution:
1. \(\frac{13}{3125}=\frac{13}{5^{5}}=\frac{13 \times 2^{5}}{5^{5} \times 2^{5}}\)
The denominator is of the form 2n × 5m.
Hence the decimal expansion of \(\frac{13}{3125}\) is terminating.

![]()
2. We can write \(\frac{17}{8}=\frac{17 \times 5^{3}}{2^{3} \times 5^{3}}=\frac{2125}{10^{3}}\)
the denominator is of the form 2n × 5m
Hence the decimal expansion \(\frac{17}{8}\) terminating.
3. \(\frac{64}{455}\)
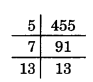
We can write it \(\frac{64}{5^{1} \times 7^{1} \times 13^{1}}\)
Since the denominator is not in the form of 2n × 5m and it also contains 7 and 13 as factors. Its decimal expansion will be non-terminating repeating.
4. \(\frac{15}{1600}\) = \(\frac{15}{2^{6} \times 5^{2}}\)
Denominator is of the form 2n × 5m

Hence the decimal expansion of \(\frac{15}{1600}\) is terminating.
5. \(\frac{29}{343}\) = \(\frac{29}{7^{3}}\)
Since the denominator is not in the form 2n × 5m and it also has 7 as factor then the decimal expansion of \(\frac{29}{343}\) is non-terminating repeating.
6. \(\frac{23}{2^{3} \times 5^{2}}\)
The denominator is of the form 2n × 5m then decimal expansion is terminating.
7. \(\frac{129}{2^{2} \times 5^{7} \times 7^{5}}\)
Since in denominator 7 is a factor. Hence the decimal expansion of \(\frac{129}{2^{2} \times 5^{7} \times 7^{5}}\) is non-terminating.
![]()
8. \(\frac{6}{15}\) = \(\frac{2 \times 3}{5 \times 3}=\frac{2}{5} \times \frac{2^{1}}{2^{1}}\)
Here denominator is in the form of 2n × 5m hence decimal expansion of \(\frac{6}{15}\) is terminating.
9. \(\frac{35}{50}\) = \(\frac{5 \times 7}{5 \times 5 \times 2}=\frac{7}{5^{2} \times 2^{1}}\)
Here denominator is in the form of 2n × 5m hence decimal expansion of \(\frac{35}{50}\) is terminating.
10. \(\frac{77}{210}\) = \(\frac{11 \times 7}{3 \times 7 \times 2 \times 5}=\frac{11}{3 \times 2 \times 5}\)
Since the denominator is not in the form of 2n × 5m and it also has 3 as a factor.
Then the decimal expansion of \(\frac{77}{210}\) is non-terminating.
Question 2.
Write down decimal expansions of the rational numbers in question 1 above which have terminating decimal expansions.
Solution:
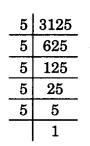
(i) \(\frac{13}{3125}\) = \(\frac{13 \times 2^{5}}{5^{5} \times 2^{5}}\)
= \(\frac{416}{100000}\)
(ii)

(iii)

(iv) \(\frac{23}{2^{3} \times 5^{2}}\) = \(\frac{23 \times 5}{2^{3} \times 5^{3}}\)
\(\frac{115}{1000}\) = 0.115
![]()
(v) \(\frac{6}{15}\) = \(\frac{2 \times 3}{5 \times 3}\)
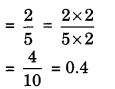
(vi) \(\frac{35}{60}\) = \(\frac{5 \times 7}{5 \times 5 \times 2}\)
\(=\frac{7}{5 \times 2}=\frac{7}{10}=0.7\)
Question 3.
The following real numbers have decimal expansions as given below. In each case decide whether they are rational or not. If they are rational and of the form \(\frac{p}{q}\) , what can you say about the prime factor of q?
- 43.123456789
- 0.120 1200 12000 120000 ……..
- 43.1\(\overline { 23456789 } \)
Solution:
1. 43.123456789 = \(\frac{43123456789}{10^{9}}\)
Since this number has a terminating decimal expansion. It is a rational number
of the form \(\frac{p}{q}\) and q is of the form 2n × 5m.
Hence prime factors of q are 2 and 5.
![]()
2. 0.120 1200 12000 120000 …
The decimal expansion is neither terminating nor recurring, therefore, the given number is an irrational number.
3. 43.1\(\overline { 23456789 } \)
Since the decimal expansion is non terminating recurring, the given number
is a rational number of the form \(\frac{p}{q}\) and q is not in the form of 2n × 5m i.e. the prime factors of q will also have a factor other them 2 or 5.