GSEB Solutions Class 10 Maths Chapter 13 પૃષ્ઠફળ અને ઘનફળ Ex 13.5

Gujarat Board GSEB Solutions Class 10 Maths Chapter 13 પૃષ્ઠફળ અને ઘનફળ Ex 13.5 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 13 પૃષ્ઠફળ અને ઘનફળ Ex 13.5

* આ સ્વાધ્યાય પરીક્ષાના હેતુથી બનાવેલ નથી.

પ્રશ્ન 1.
3 મિમી વ્યાસવાળા તાંબાના તારને 12 સેમી ઊંચાઈ અને 10 સેમી વ્યાસવાળા નળાકાર પર એવી રીતે વીંટવામાં આવે છે કે નળાકારની વક્રસપાટી સંપૂર્ણપણે ઢંકાઈ જાય છે, તો તારની લંબાઈ અને દળ શોધો. તાંબાની ઘનતા 8.88 ગ્રામ / સેમી³ સ્વીકારવામાં આવી છે.
ઉત્તર:
નળાકારની ઊંચાઈ = 12 સેમી = 120 મિમી
તારનો વ્યાસ 3 મિમી હોવાથી તારના એક આંટો નળાકારની ઊંચાઈમાંથી 3 મિમી જેટલા ભાગને ઢાંકી દેશે.
આથી નળાકારની વક્રસપાટીને સંપૂર્ણપણે ઢાંકી દેવા માટે તારના ૬ જરૂરી આંટાની સંખ્યા = \(\frac{120}{3}\) = 40.
નળાકારની ત્રિજ્યા r = = \(\frac{10}{2}\) સેમી = 5 સેમી
આથી નળાકાર ફરતે એક આંટો મારતા તારની લંબાઈ = નળાકારના પાયાનો પરિઘ = 2πr

= 2 × \(\frac{22}{7}\) × 5 સેમી
= \(\frac{220}{7}\) સેમી

આથી નળાકારની વસપાટીને સંપૂર્ણપણે ઢાંકી દેવા જરૂરી તારની લંબાઈ = H = (40 × \(\frac{220}{7}\)) સેમી = 1257.14 સેમી
તારની ત્રિજ્યા R = = \(\frac{3}{2}\) સેમી
= \(\frac{3}{2}\) સેમી

તારનું ઘનફળ = π R²H
= \(\frac{22}{7} \times \frac{3}{20} \times \frac{3}{20}\) × 1257.14 સેમી³
= 88.8978 સેમી³

તારનું દળ = ઘનફળ × ઘનતા
= (88.8978 × 8.88) ગ્રામ
= 789.41 ગ્રામ = 789 ગ્રામ (આશરે)
આમ, તારની લંબાઈ 1257.14 સેમી થાય અને તારનું દળ 789 ગ્રામ (આશરે) થાય.

પ્રશ્ન 2.
એક કાટકોણ ત્રિકોણની બાજુઓ 3 સેમી અને 4 સેમી (કર્ણ સિવાયની બાજુઓ) છે. તેને તેના કર્ણ આસપાસ પરિભ્રમણ કરાવવામાં આવે છે. તેનાથી પ્રાપ્ત થતા બે શંકુનું ઘનફળ અને તેમની સપાટીનું ક્ષેત્રફળ શોધો. (π ની કિંમત તમને અનુકૂળ પસંદ કરો.)
ઉત્તર:

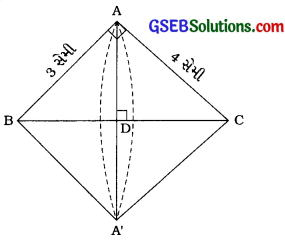
∆ ABCમાં, ∠A = 90°; AB = 3 સેમી અને AC = 4 સેમી
હવે, BC = \(\sqrt{\mathrm{AB}^{2}+\mathrm{AC}^{2}}\) (પાયથાગોરસ પ્રમેય)
= \(\sqrt{3^{2}+4^{2}}\) સેમી
= \(\sqrt{9+16}\) સેમી
= \(\sqrt{25}\) સેમી
= 5 સેમી
ધારો કે, AD ⊥ BC.
∆ ABCનું ક્ષેત્રફળ = \(\frac{1}{2}\) × AB × AC
= \(\frac{1}{2}\) × BC × AD
∴ AB × AC = BC × AD
∴3 × 4 = 5 × AD
∴ AD = \(\frac{12}{5}\) સેમી
AD = 2.4 સેમી
શંકુ BAA’ અને શંકુ CAA’ દ્વારા શંકુની જોડ રચાય છે.
શંકુ BAA’ માટે, ત્રિજ્યા r = AD = 2.4 સેમી, ઊંચાઈ h₁ = BD અને તિર્યક ઊંચાઈ l₁ = AB = 3 સેમી શ
ંકુ CAA’ માટે, ત્રિજ્યા r = AD = 2.4 સેમી, ઊંચાઈ h₂ = CD અને તિર્યક ઊંચાઈ l₂ = AC = 4 સેમી
શંકુની જોડનું ઘનફળ = શંકુ BAA’નું ઘનફળ + શંકુ CAA’નું ઘનફળ
= \(\frac{1}{3}\) πr²h₁ + \(\frac{1}{3}\) πr²h₂
= \(\frac{1}{3}\) πr²(h₁ + h₂)
= πr²(BD + CD)
= πr²(BC) (∵ BD + CD = BC)
= 5 × 3.14 × (2.4)² × 5 સેમી³ (π = 3.14 લેતાં)
= 30.14 સેમી³

શંકુની જોડની સપાટીનું ક્ષેત્રફળ = શંકુ BAA’ ની વક્ર સપાટીનું ક્ષેત્રફળ + શંકુ CAA’ ની વક્રસપાટીનું ક્ષેત્રફળ
= πrl₁ + πrl₂
= r (l₁ + l₂)
= 3.14 × 2.4 (3 + 4) સેમી²
= 52.75 સેમી²
આમ, શંકુની જોડનું ઘનફળ 30.14 સેમી થાય અને તેની સપાટીનું ક્ષેત્રફળ 32.75 સેમી થાય.

પ્રશ્ન 3.
એક ટાંકીનાં આંતરિક માપ 150 સેમી × 120 સેમી × 110 સેમી છે. તેમાં 129600 સેમી³ પાણી છે. ટાંકી પૂરેપૂરી ભરાય ન જાય ત્યાં સુધી તે પાણીમાં છિદ્રવાળી ઈંટો નાખવામાં આવે છે. પ્રત્યેક ઈટ તેના \(\frac{1}{17}\) ઘનફળ જેટલું પાણી શોષી લે છે. પ્રત્યેક ઈંટનું માપ 2.5 સેમી × 7.5 સેમી × 6.5 સેમી છે, તો પાણી બહાર ન આવે તે રીતે તે ટાંકીમાં કેટલી ઈંટો નાખી શકાય?
ઉત્તર:
લંબઘનાકાર ટાંકી માટે, લંબાઈ l = 150 સેમી, પહોળાઈ b = 120 સેમી અને ઊંચાઈ h = 110 સેમી
લંબઘનાકાર ટાંકીનું ઘનફળ = lbh
= 150 × 120 × 110 સેમી³
= 1980000 સેમી³
ટાંકીમાં રહેલ પાણીનું ઘનફળ = 129600 સેમી³
∴ ઈંટો નાખવાથી ખસતા પાણી દ્વારા ભરવાનો બાકી રહેતા ટાંકીના ભાગનું ઘનફળ = (1980000 – 129600) સેમી³
= 1850400 સેમી³
લંબઘનાકાર ઈંટ માટે, લંબાઈ l = 22.5 સેમી; પહોળાઈ b = 7.5 સેમી અને ઊંચાઈ h = 6.5 સેમી
1 ઈંટનું ઘનફળ = lbh
= 22.5 × 7.5 × 6.5 સેમી³
= 1096.875 સેમી³
ઈંટ તેના \(\frac{1}{17}\) ઘનફળ જેટલું પાણી શોષી લે છે.
આથી ઈંટ દ્વારા તેના ઘનફળના \(\frac{16}{17}\) ભાગ જેટલું પાણી ખસેડવામાં આવે છે.
∴ 1 ઈંટ દ્વારા ખસેડાતા પાણીનું ઘનફળ = (\(\frac{16}{17}\) × 91096.875) સેમી³
ધારો કે, પાણી બહાર ન આવે તે રીતે ટાંકીમાં ઈંટો નાખી શકાય.
∴ n ઈંટો દ્વારા ખસેડાતા પાણીનું ઘનફળ = ખસતા પાણી દ્વારા ભરવાનો બાકી રહેતા ટાંકીના ભાગનું ઘનફળ
∴ n × \(\frac{16}{17}\) × 1096.875 = 1850400
∴ n = \(\frac{1850400 \times 17}{16 \times 1096.875}\)
∴ n = 1792.41
∴ n = 1792 (પૂર્ણકમાં)
આમ, પાણી બહાર ન આવે તે રીતે તે ટાંકીમાં 1792 ઈંટો નાખી શકાય.

પ્રશ્ન 4.
આપેલા મહિનાના કોઈ એક પખવાડિયામાં એક નદીની ઘાટીમાં 10 સેમી વરસાદ પડ્યો છે. જો તે ઘાટીનું ક્ષેત્રફળ 7280 કિમી² હોય, તો બતાવો કે કુલ વરસાદ લગભગ ત્રણ નદીઓના સામાન્ય પાણીના સરવાળા બરાબર હતો. પ્રત્યેક નદી 1072 કિમી લાંબી, 75 મીટર પહોળી અને 3 મીટર ઊંડી છે.
ઉત્તર:
1 કિમી² = 1000000 મી².
એક પખવાડિયામાં નદીની ઘાટીમાં પડેલા વરસાદના પાણીનું કુલ ઘનફળ = ઘાટીનું ક્ષેત્રફળ × પડેલ વરસાદની ઊંચાઈ
= 7280 કિમી² × 10 સેમી²
= 7280000000 મી² × 0.1 મી
= 728000000 મી³
= 0.728 કિમી³ ……………… (1)
એક નદીમાં રહેતા સામાન્ય પાણીનું ઘનફળ = 1072 કિમી × 75 મી × 3 મી
= 1072000 મી × 75 મી × 3 મી
= 241200000 મી³
∴ ત્રણ નદીમાં રહેતા સામાન્ય પાણીનું કુલ ઘનફળ = 3 × 241200000 મી³
= 723600000 મી³
= 0.7236 કિમી³ ……………….(2)
(1) અને (2)માં મેળવેલ કિંમતો લગભગ સમાન છે.
આમ, એક પખવાડિયામાં નદીની ઘાટીમાં પડેલ વરસાદનું પાણી છે
લગભગ ત્રણ નદીઓના સામાન્ય પાણીના સરવાળા બરાબર હતો.

પ્રશ્ન 5.
પતરાની એક ચીમની 10 સેમી લાંબા નળાકારના છેડે શંકુના આડછેદથી બનેલી છે. જો તેની કુલ ઊંચાઈ 22 સેમી હોય તથા નળાકાર ભાગનો 18 સેમી વ્યાસ 8 સેમી અને ચીમનીના ઉપરના ભાગનો વ્યાસ 18 સેમી હોય, તો ચીમની બનાવવામાં 22 સેમી? વપરાતા પતરાનું ક્ષેત્રફળ 10 સેમી શોધો. (જુઓ આકૃતિ)
ઉત્તર:

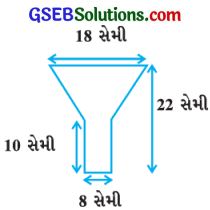
ચીમનીના નળાકાર ભાગ માટે, ત્રિજ્યા r = = \(\frac{8}{2}\) સેમી = 4 સેમી અને ઊંચાઈ h = 10 સેમી
નળાકાર ભાગની વક્ર સપાટીનું ક્ષેત્રફળ = 2πr h
= 2 × π × 4 × 10
= 80 π સેમી²
શંકુના આડછેદ માટે, મોટી ત્રિજ્યા r₁ = = \(\frac{18}{2}\) સેમી = 9 સેમી,
નાની ત્રિજ્યા r₂ = નળાકારની ત્રિજ્યા = 4 સેમી અને ઊંચાઈ h = 22 સેમી – 10 સેમી = 12 સેમી
શંકુના આડછેદની તિર્ધક ઊંચાઈ, l = \(\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
= \(\sqrt{12^{2}+(9-4)^{2}}\) સેમી
= \(\sqrt{144+25}\) સેમી
= \(\sqrt{169}\) સેમી = 13 સેમી
શંકુના આડછેદની વકસપાટીનું ક્ષેત્રફળ = πl (r₁ + r₂)
= π × 13 (9 + 4) સેમી²
= 169 π સેમી²
ચીમની બનાવવામાં વપરાતા પતરાનું ક્ષેત્રફળ = નળાકારની વક્રસપાટીનું ક્ષેત્રફળ + શંકુના આડછેદની વક્રસપાટીનું ક્ષેત્રફળ
= (80 π + 169 π) સેમી²
= 249 π સેમી²
= 249 x \(\frac{22}{7}\) સેમી²
= \(\frac{5478}{7}\) સેમી = 782\(\frac{4}{7}\) સેમી
આમ, ચીમની બનાવવામાં વપરાતા પતરાનું ક્ષેત્રફળ 782\(\frac{4}{7}\) સેમી છે.

પ્રશ્ન 6.
વિભાગ 13.5માં આપવામાં આવેલા સંકેતોની મદદથી શંકુના આડછેદની વકસપાટીનું ક્ષેત્રફળ અને કુલ પૃષ્ઠફળનું સૂત્ર તારવો.

પ્રશ્ન 7.
વિભાગ 13.5માં આપેલ સંકેતોની મદદથી શંકુના આડછેદનું ઘનફળ શોધવાનું સૂત્ર તારવો.
ઉત્તર:

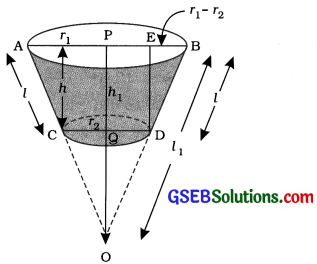
આપણે પ્રથમ ઘનફળ શોધવાનું સૂત્ર તારવીએ અને ત્યારબાદ વક્ર સપાટીનું ક્ષેત્રફળ તથા કુલ સપાટીનું ક્ષેત્રફળ શોધવાનાં સૂત્રો તારવીએ.
ધારો કે, શંકુના આડછેદ ACDB માટે ઊંચાઈ ૧, તિર્યક ઊંચાઈ l, મોટી ત્રિજ્યા r₁, અને નાની ત્રિજ્યા r₂ છે. આપણે તેની જોડે શંકુ OCD જોડી દઈએ.
આથી શંકુના આડછેદ ACDB એ OAB અને શંકુ OCDનો તફાવત છે.
ધારો કે, શંકુ OAB ની ઊંચાઈ ૧, અને તિર્યક ઊંચાઈ 1, છે, એટલે કે, OP = h₁; અને OA = OB = l₁.
તો, શંકુ OCDની ઊંચાઈ = OQ = h₁ – h.
હવે, ∆ OQD – ∆ OPB (ખૂબૂ શરત)

∴ h₁ = \(\frac{h r_{1}}{r_{1}-r_{2}}\) …………..(1)

હવે, શંકુ OCDની ઊંચાઈ = OQ
= h₁ – h
= \(\frac{h r_{1}}{r_{1}-r_{2}}\) – h
= \(\frac{h r_{2}}{r_{1}-r_{2}}\) ……………. (2)
શંકુના આડછેદનું ઘનફળ = શંકુ આABનું ઘનફળ – શંકુ OCDનું ઘનફળ
= \(\frac{1}{3}\) πr₁² h₁ – \(\frac{1}{3}\) π r₂² (h₁ – h)

= \(\frac{\pi}{3}\left[r_{1}^{2} \frac{h r_{1}}{r_{1}-r_{2}}-r_{2}^{2} \frac{h r_{2}}{r_{1}-r_{2}}\right]\) [(1) અને (2) પરથી)

= \(\frac{\pi h}{3}\left(\frac{r_{1}^{3}-r_{2}^{3}}{r_{1}-r_{2}}\right)\)

= \(=\frac{1}{3} \pi h\left(\frac{\left(r_{1}-r_{2}\right)\left(r_{1}^{2}+r_{1} r_{2}+r_{2}^{2}\right)}{r_{1}-r_{2}}\right)\)

= \(\frac{1}{3}\) πh (r₁² + r₂² + r₁r₂)

આમ, શંકુના આડછેદનું ઘનફળ = \(\frac{1}{3}\) πh (r₁² + r₂² + r₁r₂)
ધારો કે, r₁, ત્રિજ્યાવાળા વર્તુળનું ક્ષેત્રફળ = A₁ = πr₁² અને r₂ ત્રિજ્યાવાળા વર્તુળનું ક્ષેત્રફળ = A₂ = πr₂².

શંકુના આડછેદનું ઘનફળ = \(\frac{1}{3}\) πh (r₁² + r₂² + r₁r₂)

= \(\frac{h}{3}\left(\pi r_{1}^{2}+\pi r_{2}^{2}+\sqrt{\pi r_{1}^{2}} \cdot \sqrt{\pi r^{2}}\right)\)

= \(\frac{h}{3}\left(\mathrm{~A}_{1}+\mathrm{A}_{2}+\sqrt{\mathrm{A}_{1} \mathrm{~A}_{2}}\right)\)

વળી, ∆ DEBમાંથી, l = \(\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
હવે, ∆ OOD ~ ∆ OPB (ખૂબૂ શરત)

આથી, l₁ – l = \(\frac{l r_{1}}{r_{1}-r_{2}}-l=\frac{l r_{2}}{r_{1}-r_{2}}\) ……………(4)
શંકુના આડછેદની વક્ર સપાટીનું ક્ષેત્રફળ = શંકુ આABની વસપાટીનું ક્ષેત્રફળ – શંકુ OCDની વક્રસપાટીનું ક્ષેત્રફળ
= πr₁ l₁ – πr₂ l₂ (l₁ – l)
= πl \(\left(\frac{r_{1}{ }^{2}}{r_{1}-r_{2}}-\frac{r_{2}{ }^{2}}{r_{1}-r_{2}}\right)\) [(3) અને (4) પરથી]

= πl \(\left(\frac{r_{1}^{2}-r_{2}^{2}}{r_{1}-r_{2}}\right)\)

= πl (r₁ + r₂)

આમ, શંકુની વક્રસપાટીનું ક્ષેત્રફળ = πl (r₁ + r₂) જ્યાં, l = \(\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
આથી શંકુના આડછેદની કુલ સપાટીનું ક્ષેત્રફળ = πl (r₁ + r₂) + πr₁² + πr₂²