GSEB Solutions Class 10 Maths Chapter 2 Polynomials Ex 2.2

Gujarat Board GSEB Solutions Class 10 Maths Chapter 2 Polynomials Ex 2.2 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 2 Polynomials Ex 2.2

Question 1.
Find the zeroes of the following polynomial and verify the relationship between the zeroes and the coefficients

1. x² – 2x – 8
2. 4s² – 4s + 1
3. 6x³ – 3 – 7x
4. 4u² + 8u
5. t² – 15
6. 3x² – x – 4

Solution:
1. p(x) = x² – 2x – 8
= x² – 4x + 2x – 8
[By splitting middle term]
= x(x – 4) + 2(x – 4)
= (x – 4) (x + 2)
For zeroes of p(x),
p(x) = 0
⇒ (x – 4) (x + 2) = 0
⇒ x – 4 = 0
or x + 2 = 0
⇒ x = 4
or x = -2
⇒ x = 4, – 2.
Zeroes of p(x) are 4 and -2.
⇒ α = 4, β = -2

Verification of relationship between zeroes and coefficient:
Sum of the zeroes = 4 + (-2) = 2
⇒ α + β = 2
and \(\frac{-b}{a}=\frac{-(\text { coefficient of } x)}{\text { coefficient of } x^{2}}\)
= \(\frac{-(-2)}{1}\) = 2
⇒ α + β = \(\frac{-b}{a}\)
Product of the zeroes
αβ = 4 × (-2) = -8
and \(\frac{c}{a}=\frac{\text { constant term }}{\text { coefficient of } x^{2}}\)
= \(\frac{-8}{1}\) = -8
⇒ αβ = \(\frac{c}{a}\)

2. p(s) = 4s² – 4s + 1
= 4s² – 2s – 2s + 1
[By splitting middle term]
= 2s(2s – 1) – 1 (2s – 1)
(2s – 1) (2s – 1)
For zeroes of p(s),
P(s) = 0
⇒ (2s – 1) (2s – 1) = 0
⇒ 2s – 1 = 0
or 2s – 1 = 0

⇒ s = \(\frac{1}{2}\)
or s = \(\frac{1}{2}\)
⇒ s = \(\frac{1}{2}\), \(\frac{1}{2}\)
⇒ zeroes of p(s) are \(\frac{1}{2}\), \(\frac{1}{2}\)
⇒ α = \(\frac{1}{2}\), β = \(\frac{1}{2}\)
Verification of relationship between zeroes and coefficients:
Sum of the zeroes = \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1
⇒ α + β = 1

3. p(x) = 6x² – 3 – 7x
p(x) = 6x² – 7x – 3
= 6x² – 9x + 2x – 3
= 3x(2x – 3) + 1(2x – 3)
= (2x – 3) (3x + 1)
For zeroes p(x) = 0
⇒ (2x – 3) (3x + 1) = 0
⇒ 2x – 3 = 0
or 3x + 1 = 0

⇒ x = \(\frac{3}{2}\)
or x = \(\frac{-1}{3}\)
x = \(\frac{3}{2}\), \(\frac{-1}{3}\)
⇒ α = \(\frac{3}{2}\), β = \(\frac{-1}{3}\)
Now, verification of relationship between zeroes and coefficients.
Sum of the zeroes

Also, product of the zeroes;

4. p(u) = 4u² + 8 u
p(u) = 4u (u + 2)
For zeroes, p(u) = 0
⇒ 4 u(u + 2) = 0
⇒ u(u + 2) = 0
⇒ u = 0
or u + 2 = 0
⇒ u = 0
⇒ u = -2
So, zeroes of p(u) are 0 and -2.
⇒ α = 0, β = -2
Verification of relationship between zeroes and coefficients:
Sum of the zeroes,
α + β = 0 + (-2) = -2

5. t² – 15
P(t) = t² – 15
For zeroes p(t) = 0
t² – 15 = 0
t² – (\(\sqrt { 15 } \))² = 0
(t – \(\sqrt { 15 } \)) (t + \(\sqrt { 15 } \)) = o
⇒ t – \(\sqrt { 15 } \) = 0
or t + \(\sqrt { 15 } \) = 0
⇒ t = \(\sqrt { 15 } \)
t = –\(\sqrt { 15 } \)
So, zeroes of p(t) are \(\sqrt { 15 } \) and –\(\sqrt { 15 } \)
⇒ α = \(\sqrt { 15 } \), β = –\(\sqrt { 15 } \)
Verification of relationship between zeroes
and coefficients:
Sum of the zeroes,
α + β = \(\sqrt { 15 } \) + (-\(\sqrt { 15 } \)) = 0

6. p(x) = 3x² – x – 4
p(x) = 3x² – 4x + 3x – 4
= x(3x – 4) + 1(3x – 4)
= (3x – 4) (x + 1)
For zeroes, p(x) = 0
⇒ (3x – 4)(x + 1) = 0
⇒ 3x – 4 = 0
or x + 1 = 0
⇒ x = \(\frac{4}{3}\)
or x = -1
⇒ Zeroes of p(x) are \(\frac{4}{3}\) and -1.
⇒ α = \(\frac{4}{3}\), β = -1
Verification of relationship between zeroes and coefficients:
Now sum of the zeroes,

Question 2.
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.

1. \(\frac{1}{4}\), -1
2. \(\sqrt { 2 } \), \(\frac{1}{3}\)
3. 0, \(\sqrt { 5 } \)
4. 1, 1
5. \(\frac{-1}{4}\), \(\frac{1}{4}\)
6. 4, 1

Solution:
1. A quadratic polynomial, when the sum and product of its zeroes are given, is
p(x) = K [x² – (sum of the zeroes) x + Product of zeroes]
where K is constant.
Now sum of the zeroes = \(\frac{1}{4}\)
Product of the zeroes = -1
∴ Required quadratic polynomial is given

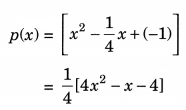
or K[4x² – x – 4]

2. \(\sqrt { 2 } \), \(\frac{1}{3}\)
Sum of the zeroes, S = \(\sqrt { 2 } \)
Product of the zeroes, P = \(\frac{1}{3}\)
∴ Required polynomial is
p(x) = K[x² – Sx + P]

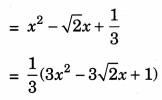
3. 0, \(\sqrt { 5 } \)
Sum of the zeroes S = 0
Product of the zeroes, P = \(\sqrt { 5 } \)
∴ Required polynomial is
p(x) = K[x² – Sx + P]
= x² – 0x + \(\sqrt { 5 } \)
p(x) = x² + \(\sqrt { 5 } \)

4. 1, 1
Sum of the polynomial, S = 1
Product of the polynomial, P = 1
∴ Required polynomial is
p(x) = K[x² – Sx + P]
= x² – 1x + 1
p(x) = x² – x + 1

5. \(\frac{-1}{4}\), \(\frac{1}{4}\)
Sum of the zeroes, S = \(\frac{-1}{4}\)
Product of the zeroes, P = \(\frac{1}{4}\)
∴ Required polynomial is
p(x) = K[x² – Sx + P]

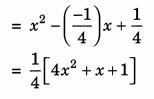
6. 4, 1
Sum of the zeroes, S = 4
Product of the zeroes, P = 1
∴ Required polynomial is
p(x) = K[x² – Sx + P]
p(x) = x² – 4x + 1