Gujarat Board GSEB Solutions Class 10 Maths Chapter 2 Polynomials Ex 2.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 2 Polynomials Ex 2.3
Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
- p(x) = x3 – 3x2 + 5x – 3; g(x) = x2 – 2
- p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
- p(x) = x4 – 5x + 6, g(x) = 2 – x2
Solution:
1. By applying the division algorithm to the given polynomials p(x) and g(x)

∴ Remainder = 7x – 9
degree of 7x – 9 = 1 < degree of (x2 – 2) = 2.
⇒ Quotient = x – 3
Remainder = 7x – 9
Verify: Quotient × Division + Remainder
= (x – 3) (x2 – 2) + (7x – 9)
= x3 – 2x – 3x2 + 6 + 7x – 9
= x3 – 3x2 + 5x – 3 = Dividend.
![]()
2. p(x) = x4 – 3x2 + 4x + 5
g(x) = x2 + 1 – x
Standard form of g(x) = x2 – x + 1.
Now, by applying the division algorithm to the given polynomials p(x) and g(x)

degree of 8 = 0 < degree of x2 – x + 1 = 2
So, Quotient = x2 + x – 3
Remainder = 8.
Verify: Quotient × Divisor + Remainder
= (x2 + x – 3) (x2 – x + 1) + 8
= x4 – x3 + x2 + x3 – x2 + x – 3x2 + 3x – 3 + 8
= x4 – 3x2 + 4x + 5
= Dividend
3. p(x) = x4 – 5x + 6
g(x) = 2 – x2
Standard form of g(x) = -x2 + 2
Now, by applying division algorithm to the given polynomial p(x) and g(x).

∵ deg. of -5x + 10 = 1 < deg. of -x2 + 2 = 2
So, Quotient = -x2 – 2
Remainder = -5x + 10.
Verify: Quotient × Divisor + Remainder
= (-x2 – 2) × (-x2 + 2) + (-5x + 10)
= (-x2)2 – 4 – 5x + 10
= x4 – 5x + 6 = Dividend
![]()
Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
- t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12
- x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
- x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
Solution:
By applying division algorithm to the given polynomials,

Since, the remainder is 0, hence the first polynomial is a factor of the second polynomial.
2. x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
By applying division algorithm to the given polynomials,

Since the remainder is 0, hence the first polynomial is a factor of the second polynomial.
![]()
3. x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
By applying division algorithm to the given polynomials,

Since the remainder is 2 (≠0), hence the first polynomial is not a factor of second polynomial.
Question 3.
Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two zeroes are and \(\sqrt{\frac{5}{3}}\) and –\(\sqrt{\frac{5}{3}}\).
Solution:
Since two zeroes are \(\sqrt{\frac{5}{3}}\) and –\(\sqrt{\frac{5}{3}}\) hence
\(\left(x-\sqrt{\frac{5}{3}}\right)\left(x+\sqrt{\frac{5}{3}}\right)=x^{2}-\frac{5}{3}\) is a factor of the given polynomial.
Now, we divide the given polynomial by x2 – \(\frac{5}{3}\).
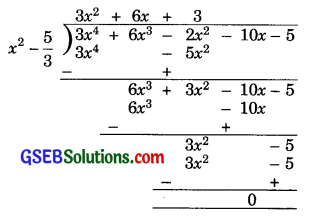
So, 3x4 + 6x3 – 2x2 – 10x – 5
= [x2 – \(\frac{5}{3}\)] (3x2 + 6x + 3)
Now, 3x2 + 6x + 3
= 3x2 + 3x + 3x + 3
= 3x(x + 1) + 3(x + 1)
= 3(x + 1) (x + 1)
So, its zeroes are -1 and -1.
⇒ Remaining two zeroes of the given polynomial are -1 and -1.
![]()
Question 4.
On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and -2x + 4, respectively. Find g(x).
Solution:
p(x) = x3 – 3x2 + x + 2
q(x) = x – 2
r(x) = -2x + 4
By division algorithm for polynomials
p(x) = g(x) × q(x) + r(x)
⇒ x3 – 3x2 + x + 2
= (x – 2) g(x) + (-2x + 4)
⇒ (x – 2) g(x)
= x3 – 3x2 + x + 2 + 2x – 4
= x3 – 3x2 + 3x – 2
∴ g(x) = (x3 – 3x2 + 3x – 2) ÷ (x – 2)

∴ g(x) = x2 – x + 1
![]()
Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
- deg p(x) = deg q(x)
- deg q(x) = deg r(x)
- deg r(x) =0.
Solution:
1. deg p(x) = deg q(x)
Let p(x) = 8x2 – 8x + 16
and g(x) = 8
∴ q(x) = x2 – x + 2
r(x) = 0
p(x) = g(x) × q(x) + r(x)
![]()
2. deg q(x) = deg r(x)
Let p(x) = x3 + x2 + x + 1
and g(x) = x2 – 1
∴ q(x) = x + 1
r(x) = 2x + 2
p(x) = g(x) × q(x) + r(x)
3. deg r(x) = 0
Let p(x) = x4 + x3 + x2 – 2x – 3
and g(x) = x2 – 2
∴ q(x) = x2 + x + 3
r(x) = 3
p(x) = g(x) × q(x) + r(x)