Gujarat Board GSEB Solutions Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
Question 1.
Solve the following pairs of equations by reducing them to a pair of linear equations:
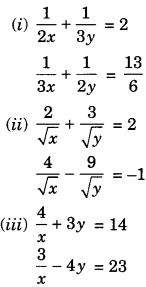

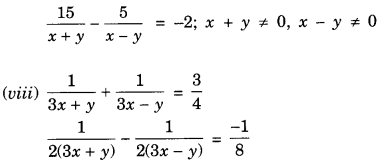
Solution:
(i) The given pair of equations is
\(\frac { 1 }{ 2x } +\frac { 1 }{ 3y } =2\) …………… (1)
\(\frac { 1 }{ 3x } +\frac { 1 }{ 2y } =\frac { 13 }{ 6 } \) ………….. (2)
Put \(\frac { 1 }{ x } =a\) …………………. (3)
and \(\frac { 1 }{ y } =b\) ……………… (4)
Then the equations (1) and (2) can be rewritten as
\(\frac { 1 }{ 2 } a+\frac { 1 }{ 3 } b=2\) ………………… (5)
\(\frac { 1 }{ 3 } a+\frac { 1 }{ 2 } b=\frac { 13 }{ 6 } \) ………….. (6)
3a + 2b = 12 ………….. (7)
2a + 3b = 13 …………….. (8)
Multiplying equations (7) by 3 and equation (8) by 2, we get
9a + 6b = 36 …………… (9)
4a + 6b = 26 ………….. (10)
Subtracting equation (10) from equation (9), we get
5a = 10
a = \(\frac { 10 }{ 5 } =2\) ………………. (11)
Substituting this”value of a in equation (9), we get
9(2) + 6b = 36
18 + 6b = 36
6b = 36 – 18 = 18
b = \(\frac { 18 }{ 6 }\) = 3 …………….. (12)
From equation (3) and equation (11), we get
\(\frac { 1 }{ x }\) = 2
x = \(\frac { 1 }{ 2 }\)
From equation (4) and equation (11), we get
\(\frac { 1 }{ y }\) = 3
x = \(\frac { 1 }{ 3 }\)
Hence, the solution of the given pair of equations is
x = \(\frac { 1 }{ 2 }\), y = \(\frac { 1 }{ 3 }\)
Verification: Substituting x = \(\frac { 1 }{ 2 }\), y = \(\frac { 1 }{ 3 }\), we find that both the equations (1) and (2) are satisfied as shown below:

Hence, the solution we have got is correct.
(ii) The given pair of equations is

Then equations (1) and (2) can be rewritten as
2u + 3υ = 2 ……………. (5) υ u
4u – 9υ = – 1 …………… (6)
MultipLying equation (5) by 3, we get
6u + 9υ = 6 …………….(7)
Adding equation (6) and equation (7), we get
10u = 5
u = \(\frac { 5 }{ 10 }\) = \(\frac { 1 }{ 2 }\) ………… (8)
Substituting the value of u in equation (5), we get
\(\left( \frac { 1 }{ 2 } \right)\) = 3υ = 2
1 + 3υ = 2
3υ = 2 – 1 = 1 …………… (9)
υ = \(\frac { 1 }{ 3 }\)
From equation (3) and equation (8), we get
\(\frac { 1 }{ \sqrt { x } } \) = \(\frac { 1 }{ 2 }\)
\(\sqrt { x }\) = 2
x = 4
From equation (4) and equation (9), we get
\(\frac { 1 }{ \sqrt { y } } \) = \(\frac { 1 }{ 3 }\)
\(\sqrt { y }\) = 3
y = 9
Hence, the solution of the given pair of equation is x = 4, y = 9.
Verification: Substituting x = 4, y = 9,
we find that both the equations (1) and (2) are satisfied as shown below:

Hence, the solution we have got is correct.
![]()
(iii) \(\frac { 4 }{ x }\) + 3y = 14 ………….. (1)
\(\frac { 3 }{ x }\) – 4y = 23 …………….. (2)
Put \(\frac { 1 }{ x }\) = X
The equation (1) and (2) can be written as
4X + 3y = 14 ……………..(4)
3X – 4y = 23 ………………(5)
From equation (5),
4y = 3X – 23
\(y=\frac { 3X-23 }{ 4 } \)
Substitute this value ofy in equation (4), we get
\(4X+3\left( \frac { 3X-23 }{ 4 } \right) =14\)
16X + 9X – 69 = 56
25X = 56 + 69 = 125
X = \(\frac { 125 }{ 25 }\) = 5 ………….. (7)
Substituting this value of X in equation (6), we get
\(y=\frac { 3(5)-23 }{ 4 } =\frac { 15-23 }{ 4 } \)
= \(\frac { – 8 }{ 4 }\) = – 2 ……………….. (8)
From equation (3) and equation (7), we get
\(\frac { 1 }{ x }\) = 5
x = \(\frac { 1 }{ 5 }\) ……….(9)
Hence, the solution of the given pair of
equations is x = \(\frac { 1 }{ 5 }\), y = – 2.
Verification: Substituting x = \(\frac { 1 }{ 5 }\), y = – 2,
we find that both the equations (1) and (2)
are satisfied as shown below:

Hence, the solution is correct.
(iv) The given pair of equations is
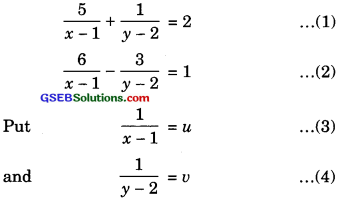
Then equations (1) and (2) can be written as
5u + υ = 2 ……………..(5)
6u – 3υ = 1 ……………(6)
Multiplying equation (5) by 3, we get
15u + 3υ = 6
Adding equation (6) and equation (7), we get
21u + 7
u = \(\frac { 7 }{ 21 }\) = \(\frac { 1 }{ 3 }\) ………….. (8)
Substituting this value of u in equation (5), we get

From equation (3) and equation (s), we get
\(\frac { 1 }{ x-1 } \) = \(\frac { 1 }{ 3 }\)
x – 1 = 3
x = 1+ 3 = 4
From equation (4) and equation (9), we get
\(\frac { 1 }{ y-2 } \) = \(\frac { 1 }{ 3 }\)
y – 2 = 3
y = 3 + 2 = 5
Hence, the solution of the given pair of
equations is x = 4, y = 5.
Verification: Substituting x = 4, y = 5, we
find that both the equations (1) and (2) are
satisfied as shown below:
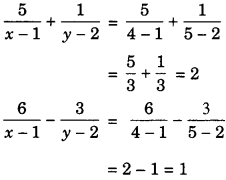
Hence, the solution is correct.
(v) The given pair of equations is

Then the equations (3) and (4) can be rewritten as
7υ – 2u = 5
8υ + 7u = 15
7υ – 2u – 5 = 0
8υ + 7u – 15 = 0
To solve the equations by the cross multiplication method, we draw the diagram below:

From equation (5) and equation (10), we get
\(\frac { 1 }{ x }\) = 1
x = 1
From equation (6) and equation (9), we get
\(\frac { 1 }{ y }\) = 1
y = 1
Hence, the solution of the given pair of
equations is x = 1, y = 1.
Verification: Substituting x = 1, y = 1 we
find that both the equations (1) and (2) are satisfied as shown below:
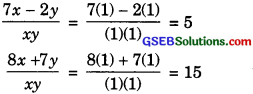
Hence, the solution is correct.
(vi) The given pair of equations is
6x + 3y = 6xy
2x + 4y = 5xy
(Dividing throughout by xy)

Then equations (1) and (2) can be rewritten as
6υ + 3u = 6
2υ + 4u = 5
Multiplying equation (6) by 3, we get
6υ + 12u = 15
Subtracting equation (5) from equation (7), we get
9u = 9
u = \(\frac { 9 }{ 9 }\) = 1
\(\frac { 1 }{ x }\) = 1
x = 1 [ using (3)]
Substituting this value of u in equation (5), we get
6u + 3 x 1 = 6
6υ + 3 = 6
6υ = 6 – 3 = 3
υ = \(\frac { 3 }{ 6 }\) = \(\frac { 1 }{ 2 }\)
\(\frac { 1 }{ y }\) = \(\frac { 1 }{ 2 }\)
y = 2 [ using (4)]
Hence, the solution of the given pair of equations is x = 1, y = 2.
Verification: Substituting x = 1, y = 2, we
find that both the equations (1) and (2) are satisfied as shown below:
\(\frac { 6 }{ y }\) + \(\frac { 3 }{ x }\) = \(\frac { 6 }{ 2 }\) + \(\frac { 3 }{ 1 }\)
= 3 + 3 = 6
\(\frac { 2 }{ y }\) + \(\frac { 4 }{ x }\) = \(\frac { 2 }{ 2 }\) + \(\frac { 4 }{ 1 }\)
= 1+ 4 = 5
Hence, the solution is correct.
(vii) The given pair of equations is

Then equations (1) and (2) can be written as
10u + 2υ = 4 ………….(5)
15u – 5υ = – 2 ………….. (6)
Dividing (5) throughout by 2, we have
5u + υ = 2 ………… (7)
Multiplying equation (7) by 3, we get
15u + 3υ = 6 ………..(8)
Subtracting equation (6) from equation (8), we get
8υ = 8
υ = \(\frac { 8 }{ 8 }\) = 1 …………….(9)
Substituting this value of u in equation (7), we get
Su + 1=2
Substituting this value of u in equation (7), we get
5u + 1 = 2
5u = 2 – 1 = 1
u = \(\frac { 1 }{ 5 }\) ………………..(10)
From equation (3) and equation (10), we get
\(\frac { 1 }{ x+y } \) = \(\frac { 1 }{ 5 }\)
= x + y = 5 ………………(11)
From equation (4) and equation (9), we get
\(\frac { 1 }{ x-y } \) = 1
x – y = 1 ……………… (12)
Adding equation (11) and equation (12), we get
2x = 6
x = \(\frac { 6 }{ 2 }\) = 3
Substitute this value of x in equation (11), we get
3 + y = 5
y = 5 – 3 = 2
Hence, the solution of the given pair of equations is x = 3, y = 2.
Verification: Substituting x = 3, y = 2,
we find that both the equations (1) and (2) are satisfied as shown below:

Hence, the solution is correct.
(viii) The given pair of equations is
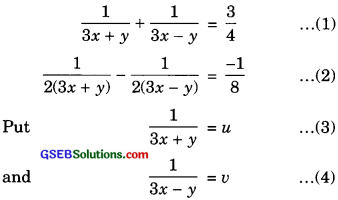
Then equation (1) and (2) can be rewritten as
u + υ = \(\frac { 3 }{ 4 }\) ……………. (5)
\(\frac { 1 }{ 2 }\) u – \(\frac { 1 }{ 2 }\) υ = – \(\frac { 1 }{ 8 }\) ………….. (6)
(Multiplying both sides of(6) by 2) gives
u – υ = – \(\frac { 1 }{ 4 }\) …………… (7)
Adding equation (5) and equation (7), we get
2u = \(\frac { 3 }{ 4 }\) – \(\frac { 1 }{ 4 }\) = \(\frac { 1 }{ 2 }\)
u = \(\frac { 1 }{ 4 }\) …………… (8)
Subtracting equation (7) from equation (5), we get
2υ = \(\frac { 3 }{ 4 }\) + \(\frac { 1 }{ 4 }\) = 1
υ = \(\frac { 1 }{ 2 }\) …………… (9)
From equation (3) and equation (8), we get
\(\frac { 1 }{ 3x+y }\) = \(\frac { 1 }{ 4 }\)
3x + y = 4
From equation (4) and equaation (9), We gete
\(\frac { 1 }{ 3x-y }\) = \(\frac { 1 }{ 2 }\)
3x – y = 2
Adding equation (10) and equation (11), we get
6x = 6
x = \(\frac { 6 }{ 6 }\) = 1
Substituting this value of x in equation (10), we get
3(1) + y = 4
3 + y = 4
y = 4 – 3 = 1
Hence, the solution of the given pair of
equations is x = 1, y = 1.
Verification: Substituting x = 1, y = 1,
we find that both the equations (1) and (2) are satisfied as shown below:

Hence, the solution is correct.
![]()
Question 2.
Formulate the following problems as a pair of equations, and hence find their solutions:
(i) Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
(ii) 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
(iii) Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Solution:
(i) Let her speed of rowing in still water be x kim/hour and the speed of the current be y km/hour.
Then, her speed of rowing downstream
= (x + y) km/hour
and, her speed of rowing upstream
= (x – y) km/hour
Also, ![]()
In the first case, when she goes 20 km
downstream, the time taken is 2 hours.
∴\(\frac { 20 }{ x+y }\)
= x + y = 10
In the second case, when she goes 4 km
upstream, the time taken is 2 hours.
∴\(\frac { 4 }{ x-y }\)
= x – y = 2 …………….(2)
Adding equation (1) and equation (2), we get
2x = 12
x = \(\frac { 12 }{ 2 }\) = 6
Substituting this value of x in equation (1), we get
6 + y = 10
y = 10 – 6 = 4
Hence, the speed of her rowing in still water
is 6 km/hour and the speed of the current is 4 km/hour.
Verification: Substituting x = 6, y = 4, we
find that both the equations (1) and (2) are
satisfied as shown below:
x + y = 6 + 4 = 10
x – y = 6 – 4 = 2
Hence, the solution is correct.
![]()
(ii) Let the time taken by 1 woman alone to finish the embroidery work be x days and the time taken by 1 man alone to finish the embroidery be y days.
Then
1 woman’s 1 day’s work = \(\frac { 1 }{ x }\)
and 1 man’s 1 day’s work = \(\frac { 1 }{ y }\)
∴ 2 womens 1 day’s work= \(\frac { 2 }{ x }\)
and 5 men’s 1 day’s work = \(\frac { 5 }{ y }\)
2 women and 5 men can ‘togethcr finish one embroidery work in 4 days.
∴\(4=\left( \frac { 2 }{ x } +\frac { 5 }{ y } \right) =1\)
\(\frac { 2 }{ x }\) + \(\frac { 5 }{ y }\) = \(\frac { 1 }{ 4 }\) …………….. (1)
Again, 3 women’s 1 day’s work = \(\frac { 3 }{ x }\)
and 6 men’s 1 day’s work = \(\frac { 6 }{ y }\)
3 women and 6 men can together finish one embroidery work in 3 days.
\(3=\left( \frac { 3 }{ x } +\frac { 6 }{ y } \right) =1\)
\(\frac { 3 }{ x }\) + \(\frac { 6 }{ y }\) = \(\frac { 1 }{ 3 }\) ………….. (2)
Put \(\frac { 1 }{ x }\) = u …………… (3)
Put \(\frac { 1 }{ y }\) = υ ………………….. (4)
Then equations (1) and (2) can be rewritten as
2u + 5υ = \(\frac { 1 }{ 4 }\) ……………… (5)
3u + 6υ = \(\frac { 1 }{ 3 }\) …………….. (6)
Multiplying equation (5) by 3 and equation (6) by 2, we get
6u + 15υ = \(\frac { 3 }{ 4 }\) …………… (7)
6u + 12υ = \(\frac { 2 }{ 3 }\) ………….. (8)
Subtracting equation (8) from equation (7), we get
3υ = \(\frac { 3 }{ 4 }\) – \(\frac { 2 }{ 3 }\) = \(\frac { 1 }{ 12 }\)
υ = \(\frac { 1 }{ 36 }\) ………………… (9)
Substituting this value of y in equation (5), we get
2u + \(5\left( \frac { 1 }{ 36 } \right)\) = \(\frac { 1 }{ 4 }\)
2u + \(\frac { 5 }{ 36 }\) = \(\frac { 1 }{ 4 }\)
2u = \(\frac { 1 }{ 4 }\) – \(\frac { 5 }{ 36 }\)
2u = \(\frac { 9 }{ 36 }\) – \(\frac { 5 }{ 36 }\)
2u = \(\frac { 4 }{ 36 }\) = \(\frac { 1 }{ 9 }\)
u = \(\frac { 1 }{ 18 }\) ………….. (10)
From equation (3) and equation (10), we get
\(\frac { 1 }{ x }\) = \(\frac { 1 }{ 18 }\)
x = 18
From equation (4) and equation (9), we get
\(\frac { 1 }{ y }\) = \(\frac { 1 }{ 36 }\)
y = 36
Hence, the time taken by 1 woman alone to finish the embroidery work is 18 days and the time taken by 1 man alone to finish the embroidery work is 36 days.
Verification : Substituting x = 18, y = 36,
we find that both the equations (1) and (2) are satisfied as shown below:

(iii) Let the speed of the train and the bus be x km/hour and y km/hour respectively.
When she travels 60 km by train and the remaining (300 – 60) km, i.e., 240 km by bus, the time taken is 4 hours.
∴\(\frac { 60 }{ x }\) + \(\frac { 240 }{ y }\) = 4
![]()
Dividing throughout by 60,
\(\frac { 1 }{ x }\) + \(\frac { 4 }{ y }\) = \(\frac { 1 }{ 15 }\)
When she travels loo km by train and the remaining (300 – 100) km, i.e., 200 km by bus, the time taken is 4 hours 10 minutes, i.e., \(\frac { 25 }{ 6 }\) hours.
∴\(\frac { 100 }{ x }\) + \(\frac { 200 }{ y }\) = \(\frac { 25 }{ 6 }\)
Dividing throughout by 25,
\(\frac { 4 }{ x }\) + \(\frac { 8 }{ y }\) = \(\frac { 1 }{ 6 }\) ……………… (2)
Multiplying (1) by 2, we get
\(\frac { 2 }{ x }\) + \(\frac { 8 }{ y }\) = \(\frac { 1 }{ 6 }\) ………….. (3)
Subtracting equation (3) from equation (2), we get
\(\frac { 2 }{ x }\) = \(\frac { 1 }{ 6 }\) – \(\frac { 2 }{ 15 }\) = \(\frac { 1 }{ 30 }\)
x = 60
Substituting this value of x in equation (3), we get
\(\frac { 2 }{ 60 }\) + \(\frac { 8 }{ y }\) = \(\frac { 2 }{ 15 }\)
\(\frac { 1 }{ 30}\) + \(\frac { 8 }{ y }\) = \(\frac { 2 }{ 15 }\)
\(\frac { 8 }{ y }\) = \(\frac { 2 }{ 15 }\) – \(\frac { 1 }{ 30 }\) = \(\frac { 1 }{ 10 }\)
y = 80
So, the solution of the equations (1) and (2)
is x = 60 and y = 80.
Hence, the speed of the train is 60 km/hour and the speed of the bus is 80 km/hour.
Verification: Substituting x= 60, y = 80,
we find that both the equations (1) and (2) are satisfied as shown below:
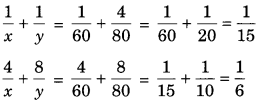
Hence, the solution is correct.
![]()