Gujarat Board GSEB Solutions Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
Question 1.
The ages of two friends Aol and Rijo differ by 3 years, Mi’s father Dharam is twice as old as Axil and Riju is twice as old as his aislar Cathy. The ages of Cathy and Pharam differ by 30 years. Find the ages of Ani and Biju.
Solution:
Let the age-s of Ani and Biju be x years and yea respectively- Then, according to the question,
x – y = ±3 ………………….(1)
Age of Ani’s father Dharam = ax years
Age of Biju’a sister = \(\frac { y }{ 2 } \) years
According to the question,
2x – \(\frac { y }{ 2 } \)
4x – y = 60 ……………… (2)
Case I: When x – y = 3
Then, we have
x – y = 3 ……………… (1)
4x – y = 60 ……………. (2)
Subtracting equation tI) from equation (2),
3x = 57
x = \(\frac { 57 }{ 3 } \) = 19 years
Substituting the value of x in equation (1),
19 – y = 3
Ani’s age = 19 years
Biju’s age = 16 years
Verification:
x – y = 19 – 16 – 3
4x – y = 4 x 19 – 16
= 76 – 16 = 60
This verifies the solution.
Case II: When x – y = – 3
Then, we have
x – y = – 3 ……………… (3)
4x – y = 60 ………… (2)
Subtracting equation (3) from equation (2), we get
3x = 63
x = \(\frac { 63 }{ 3 } \) = 21
Subetituting the value of x in the equation (3). we get
21 – y = – 3
y = 24
Ani’s age = 21 years
Bijus age = 24 years
verification:
x – y = 21 – 24 = – 3
4x – y = 4(21) – 24
= 84 – 24 = 60
This verifies the solution,
![]()
Question 2.
One says, “Give me a hundred, friend! I shall then becomes twice us nch as you”, The othcr replies. “1f you give me ten, I shall be six times as rich as you”. Tell mu what. is the amount of their (respcctive) capital.
[From the Bijaganita of Bhasknrn II]
[Hint : x+ 100 = 2(y – 100), y + 10 = 6 (x – 10)]
Solution:
Let the amounts of their respective capitals be
₹ x and ₹ y respectively.
Then, according to the question,
x + 100 = – 100
x – 2y = – 300 …………….. (1)
and 6(x – 10) = y + 10
6x – y = 70
From equatton (1),
x = 2y – 300
Substituting the value of x in equation (2), we get
6(2y – 300) – y = 70
12y – l800 – y = 70
11 y = 1870
y = \(\frac { 1870 }{ 11 } \) = 170
Substituting this value of y in equation (3), we get
x = 2 (170) – 300
= 340 – 300 = 40
So, the solution of the equations (1) and (2)
is x= 40 and y 170. Hence, the amount.s of
their respective capitals are ₹ 40 and ₹ 170 reapcetivcly.
Verification : Substituting z = 40, y = 170,
we find thai both the equations (1) and (2) are satisfied as shown below:
x – 2y = 40 – 2 (170)
= 40 – 340 = – 300
6x – y = 6(40) – 170
=240 – 170 = 70
Hence, the solution we have got is correct.
![]()
Question 3.
A tain covered a certain diietaswe at a uniform speed. 1f the tain would have been 10 km/h faster, it would have taken 2 hours lete than the scheduled tiene. And, if the tain were slower by 10 km/h; it would have taken 3 hours more than the schedulod tiene. Find the distance covered by the train.
Solution:
Let the artual speed 0f the train 6ex km/hour
and the actual time taken byy hours Then.
Distance = Speed x Tinte
Distante = (xy) km
According to the question.
xy = (x + 10) (y – 2)
xy = xy – 2x + 10y – 20
2x – 10 y + 20 = 0
x – 5y + 10 = 0 ……………… (1)
[Dividing throughout by 2]
and, xy = (x + 10) (y – 2)
xy = xy – 2x + 10y – 20
3x – 10y – 30 = 0
To solve the equations (1) and (2) by the cross
multiplication method, we draw the diagram below:

So, the solution of the equations (1) and (2) is x = 50 andy = 12.
Hence, the distance covered by the train is 50 x 12 = 600 km.
Verification: Substituting x = 50, y = 12,
we find that both the equations (1) and (2) are
satisfied as shown below.
x – 5y + 10 = 50 – 5(12) + 10
= 50 – 60+ 10 = 0
3x – 10y – 30 = 3(50) – 10(12) – 30
= 150 – 120 – 30
= 0
Hence, the solution is correct.
![]()
Question 4.
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
Solution.
Let the number of students in the class be x and the number of rows bey. Then, number of
students in each row = \(\frac { x }{ y } \)
According to the equation,
If 3 students are extra in row, then there would
be 1 row less, i.e., when each row has \(\left( \frac { x }{ y } +3 \right) \)
students, then the number of rows is (y – 1).
∴Total number of students = number of rows x number of students in each row
x = 1 + 3 (y – 1)
x = x – \(\frac { x }{ y } \) + 3y – 3
\(\frac { x }{ y } \) – 3y + 3 = 0 ………………. (1)
and, if 3 students are less in a row, then there would be 2 rows more, i.e., when each row has
\(\left( \frac { x }{ y } -3 \right) \) students, then the number of rows is
(y + 2)
∴Total number of students = Number of rows x Number of students in each row
x = \(\left( \frac { x }{ y } -3 \right) \)(y + 2)
x = x + \(\frac { 2x }{ y } \) – 3y – 6
\(\frac { 2x }{ y } \) – 3y – 6 = 0 …………… (2)
Put \(\frac { x }{ y } \) = u …………………..(3)
Then equations (1) and (2) can be rewritten as
u – 3y + 3 = 0
2u – 3y – 6 = 0
Subtracting equation (4) from equation (5), we
u – 9 = 0
u = 9 …………………… (6)
Substituting this vahe of u in equation (4), we get
9 – 3y +3 = 0
– 3y + 12 = 0
3y = 12
y = \(\frac { 12 }{ 3 } \) = 4
From equation (3) and equation (6), we get
\(\frac { x }{ y } \) = 9
\(\frac { x }{ 4 } \) = 9
Using (7)
So, the solution of the equations (1) and (2) is
x = 36 and y = 4. Hence, the number of students
in the class x = 36.
Verification: Substituting x = 36, y = 4, we
find that both the equations (1) and (2) are satisfied as shown below:
\(\frac { x }{ y } \) – 3y + 3 = \(\frac { 36 }{ 4 } \) – 3(4) + 3
= 9 – 12 + 3 = 0
\(\frac { 2x }{ y } \) – 3y – 6 = \(\frac { 2(36) }{ 4 } \) – 3(4) – 6
= 18 – 12 – 6 = 0
Hence, the anlution is correct.
![]()
Question 5.
In a ∆ABC, \(\angle C \) = 3 \(\angle B \) = 2 \(\left( \angle A+\angle B \right) \)Find the
three angles.
Solution.
We have
\(\angle C \) = 3 \(\angle B \) = 2 \(\left( \angle A+\angle B \right) \) ……… (1)
We know that the sum of the measurea of three
angles of a triangle is 180°.
∴\(\angle A \) + \(\angle B \) + \(\angle C \) = 180° ……………. (2)
(1) and (2) give
\(\angle A \) + \(\angle B \) + 2 \(\left( \angle A+\angle B \right) \) = 180° ……… (2)
3\(\angle A \) + 3\(\angle B \) = 180°
\(\angle A \) + \(\angle B \) = 60° ……………..(3)
(Dividing theought by 3)
and, \(\angle A \) + \(\angle B \) + 3\(\angle B \) = 180°
\(\angle A \) + 4 \(\angle B \) = 180°
Subtracting equation (3) from equation (4), we get
3\(\angle B \) = 120°
\(\angle B \) = \(\frac { 120° }{ 3 } \) = 40°
Substituting this value \(\angle B \) = 40 equation (3), we get
\(\angle A \) + 40° = 60°
\(\angle A \) = 60° – 40°
Again from(1)
\(\angle C \) = 3 \(\angle B \) = 3(40°) = 120°
Hence, the three angles of the ∆ABC are given by \(\angle A \) = 20°,\(\angle B \) = 40° and \(\angle C \) = 120°.
Verification: Substituting \(\angle A \) = 20°,\(\angle B \) = 40° and \(\angle C \) = 120°.
we find that (1) is satisfied as shown below:
\(\angle C \) = 3 \(\angle B \) = 2 \(\left( \angle A+\angle B \right) \)
120° = 3(40°) = 2( 20° + 40°)
Hence, the solution is correct
![]()
Question 6.
Draw the graphs of the equations 5x – y = 5 and 3x – y = 3, Determine lo co-ordinate of the vertices of the triangle formed by these lines end they-axis.
Solution:
The given equations are
5x – y = 5
3x – y = 3
Let us draw the graphs of equations (1) and (2) by finding two solutions of each of the equations.
These two solutions of each of the equation (1) and (2) are given beiow in taHe 1 and table 2 respectively,
For equation (1)
y = 5x – 5
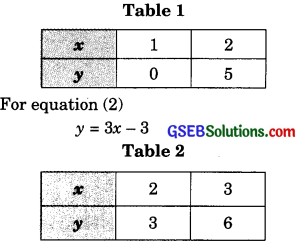
We plot the points A(1,0) and B(2, 5) on a graph pnpr and join these paints t0.
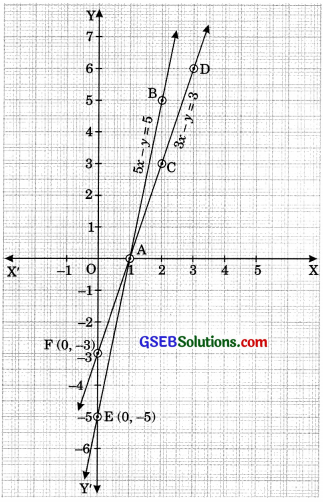
Form the line AB repreeenting the equation (1) aa ahown in the figure. Also, we plot the pointa C(2,3) and D(3, 6) on the same graph paper and join theae pointa to form the line CD representing the equation (2) ea ahown in the same figure.
In the figure, we aheerve that the coordinatea of the verticee of the triangle AEF are A(1,0), E(0,-5) and F(0,-3).
![]()
Question 7.
Solve the following pair of hnear equationa:

Solution:
(i) The gwee pelt of linear equatione
px + qy = p – q …………… (1)
qx – py = p + q ……………. (2)
Multiplying equation (1) hyp and equation (2) by q, we get
p2x + pqy = p3 – pq …………. (3)
q2x – pqy + q2 …………… (4)
Adding equation (3) and equation (4), we get
(p2 + q2)x = p2 + question
x = \(\frac { { p }^{ 2 }+{ q }^{ 2 } }{ { p }^{ 2 }+{ q }^{ 2 } } \) = 1
Subatituting this value ois in equation (1), we get
p(1) + qy = p – q
qy = – q
y = \(\frac { -q }{ q } \)
So. the solution of the given pair of linear equations is x = 1, y = -1.
VerifIcation Substituting x = 1, y = -1, we
find that both the equations (1) and (2) are satisfied as shown below:
px + qy = p(1) + q(-1)
= p – questionqx – py = q(1) – p(-1)
= q + p = p + q
Hence, the solution is correct.
(ii) The given pair of linear equations is
ax + by = c ……………… (1)
bx + ay = 1 + c …………. (2)
ax + by – c = 0 ……………….(3)
bx + ay – (1 + c) = 0 ……………. (4)
To solve the equations by the cross multiplication method, we draw the diagram below:
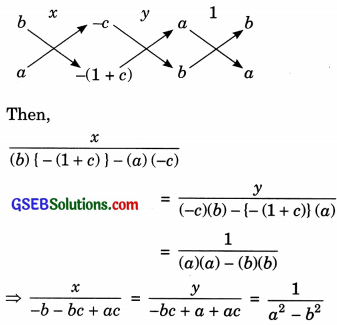
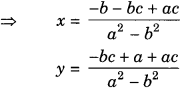
Hence, the solution of the given pair of linear equations is
![]()
Verification: Substatituting
![]()
we find that both the equations (1) and (2) are satisfied as shown below:

This verifies the solution.
(iii) The given pair of linear equations is
\(\frac { x }{ a } \) – \(\frac { y }{ b } \) = 0 ……………..(1)
ax + by = a2 + b2 ………….(2)
From equation (1),
\(\frac { y }{ b } \) = \(\frac { x }{ a } \)
y = \(\frac { b }{ a } \) x
Substituting the value of y in equation (2), we get
ax + b \(\left( \frac { b }{ a } x \right) \) = a2 + b2
\(\frac { { a }^{ 2 }+{ b }^{ 2 } }{ a } \) x = a2 + b2
x = \(\frac { a\left( { a }^{ 2 }+{ b }^{ 2 } \right) }{ { a }^{ 2 }+{ b }^{ 2 } } \)
Substituting this value of x in equation (3), we get
y = \(\frac { b }{ a } \) (a) = b
Hence, the solution of the given pair of
linear equations is x = a, y = b.
Verification: Substituting x = a, y = b, we
find that both the equations (1) and (2) are
satisfied as shown below:
\(\frac { x }{ a } \) – \(\frac { y }{ b } \) = \(\frac { a }{ a } \) – \(\frac { b }{ b } \)
= 1 – 1 = 0
ax + by = a (a) + b (b)
= a2 + b2
This verifies the solution.
(iv) The given pair of linear equations is
(a – b) x +(a + b) y = a2 – 2ab -b2
(a + b)(x + y) = a2 + b2
(a + b) x + (a + b) y = a2 + b2 ………….(2)
Subtracting equation (2) from equation (1), we get

Substituting this value of x in equation (1), we get
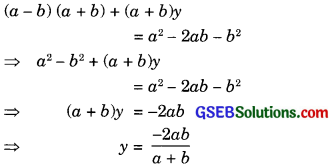
Hence, the solution of the given pair of linear equations is
x = a + b, y = \(\frac { -2ab }{ a+b } \)
Verification: Substituting x = a + b and y = \(\frac { -2ab }{ a+b } \) we find that both the equations (1) and (2) are satisfied as shown below:
(a – b) x + (a + b) y

This verifies the solution.
(v) The given pair of linear equations is
152x – 378y = – 74 ……………. (1)
– 378x + 152y = – 604 ……………. (2)
Adding equation (1) and equation (2), we get
– 226x – 226y = – 678
x + y = 3 …………….(3)
[Dividing throughout by -226]
Subtracting equation (2) from equation (1), we get
530x – 530y = 530
x – y = 1
[Dividing throughout by 530]
Adding equation (3) and equation (4), we get
2x = 4
x = \(\frac { 4 }{ 2 } \) = 2
Subtracting equation (4) from equation (3), we get
2y = 2
y = \(\frac { 2 }{ 2 } \) = 1
Hence, the solution of the given pair of linear equations is x = 2, y = 1.
Verification: Substituting z = 2, y = 1, we
find that both the equations (1) and (2) are satisfied as shown below:
152x – 378y = (152) (2) – (378)(1)
= 304 – 378 = – 74
– 378x + 152y
= ( – 378)(2) + (152)(1)
= – 736 + 152 = – 604
This verifies the solution.
![]()
Question 8
ABCD is a cyclic quadrilateral. Find the angles of the cyclic quadrilateral.
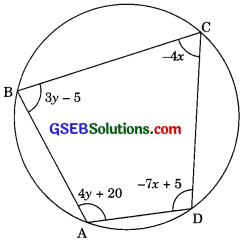
Solution:
We know that the opposite angles of a cyclic quadriLateral are supplementary, therefore,
\(\angle A \) + \(\angle C \) = 180°
4y + 20° + (-4x) = 180°
4y – 4x = 160°
y – x = 40° ………….. (1)
[Dividing theought by 4]
and, \(\angle B \) + \(\angle D \) = 180°
3y – 5° + (-7x + 5)° = 180°
3y – 5° – 7x + 5° = 180°
3y – 7x = 180° ……………. (2)
From equation (1),
y = 40° + x
Substituting this value of y In equation (2), we get
3(40° + x) – 7x = 180°
120°+ 3x – 7x = 180°
-4x = 60°
x = \(\frac { 60 }{ -4 } \) = – 15°
Subet.tutLng x = – 15° in equation (3), we get
y = 40° – 15° = 25°
\(\angle A \) 4(25) + 20 = 120°
\(\angle B \) = 3(25) – 5 = 70°
\(\angle C \) = – 4 x (-15) = 60°
\(\angle D \) = – 7 x (-15) + 5
= 105 + 5 = 110°
Hence, the anglee of the cyclic quadrilateral are
\(\angle A \) = 120°, \(\angle B \) = 70°, \(\angle C \) = 60°, and \(\angle D \) = 110°
Verification: Substituting x = – 15°, y = 25°,
we find that both the equations (I) and (2) are satisfied aa shown below.
y – x = 15 + 25 = 40°
3y – 7x = 7(15) + 3 (25)
= 105° + 75° = 180°
This verifies the solution.
![]()