Gujarat Board GSEB Solutions Class 10 Maths Chapter 4 Quadratic Equations Ex 4.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 4 Quadratic Equations Ex 4.1
Question 1.
Check whether the following are quadratic equations:
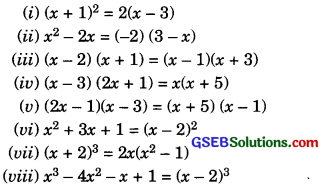
Solution:
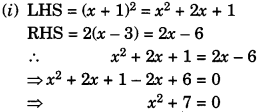
∴It is of the form ax2 + bx + c = 0, where
a = 1, b = 0, c = 7.
Hence, the given equation is a quadratic equation.
(ii) RHS = ( – 2)(3 – x) = – 6 + 2x
x2 – 2x = – 6 + 2x
x2 – 2x + 6 – 2x = 0
x2 – 4x + 6 = 0
It is ofthe form ax2 + bx + c = 0, where
a = 1, b = – 4, c = 6.
Hence, the given equation is a quadratic equation.
![]()
(iii) LHS = (x – 2)(x + 1)
– x2 – x – 2
RHS = (x – 1) (x + 3)
= x2 + 2x – 3
x2 – x – 2 = x2 + 2x – 3
– x – 2 – 2x + 3 = 0
-3x + 1 = 0
It is not of the form ax2 + bx + c = 0
Hence, the given equation is not a quadratic equation
(iv) LHS = (x – 3) (2x + 1)
= 2x2 – 6x + x – 3
= 2x2 – 5x – 3
RHS = x(x + 5) = x2 + 5x
2x2 – 5x – 3 = x2 + 5x
= 2x2 – x2 – 5x – 5x – 3 = 0
x2 – 10x – 3 = 0
It is of the form ax2 + bx + c = 0, where
a= 1, b=10, c = -3
Hence, the given equation is a quadratic equation

It is of the form ax2 + bx + c = 0
where a = 1, b = -11, c = 8
Hence, the given equation is a quadratic equation.
(vi) RHS = (x – 2)2 = x2 – 4x + 4
x2 + 3x + 1 =x2 – 4x +4
3x + 4x + 1 – 4 = 0
7x – 3 = 0
It is not of the form ax2 +bx + c = 0
Hence the given equation is not a quadratic equation.

It is not of the form ax2 +bx + c = 0
Hence the given equation is not a quadratic equation.
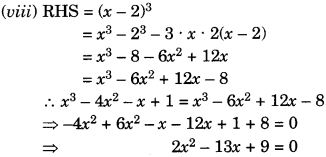
It is not of the form ax2 +bx + c = 0 where a = 2, b = -13, c = 9.
Hence the given equation is not a quadratic equation.
![]()
Question 2.
Represent the following problems situations in the form of quadratic equations:
(i) The area of a rectangle plot is 528 m2. The length of the plot (in metres) is one more than twice its breadth. Find the length and breadth of the plot.
(ii) The product of two consecutive positive integers is 306. Find the integers.
(iii) Rohan’s mother is 26 years older than him. The product of their ages 3 years from now will be 360. We would like to find Rohan’s present age.
(iv) A train travels a distance of 480 km at uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. Find the speed of the train.
Solution:
(i) Let breadth of the rectangle = x m. Then,
length of the rectangle = (2x + 1) m
∴ Area of the rectangle
= (2x + 1)xm2
According to the given condition,
(2x + 1)x = 528
2x2 + x – 528 = 0
which is a quadratic equation in x.
Solving this equation by factorization
method, we get
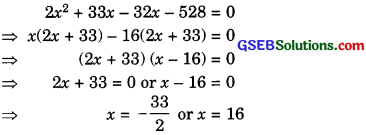
But breadth cannot be – ve.
∴ x = 16.
Hence, breadth of the rectangle = 16 m and
length of the rectangle = 2 x 16 + 1 = 33 m.
(ii) Let two consecutive positive integers are x and (x+ 1). Then
x (x + 1) = 306
x2 + x – 306 = 0
which is a quadratic equation in x.
Solving this equation by factorization
method, we get
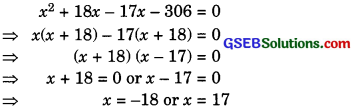
But integers are +ve.
∴ x = 17.
Hence, two consecutive positive integers are 17 and 18.
(iii) Let Rohan’s present age = x years
Then, Rohan’s mother age = (x + 26) years
Rohan’s age after 3 years (x + 3) years
and Rohan’s mother age after 3 years
= (x + 29) years
According to the given condition,
(x + 3) (x + 29) = 360
x2 + 32x + 87 = 360
x2 + 32x – 273 = 0
Which is a quadratic equation in r solving it by factorization method.
x2 + 39x – 7x – 273 = 0
x(x + 39) – 7(x + 39) = 0
(x + 39) (x – 7) = 0
= x + 39.
(or)
x = 7
But age cannot be -ve,
– x = 7
Hence, Rohan’s present age a 7 years.
(iv) Let the speed of the train = x km/h
Distance = 480 km
Time taken by the tram to cover the distance of 48Okm = \(\frac { 480 }{ x } \) h.
Now, according to the given condition,

which is a quadratic equation in x.
Solving it by factorization method,
x2 – 40x + 32x – 1280 = 0
= x (x – 40) + 32(x – 40) = 0
(x – 40) (x + 32) = 0
x – 40 = 0
(or)
x+32 = 0
x = 40
or
x = – 32.
But speed of the train cannot be – ve.
x = 40.
Hence, the speed of the train =40 km/h.
![]()