GSEB Solutions Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2

Gujarat Board GSEB Solutions Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2

Question 1.
Fill in the blanks in the following table. Given that a is the first term d the common difference and a the nth term of the AP.

Solution:
(i) a = 7, d = 3, n = 8, a = _n ?
than a_n = a + (n – 1) d
a_n = 7 + (8 – 1) 3
a_n = 7 + 7 x 3
a_n = 7 + 21
a_n = 28

(ii) a = – 18, d = ?, n = 10, a_n = 0
a_n = a + (n – 1) d
0 = – 18 + (10 – 1)d
= 18 = 9d
d = 2

(iii) a = ?, d = – 3, n = 18, a_n = – 5
a_n = a + (n – 1) d
– 5 = a + (18 – 1)(- 3)
– 5 = a + (- 51)
51 – 5 = a
a = 46

(iv) a = – 18.9, d = 2.5, n = ?, a_n = 3.6
a_n = a + (n – 1) d
3.6 = – 18.9 + (n – 1) x 2.5
3.6 + 18.9 = 2.5 (n – 1)
22.5 = 2.5 (n – 1)
n – 1 = \(\frac { 22.5 }{ 2.5 } \)
n – 1 = \(\frac { 225 }{ 25 } \)
n – 1 = 9
n = 9 + 1
n = 10

(v) a = 3.5, d = 0, n = 105, a_n = ?
a_n = a + (n – 1) d
a_n = 3.5 + (105 – 1) 0
a_n = 3.5

Question 2.
Choose the correct choice in the following and justify.
(i) 30th term of the AP: 10, 7, 4,….. is
(A) 97 (B) 77 (C) – 77 (D) – 87
(ii) 11th term of the AP: – 3, –\(\frac { 1 }{ 2 } \), 2, ….. is
(A) 28 (B) 22 (C) – 38 (D) 48 – \(\frac { 1 }{ 2 } \)
Solution:
(i) The given AP is 10, 7, 4, …
a = 10, d = 7 – 10 = – 3
n = 30
a_n = a + (n — 1) d
a₃₀ = 10 + (30 – 1) x (- 3)
= 10 + 29 x (- 3)
= 10 – 87
a₃₀ = – 77
hence the correct choice is (C).

(ii) In the given AP,
a = – 3
and
d = – \(\frac { 1 }{ 2 } \) – ( – 3) = \(\frac { -1 }{ 2 } \) + 3 = \(\frac { 5 }{ 2 } \)
a₁₁ = a + (n – 1)d
= – 3 + (11 – 1) x \(\frac { 5 }{ 2 } \)
= – 3 + 10 x \(\frac { 5 }{ 2 } \)
= – 3 + 25
a₁₁ = 22
Hence the correct choice is (B)

Question 3.
In the following APs, find the missing terms in the boxes.
(j) 2, 26
(ii) 13, 3
(iii) 5, 9\(\frac { 1 }{ 2 } \)
(iv) – 4, 6
(v) 38, – 22
Solution:
(i) Let the common difference of given AP is d
a = 2, a₃ = 26
a₃ = a + 2d = 26
a + 2d = 26
2 + 2d = 26
2d = 26 – 2
2d = 24
d = 12
Hence second term a₂ = a + d
a₂ = 2 + 12 = 14
Hence the’missing term in the box is .

(ii)
Let a be the first term and d be the common difference of given AP.
Then, a + d = 13
a₄ = a + 3d = 3

d = – 5
Putting value of d in equation (1)
a + d = 13
a + ( – 5) = 13
a = 13 + 5
a = 18
a₃ = a + 2d
= 18 + 2x ( – 5)
= 18 – 10
Hence the missing terms in the boxes are
and

(iii) Let common difference be d and a = 5
a₄ = a + 3d = 9\(\frac { 1 }{ 2 } \)
a + 3d = \(\frac { 19 }{ 2 } \)
5 + 3d = \(\frac { 19 }{ 2 } \)
= 3d = \(\frac { 19 }{ 2 } \) – 5
3d = \(\frac { 19 }{ 2 } \)
d = \(\frac { 9 }{ 2×3 } \) = \(\frac { 3 }{ 2 } \)
Now, a₂ = a + d = 5 + \(\frac { 3 }{ 2 } \)
= \(\frac { 10+3 }{ 2 } \) = \(\frac { 13 }{ 2 } \) = 6\(\frac { 1 }{ 2 } \)
a₃ = a + 2d = 5 + 2 x \(\frac { 3 }{ 2 } \)
a₃ = 8
Hence the missing terms are and in the boxes.

(iv) a = – 4 and we let d be the common difference.
Then a₆ = a + (n – 1) d
a₆ = – 4 + (6 – 1) x d
6 = – 4 + 5d
10 = 5d
d = 2
a₂ = a + d = – 4 + 2 = – 2
a₃ = a + 2d = – 4 + 2 x 2
= 4 + 4 = 0
a₄ = a + 3d = – 4 + 3 x 2
= – 4 + 6 = 2
a₅ = a + 4d = – 4 + 4 x 2
= – 4 + 8 = 4
Hence the missing terms in the boxes are

(v) Let common difference be d.
a₂ = a + d = 38
= a + d = 38 ……………(1)
a₆ = a + 5d = – 22 ……………. (2)

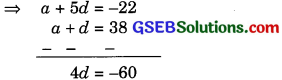
d = – 15
Putting value of d in equation (1)
a + d = 38
= a – 15 = 38
a = 38 + 15
a = 53
a₃ = a + 2d
a₃ = 53 + 2 ( – 15)
a₃ = 53 – 30
a₃ = 23
a₄ = a + 3d
a₄ = 53 + 3 x ( – 15)
a₄ = 53 – 45 = 8
a₅ = a + 4d
a₅ = 53 + 4 x ( – 15)
a₅ = 53 – 60
a₅ = – 7
Hence the missing terms in the boxes are
and

Question 4.
Which term of the AP 3, 8, 13, 18, ……. is 78 ?
Solution:
The given AP is 3, 8, 13, 18, ……………
a = 3
d = 8 – 3 = 5
Let the term of given AP is 78.
Hence a_n = a + (n – 1) d
78 = 3 + (n – 1) x 5
75 = (n – 1) x 5
n – 1 = \(\frac { 75 }{ 5 } \)
n – 1 = 15
n = 16
Hence 16th term of the given AP is 78.

Question 5.
Find the number of terms in each of the following APs.
(i) 7 13, 19, …, 205
(ii) 18, 15\(\frac { 1 }{ 2 } \),13,…,- 47
Solution:
(i) Given AP is 7, 13, 19, ………….., 205
a = 7, d = 13 – 7 = 6
Let n be the number of terms
then a_n = 205
a_n = a + (n – 1) d
205 = 7 + (n – 1) 6
= 205 – 7 = (n – 1) x 6
198 = (n – 1) x 6
\(\frac { 198 }{ 6 } \) = n – 1
= n – 1 = 33
n = 34
Hence the number of terms in the given AP is 34.

(ii) Given AP is 18, 15\(\frac { 1 }{ 2 } \), 13, …,- 47
a = 18, d = \(\frac { 31 }{ 2 } \) – 18 = \(\frac { -5 }{ 2 } \)
Let a_n = – 47
then a_n = a + (n – 1) d
– 47 = 18 + (n – 1) \(\frac { -5 }{ 2 } \)
– 47 = 18 – \(\frac { -5 }{ 2 } \) (n – 1)
7 – 18 = \(\frac { -5 }{ 2 } \)(n – 1)
– 65 = \(\frac { -5 }{ 2 } \)(n – 1)
\(\frac { 65×2 }{ 5 } \) = n – 1
26 = n – 1
= n – 1 = 26
= n = 26 + 1
n = 27
Hence the number of terms in the given AP is 27.

Question 6.
Check whether – 150 is a term of the AP: 11, 8, 5, 2, ………….
Solution:
The given list of numbers is 11, 8, 5, 2, ……..
a₂ – a₁ = 8 – 11 = – 3
Here a = 11, d = – 3
Let – 150 be the a_n term of the given AP.
then
a_n = a + (n – 1)d
– 150 = 11 + (n – 1)( – 3)
– 150 = 11 – 3n + 3
3n = 150 + 14
n = \(\frac { 164 }{ 3 } \)
But n must be positive integer therefore – 150 is not a term of given AP.

Question 7.
Find the 31st term of AP whose 11th term is 38 and 16th term is 73.
Solution:
Let a be the first term and cl is the common difference of the AP.
11th term, a₁₁ = 38 [a₁₁ = a + (11 – 1)d]
a + 10 d = 38 ……………….. (1)
And 16th term = 73

d = \(\frac { 35 }{ 5 } \) = 7
d = 7
Putting value of d an equation (1)
a + 10 d = 38
a + 10 x 7 = 38
a + 70 = 38
a = 38 – 70
a = – 32
there fore a_n = a + (n – 1)d
a₃₁ = – 32 + (31 – 1) x 7
a₃₁ = – 32 + 210
a₃₁ = 178
Hence 31 term of the AP is 178,

Question 8.
An AP cvneists of 50 terms ofwhich third tarms is 12 and last term is 106. Find the 29th terms.
Solution:
Let a be the first term and d be the common difference of AP.
Third terni a₃ = 12
a + 2d = 12
last term = 106 (l = 50th)
l = a + (n – 1)d
106 = a + (50 – 1) d
106 = a + 49d
a + 49d = 106 ………. (2)
Solving equations (1) and (2), we get
47d = 94
d = \(\frac { 94 }{ 47 } \)
Putting value of din equation (1)
a + 2d = 12
a + 2 x 2 = 12
a = 12 – 4
a = 8
Therefore 29th term
a₂₉ = a + 28d
= 8 + 28 x 2
= 8 + 56 = 64

Question 9.
If the 3rd and the Wit terms of an AP are 4 and -8 respectively, which term of this AP is zero?
solution:
Let a and d be the first term and common difference of an AP.
Third term a₃ = 4
a + 2d = 4
(a_n = a + (n – 1)d)
Ninth term a₉ = – 8
a + 8d = – 8 …………… (2)
Solving equations (1) and (2),

d = – 2
Putting value old in equation (2),
a + 8d = – 8
a + 8 x (- 2) = – 8
a – 16 = – 8
a = 8
Let the the nth term of the AP be zero
then a + (n – 1)d = 0
(a_n = a + (n – 1)d)
8 + (n – 1)( – 2) = 0
8 – 2n + 2 = 0
2n = 10
n = 5
Hence 5’ term of the AP is zero.

Question 10.
The 17th term of an AP exceeds 10th term by 7. Find the common difference.
Solution:
Let a be the first term and d be the common difference of the AP.
17th term = a + 16d
(a + (17 – 1) d)
and 10th term = a + 9d
According to problem
a₁₇ = a₁₀ + 7
a + 16d = a + 9d +7
7d = 7
d = 1
Hence common difference is 1.

Question 11.
Which term of the AP: 3, 15, 27, 39, ….. will be 132 more than its 84th term?
Solution:
Given AP is 3, 15, 27, 39, ……….
Here a = 3 and d = 15 – 3 = 12
4th term = a + 53d (a + (54 – 1)d)
According to problem
nth term = 54th term + 132
a + (n – 1)d = a + 53d + 132
3 + (n – 1) x 12 = 3 + 53 x 12 + 132
(n – 1) x 12 = 636 + 132
n – 1 = \(\frac { 768 }{ 12 } \)
= n – 1 = 64
n = 65
Hence 65th term will be 132 more than 54th term.

Question 12.
Two APs have the same common difference The difference between their 100th term is 100. What is the difference between 1000th terms?
Solution:
Let a and a be the Gral term of two APs respectively and ci be the saine cximrnon difference of the two APs.
Then 100th term of first AP = a₁ + 99d
(a₁₀₀ = a₁ + (100 – 1) d)
100th term of second AP = a₂ + 99d
According to problem
a₁ + 99d (a₂ + 99d) = 100
a₁ – a₂ = 100
Now we have
1000th term of lint AP = a₁ + 999d
and 1000th term of second AP
= a + 999d
Hence the difference of 1000th terms of both AP’s
a₁ + 999d – (a₂ + 999d)
= a₁ – a₂
= 100
Hence the difference of 1000th term of both the APs is also 100.

Question 13.
How many three.digit numbers are divisible by 7 ?
Solution:
Three digit numbers which are divisible by 7
are: 105, 112, 119, 126, …………, 994
a₂ – a₁ = 112 – 105 = 7
a₃ – a₂ = 119 – 112 = 7
a₄ – a₃ = 126 – 119 = 7
Since difference, between two consecutive terms is 7. So the three-digit numbers which an divisible by 7 are in AP.
a = 105
last term = 994
nth term = l
l = a + (n – 1) d
994 = 105 + (n – 1) x 7
994 – 105 = (n – 1) x 7
(n – 1) x 7 = 889
n – 1 = \(\frac { 889 }{ 7 } \)
n – 1 = 127
n = 128
Hence, 128 three digit numbers are divisible by 7.

Question 14.
How many multiples of 4 Lie between 10 and 250?
Solution:
Multiples at 4 which lies between 10 and 250
are 12, 16, 20, 24, ……….., 248
a₂ – a₁ = 16 – 12 = 4
a₃ – a₂ = 20 – 16 = 4
Since difference between two consecutive terms is 4 i.e. same so these numbers form an AP.
Here a = 12, and l = 248
l = a + (n – 1) d
12 + (n – 1) x 4 = 248
(n – 1) x 4 = 248 – 12
n – 1 = 59
n = 60
Hence 60 multiples of 4 between 10 and 250.

Question 15.
For what value of is, are the e terms of two
APs 63, 65, 67, ….. and 3, 10, 17, ……….. equal?
Solution:
First AP is 63. 65,67, ………
Here a = 63, and d = 65 – 63 = 2
nth term a + (n – 1)d
(a_n = a + (n – 1) d)
= 63 (n – 1) x 2
Second AP is 3,10, 17, ……….
a = 3 and d = 10 – 3 = 7
nth term = a + (n – 1) d
= 3 + (n – 1) = 7
According to problem nth terms are same.
63 + (n – 1) x 2 = 3 + (n – 1) x 7
63 + 2n – 2 = 3 + 7n – 7
61 + 2o = 7n – 4
– 5n = – 65
n = 13
Hence 13th term of both APa are equal.

Question 16.
Determine the AP whose third term 16 and the 7th term exceeds the 5th, term by 12.
Solution:
Let a and d be the first and the common difference of the AP respectively.
Third term a₃ = 16
n₃ = a + 2d
a + 2d = 16
and 7th term = a + 6d
5th term = a + 21d
According the problem
a₇ = a₅ + 12
a + 6d = a + 4d + 12
2d = 12
d = 6
Putting value old in eqn.(1)
a + 2d = 16
a + 2 x 6 = 16
a = 4
Hence required AP is.
a, a + d, a + 2d, a + 3d, ……….
4, 4 + 6, 4 + 2 x 6, 4 + 3 x 6, ……….
4, 10, 16, 22, …………

Question 17.
Find the 20 term from the la.t term of the AP: 3, 8, 13, …………. 253.
Solution:
Given AP is
3, 8, 13, ……….., 253
Here a = 3 and d = 8 – 3 = 5
20th term from the last = l – (n – 1)d
= 253 – (120 – 1) x 5
= 253 – 19 x 5
= 253 – 95 = 158
Hence the 20th term from the last term of the given AP is 158.
Alternate method
Given AP is 3, 8, 13, …………. 253
Here a =3 and d = 8 – 3 = 5
l = a + (n – 1)d
253 = 3 + (n – 1) x 5
250 = (n – 1) x 5
n – 1 = \(\frac { 250 }{ 5 } \)
n – 1 = 50
n = 51
term from the last = (51 – 20 + 1) term from the beginning.
= 32 term from the beginning
a_n term = a + (n – 1)d
a₃₂ = 3 + (32 – 1) x 5
= 3 + 31 x 5
= 3 + 155 = 158
Hence 20th term from the last term of the given AP is 158.

Question 18.
The sum of the 4th and 8th term of an AP is 24 and the sum of the 6th and 10th term is 44. Find the first three term of the AP.
Solution:
Let a be the first term and d be the common difference
4th term = a + 3d [a₄ = a + (4 – 1)d]
8th term = a + 7d [a₈ = a + (8 – 1)d]
According to the problem.
a₄ + a₈ = 24
a + 3d + a + 7d = 24
2a + 10 d = 24
a + 5d = 12
6th term = a + 5d [a₆ = a + (6 – 1)d]
10th term = a + 9d [a₁₀ = a + (10 – 1)d)
According to problem,
a₆ + a₁₀ = 44
a + 5d + a + 9d = 44
2a + 14d = 44

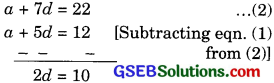
d = 5
Putting value, old in equ. (1)
a + 5d = 12
a + 5 x 5 = 12
a = 12 – 25
a = – 13
Therefore, first three terms of AP art
a, a + d and a + 2d
i.e.,-13, – 13 + 5 and -13 + 2 x 5
or, – 13, – 8 and -3

Question 19.
Subba Rao started work in 1995 at an annual salary of ₹ 5000 and received an increment of ₹ 200 each year. In which year did his income reach ₹ 7000?
Solution:
Here a = ₹ 5000
d = ₹ 200
l = ₹ 7000
Suppose in n years his income reached ₹ 7000,
Then
l – a + (n – 1)d
7000 = 5000 + (n – 1) 200
(n – 1) x 200 = 7000 – 5000
(n – 1) x 200 = 2000
n – 1 = \(\frac { 2000 }{ 200 } \)
n – 1 = 10
n = 11
In 11th year his salary becomes ₹ 7000.

Question 20.
Ramkali saved ₹ 5 In the Brat week of a year and then increased her weekly savings by ₹ 1.75. If in the nth week her weekly savings becomes ₹ 20,75, find n.
Solution:
Herr
a = ₹ 5
d = ₹ 1.75
a_n = 20.75
term of an AP.
a_n = a + (n – 1)d
20.75 = 5 + (n – 1)1.75
(n – 1)(1.75) = 15.75
n – 1 = \(\frac { 15.75 }{ 1.75 } \)
n – 1 = \(\frac { 1575 }{ 175 } \)
n – 1 = 9
n = 10
Hence required value of n is 10.