Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.3
Question 1.
Solve the following equations and check your results.
(i) 3x = 2x + 18
(ii) 5t – 3 = 3t – 5
(iii) 5x + 9 = 5 + 3x
(iv) 4z + 3 = 6 + 2z
(v) 2x – 1 = 14 – x
(vi) 8x + 4 = 3(x – 1) + 7
(vii) x \(\frac { 4 }{ 5 }\) (x +10)
(viii) \(\frac { 2x }{ 3 }\) + 1 = \(\frac { 7x }{ 15 }\) + 3
(ix) 2y + \(\frac { 5 }{ 3 }\) = \(\frac { 26 }{ 3 }\) – y
(x) 3m = 5m – \(\frac { 8 }{ 5 }\)
Solution:
(i) 3x = 2x + 18
Transposing 2x from RHS to LHS, we have
3x – 2x = 18 or x = 18
Check: Put x = 18 in LHS and RHS of the equation
LHS=3x
= 3 x 18 = 54
RHS = 2x + 18
= 2 x 18 + 18
= 36 + 18 = 54
Thus, LHS = RHS
![]()
(ii) 5t – 3 = 3t – 5
Transposing (-3) to RHS, we have
5t = 3t – 5 + 3 or 5t = 3t – 2
Transposing 31 to LHS, we have
5t – 3t = -2 or 21 = – 2
Diving both sides by 2, we have \(\frac { 2t }{ 2 }\) = \(\frac { -2 }{ 2 }\) or t = -1
Check: Put t = -1 in LHS and RHS of the equation
LHS = 5(-1) -3 = -5 -3 = -8
RHS = 3(-1) -5 = -3 -5 = -8
Thus, LHS = RHS
(iii) 5x + 9 = 5 + 3x
Transposing 9 to RHS, we have
5x = 5 + 3x -9 or 5x = -4 + 3x
Transposing 3x to LHS, we have
5x – 3x = -4 or 2x = -4
Dividing both sides by 2, we have
x = \(\frac { -4 }{ 2 }\) = \(\frac { 1 }{ 2 }\) – 2 or x = -2
Check: Put x = -2 in LHS and RHS of the equation
LHS = 5 x (-2) + 9 = -10 + 9 = -1
LHS = 5 + 3(-2) = 5-6 = -1
Thus, LHS = RHS
![]()
(iv) 4z + 3 = 6 + 2z
Transposing 3 to RHS, we have
4z = 6 – 3+ 2z or 4z = 3 + 2z
Transposing 2z to LHS, we have
4z – 2z = 3 or 2z = 3
Dividing both sides by 2, we have z = \(\frac { 3 }{ 2 }\)
Check: Put z = \(\frac { 3 }{ 2 }\) in LHS and RHS of the equation
LHS= 4×\(\frac { 3 }{ 2 }\)+3=6+3=9
RHS=6+2×\(\frac { 1 }{ 2 }\)=6+3=9 2
Thus, LHS = RHS
(v) 2x – 1 = 14 – x
Transposing (-1) to RHS, we have
2x = 14-x + 1 or 2x = 15 – x
Transposing (-x) to LHS, we have
2x + x = 15 or 3x = 15
Dividing both sides by 3, we have
x = \(\frac { 15 }{ 3 }\) = 5
∴ x = 5
Check: Put x = 5 in LHS and RHS of the equation
LHS = 2 × 5 – 1 = 10 – 1 = 9
RHS = 14 – 5 = 9
Thus, LHS = RHS
![]()
(vi) 8x + 4 = 3(x – 1) + 7
or 8x + 4 = 3x-3 + 7
or 8r + 4 = 3x + 4
Transposing 4 to RHS, we have
8x = 3x + 4 – 4
Transposing 3x to LHS, we have
8x – 3x = 0 or 5x =0
∴ x = 0
Check: Put x = 0 in LHS and RHS of the equation
LHS = 8X0 + 4 = 0 + 4 = 4
RHS = 3(0 – 1) + 7 = -3 + 7 = 4
Thus, LHS = RHS
(vii) x \(\frac { 4 }{ 5 }\) (x +10)
Transposing \(\frac { 4 }{ 5 }\) x to LHS, we have
x – \(\frac { 4 }{ 5 }\) x = 8 or \(\frac { 5x – 4x }{ 5 }\) = 8 or \(\frac { x }{ 5 }\) = 8
Multiplying both sides by 5, we have
x = 8 x 5 = 40
∴ x = 40
Check: Put x = 40 in LHS and RHS of the equation
LHS = 40
RHS = \(\frac { 4 }{ 5 }\)(40+10) = \(\frac { 4 }{ 5 }\) × 50 = 4 × 10 = 40
Thus, LHS = RHS
![]()
(viii) \(\frac { 2x }{ 3 }\) + 1 = \(\frac { 7x }{ 15 }\) + 3
Transposing 1 to RHS, we have
\(\frac { 2x }{ 3 }\) – \(\frac { 7x }{ 15 }\) + 3 – 1 or \(\frac { 2x }{ 3 }\) = \(\frac { 7x }{ 15 }\) + 2
Transposing \(\frac { 7x }{ 15 }\) to LHS, we have
\(\frac { 2x }{ 3 }\) – \(\frac { 7x }{ 15 }\) = 2 or \(\frac { 10x – 7x }{ 15 }\) = 2 or or \(\frac { 3x }{ 15 }\) = 2
Multiplying both sides by 15, we have 3x = 2 x 15 = 30
Dividing both sides by 3, we have
\(\frac { 3x }{ 3 }\) = \(\frac { 30 }{ 3 }\)
∴x = 10
Check: Put x = 10 in LHS and RHS of the equation
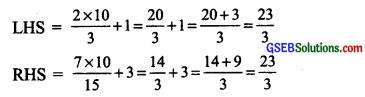
Thus, LHS = RHS
(ix) 2y + \(\frac { 5 }{ 3 }\) = \(\frac { 26 }{ 3 }\) – y

(x) 3m = 5m – \(\frac { 8 }{ 5 }\)
Transposing 5m to LHS, we have
3m – 5m = –\(\frac { 8 }{ 5 }\) or -2m = –\(\frac { 8 }{ 5 }\)
Dividing both sides by (-2), we have

Thus, LHS = RHS