Gujarat Board GSEB Solutions Class 10 Maths Chapter 6 Triangle Ex 6.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 6 Triangle Ex 6.2
Question 1.
In figure (i) and (ii). DE II BC. Find EC in (i) and AD in (ii).
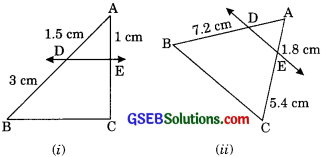
Solution:
(i) In ∆ABC
\(\frac {AD}{DB}\) = \(\frac {AE}{EC}\)
⇒ \(\frac {1.5}{3}\) = \(\frac {1}{EC}\)
EC = \(\frac {3}{1.5}\)
EC = \(\frac {3}{1.5}\) = 2 cm
Question 2.
E and F are points on the sides PQ and PR respectively of a PQR. For each of the following cases. State whether EF || QR.
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm, and FR = 2.4 cm.
(ii) PE =4 cm, QE = 4.5 cm, PF = 8 cm, and RF = 9 cm.
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm, and PF = 0.36 cm.
Solution:
(i) We have
PE = 3.9 cm, EQ = 3 cm PF = 3.6 cm and FR = 2.4 cm
then \(\frac {PE}{EQ}\) = \(\frac {3.9 cm}{3}\) = \(\frac {1.3}{1}\) ………(1)
and \(\frac {PF}{FR}\) = \(\frac {3.6}{2.4}\) = \(\frac {3}{2}\) \(\frac {1.5}{1}\) ……. (2)
From equation (1) and (2) we have
\(\frac {PE}{EQ}\) – \(\frac {PF}{FR}\) (by converse of BPT)
Therefore EF is not parallel to QR.
![]()
(ii) We have
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
then,
\(\frac {PE}{EQ}\) = \(\frac {4}{4.5}\) = \(\frac {40}{45}\) = \(\frac {8}{9}\) ……….(1)
and = \(\frac {PE}{RF}\) = \(\frac {8}{9}\) ……….(2)
from equation (1) and (2)
We get = (by converse of BPT)
therefore EF || QR
(iii) We have
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
\(\frac {PE}{EQ}\) = \(\frac {18}{110}\)
\(\frac {PE}{EQ}\) = \(\frac {9}{55}\) ………(1)
and \(\frac {PE}{FR}\) = \(\frac{0.36}{2.56-0.36}\)
⇒ \(\frac {PE}{FR}\) = \(\frac{0.36}{2.20}=\frac{36}{220}\)
⇒ \(\frac {PE}{FR}\) = \(\frac{9}{55}\) ………(2)
\(\frac {PE}{EQ}\) = \(\frac {PE}{FR}\)
Therefore EF || QR (by converse of BPT)
Question 3.
In figure, if LM || CB and LN || CD, prove that (AI 2010)
\(\frac {AM}{AB}\) = \(\frac {AN}{AD}\)
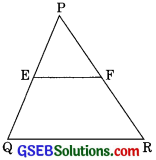
Solution:
LM || BC
\(\frac {AM}{MB}\) = \(\frac {AL}{LC}\) (by BPT) ……. (1)
Now, in ∆ACD
LN || CD
Therefore = (by BPT) ……..(2)
From equation (1) and (2)
\(\frac {AM}{MB}\) = \(\frac {AN}{ND}\)
or \(\frac {MB}{AM}\) = \(\frac {ND}{AN}\) (by Invertendo)
\(\frac {MB}{AM}\) + 1 = \(\frac {ND}{AN}\) + 1 (adding 1 both sides)
\(\frac{MB + AM}{AM}\) = \(\frac{ND + AN}+{AN}\)
⇒ \(\frac{AB}{AM}\) = \(\frac{AD}{AN}\)
⇒ \(\frac{AM}{AB}\) = \(\frac{AN}{AD}\) (by Invertendo)
![]()
Question 4.
In figure, DE || AC, and DF || AE prove that
\(\frac{BF}{FE}\) = \(\frac{BE}{EC}\)
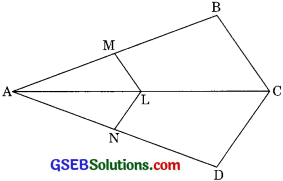
Solution:
In ∆ABE
DF || AE
\(\frac{AD}{BD}\) = \(\frac{FE}{BF}\) ………(1) (by BPT)
In ∆ABC
DE || AC
\(\frac{AD}{DB}\) = \(\frac{EC}{BE}\) ……..(2) (ByBPT)
From equation (1) and (2)
\(\frac{FE}{BF}\) = \(\frac{EC}{BE}\)
\(\frac{BF}{FE}\) = \(\frac{BE}{EC}\) (by Invertendo)
![]()
Question 5.
In figure DE || OQ and DF || OR. Show that EF || QR. (Foreign 2008)
Solution:
In ∆POQ
DE || OQ
\(\frac{PE}{EQ}\) = \(\frac{PD}{DO}\) ………(1) (ByBPT)
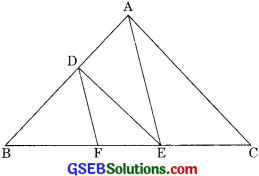
Now, in ∆PRO
DF || OR
Therefore = \(\frac{PD}{DO}\) = \(\frac{PF}{FR}\) ……..(2) (by BPT)
From eqn (1) and (2) we get
\(\frac{PE}{EQ}\) = \(\frac{PF}{FR}\)
Therefore EF || QR (by converse of BVT)
Question 6.
In figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR. (CBSE 2007)
Solution:
In ∆OPQ
AB || PQ
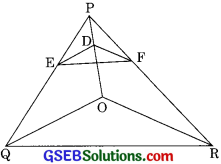
then = \(\frac{OA}{AP}\) = \(\frac{OB}{BQ}\) ……(1) (by BPT)
In ∆OPR
AC || PR (given)
then = \(\frac{OA}{AP}\) = \(\frac{OC}{CR}\) ……. (2) (by BPT)
From equation (1) and (2)
\(\frac{OB}{BQ}\) = \(\frac{OC}{CR}\)
Therefore BC || QR (by converse of BPT)
![]()
Question 7.
Using theorem 6.1 (i.e. Basic proportionality theorem), prove that line drawn through the mid point of one side of a triangle parallel to another side bisects the third side (Recall that you have proved it in class IX) (CBSE 2012)
Solution:
Given:
∆ABC in which, D is the midpoint of AB and
DE || BC
To prove: E is the midpoint of AC
Proof: In ∆ABC
DE || BC (given)
then \(\frac{AD}{DB}\) = \(\frac{AE}{EC}\) ………(1) (by BPT)
∵ D is the midpoint of AB then
AD = DB
Putting this value in eqn (1) we get
\(\frac{DB}{DB}\) = \(\frac{AE}{EC}\)
⇒ 1 = \(\frac{AE}{EC}\)
⇒ AE = EC
Hence E is the midpoint of AC.
![]()
Question 8.
Using theorem 6.2 (i.e. Converse of basic proportionality theorem), prove that the line joining the midpoints of any two sides a triangle is a parallel to the third side (Recall that you have done it in class IX)
Solution:
Given: ∆EC in which D and E are the midpoints of sides AB and AC respectively. DE is the line joining D and E.
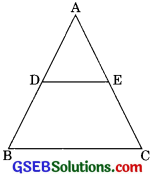
To prove: DE || BC
Proof: D is the mid point of AB
Then AD = DB
∴ \(\frac{AD}{DB}\) = 1 …….(1)
Similarly
\(\frac{AE}{EC}\) = 1 (AE = EC)
From equation (1) and (2)
\(\frac{AD}{DB}\) = \(\frac{AE}{EC}\)
Therefore DE || BC (by converse of BPT)
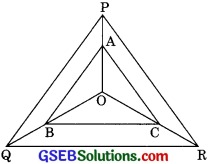
Question 9.
ABCD is a trapezium in which AB || DC and its diagonal intersect each other at the point O. Show that = \(\frac{AO}+{BO}\) = \(\frac{CO}{DO}\) (CBSE 2004)
Solution:
Given: ABCD is a trapezium in which AB || DC and diagonals of trapezium intersect each other at O.
To prove: = \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\)
Construction: Through O, draw a line 0E parallel to AB which intersect AD at E.
Proof: In ∆ADC
OE || DC
AB || DC and OE || AB then OE ||DC
then = \(\frac{AO}{CO}\) = \(\frac{AE}{DE}\) ……..(1) (By BPT)

In ∆ DBA
OE || AB
\(\frac{DE}{AE}\) = \(\frac{DO}{BO}\) (By BPT)
⇒ \(\frac{AE}{DE}\) = \(\frac{BO}{DO}\) (by Invertendo) ……(2)
From equations (1) and (2)
\(\frac{AO}{CO}\) = \(\frac{BO}{DO}\)
⇒ \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\) (by Alternendo)
![]()
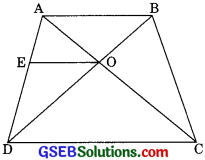
Question 10.
The diagonals of quadrilateral ABCD intersect each other at the point O such that \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\) , show that ABCD is a trapezium. (CBSE 2012)
Solution:
Given: ABCD is a quadrilateral whose diagonals intersect each other at O such that
\(\frac{AO}+{BO}\) = \(\frac{CO}+{DO}\)
To Prove: ABCD is a trapezium.
Construction: Draw a line 0E AB which intersect AD at E.
Proof: In ∆DAB
DO || DE (by construction)
then = \(\frac{DO}{BO}\) = \(\frac{DE}{AE}\) ……….(1)
But = \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\) (Given)
⇒\(\frac{DO}{BO}\) = \(\frac{CO}{AO}\) ……..(2)
from equation (1) and (2)
\(\frac{CO}{AO}\) = \(\frac{DE}{AE}\)
or \(\frac{AO}{CO}\) = \(\frac{AE}{DE}\) (by Invertendo)
∴ In ∆ADC
OE || CD (by converse of BPT)
But OE || AB (by construction)
therefore AB ||CD
Hence quadrilateral ABCD is a trapezium.