Gujarat Board GSEB Solutions Class 10 Maths Chapter 6 Triangle Ex 6.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 10 Maths Chapter 6 Triangle Ex 6.3
Question 1.
State in which pairs of triangles in the figures are similar. Write the similarity criteria used by you for answering the question and also write the pairs of similar triangles in the symbolic form.
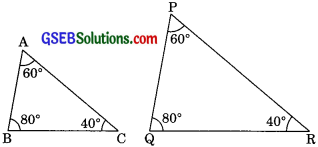
Solution:
(i) In ∆ABC and ∆PQR
∠A = ∠P (each 60°)
∠B = ∠Q (each 80°)
∠C = ∠R (each 40°)
Corresponding angles of ABC are equal
∴ ∆ABC ~ ∆PQR (by AAA Similarity)
(ii) In ∆ABC and ∆QRP

\(\frac{AB}{QR}\) = \(\frac{2}{4}\)= \(\frac{1}{2}\)
\(\frac{BC}{RP}\) =\(\frac{2.5}{5}\)= \(\frac{1}{2}\)
\(\frac{CA}{PQ}\)=\(\frac{3}{6}\) =\(\frac{1}{2}\)
\(\frac{A B}{Q R}=\frac{B C}{R P}=\frac{C A}{P Q}\)
![]()
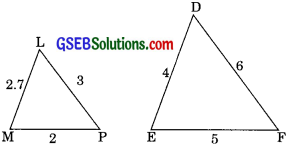
(iii) in ∆LMP and ∆DEF
\(\frac{LM}{DE}=\frac{2.7}{4}\)
\(\frac{M P}{E F}=\frac{2}{5}\)
\(\frac{\mathrm{AB}}{\mathrm{QR}}=\frac{2}{4}=\frac{1}{2}\)
\(\frac{LP}{DF}=\frac{3}{6}\)
⇒ \(\frac{\mathrm{LM}}{\mathrm{DE}} \neq \frac{\mathrm{MP}}{\mathrm{EF}} \neq \frac{\mathrm{LP}}{\mathrm{DF}}\)
therefore ∆LMP and ∆DEF are not similar.
(iv) In ∆MNL and PQR
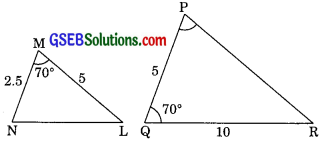
\(\frac{\mathrm{ML}}{\mathrm{QR}}=\frac{5}{10}=\frac{1}{2}\)
\(\frac{\mathrm{MN}}{\mathrm{QP}}=\frac{2.5}{5}=\frac{1}{2}\)
∴ \(\frac{M L}{Q R}=\frac{M N}{Q P}\)
and ∠NML = ∠QPR (each 700)
∴ ∆MNL ~ ∆PQR (by SAS similarity)
(v) In ABC and ∆DEF
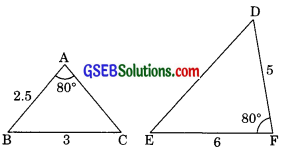
∠A = ∠F (each 800)
Included sides of ∠A in ∆DEFABC are not given while in ∆DEF included sides are given.
Therefore property of similarity will not be applied in this case.
(vi) In ∆DEF and ∆PQR
∠F = 180° – (70° + 80°)
= 180° – 150° = 30°
∠P = 180° – (80° + 30°)
∠p = 70°
∠D = ∠P (each 70°)
∠E = ∠Q (each 80°)
∠F = ∠R (each 30°)
Hence ∆DEF ~ ∆PQR (by AAA similarity)
![]()
Question 2.
In the figure ∆ODC – ∆OBA, ∆BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB
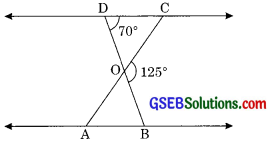
Solution:
We have
∠BOC = 125°
and ∠CDO = 70°
Since ∠DOC + ∠BOC = 1800 (linear pair)
∠DOC + 125° = 1800
∠DOC = 180° – 125°
∠DOC = 55° ……….(1)
In ∆DOC
∠DCO + ∠CDO + ∠DOC = 180°
(by angle sum property)
∠DCO + 70° + 55° = 180°
∠DCO 180° – 125°
∠DCO = 55° ……..(2)
Since ODC – ∠OBA (given)
∠OCD = ∠OAB = 55° ………(3)
(corresponding angle of similar triangles)
Hence, ∠DOC = 55°, ∠DCO = 55°
∠OAB = 55°
![]()
Question 3.
Diagonal AC and BD of a trapezium ABCD with AB DC intersect each other at the point O. Using a similarity criterion for two triangles, show that = \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OB}}{\mathrm{OD}}\)
Solution:
We have a trapezium ABCD in which AB || DC. And the diagonals AC and BD intersect at O.
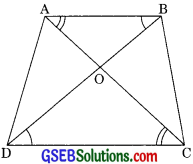
Now in ∆OAB and ∆OCD
AB || DC (given)
∠OBA = ∠ODC (alternate interior angles)
and ∠OAB = ∠OCD (alternate interior angles)
∴ ∆OAB ~ ∆OCD (by AA similarity)
Hence, = \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OB}}{\mathrm{OD}}\)
(corresponding sides of similar triangle)
Question 4.
In the given figure. \(\frac {QR}{QS}\) = \(\frac {QT}{PR}\) and ∠1 = ∠2, show that ∆PQS ~ ∆TQR
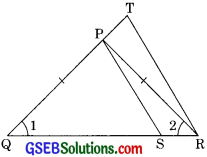
Solution:
In ∆PQR
∠1 = ∠2
PR = PQ
(In a triangle sides opposite to equal angles are equal)
\(\frac {QR}{QS}\) = \(\frac {QT}{PR}\) …….(2) (given)
from equation (1) and (2)
\(\frac {QR}{QS}\) = \(\frac {QT}{QP}\)
\(\frac {QR}{QS}\) = \(\frac {QP}{QT}\)
Now in ∆PQS and ∆TQR
\(\frac {QR}{QS}\) = \(\frac {QP}{QT}\) (proved above)
∠SQP = ∠RQT = ∠1 (common)
∴ ∆PQS ~ ∆TQR (by SAS similarity)
![]()
Question 5.
S and T are points on sides PR and QR of ∆PQR such that ∠P = ∠RTS. Show that ∆RPQ – ∆RTS. (CBSE 2012)
Solution:
We have T is a point on QR and S is a point on PR.
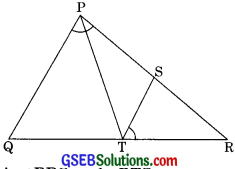
Now in ∆RPQ and ∆RTS
∠RPQ = ∠RTS (given)
and ∠PRQ = ∠TRS (common)
∴ ∆RPQ ~ ∆RTS (by AA similarity)
Question 6.
In figure, if ∆ABE MCD, show that ∆ADE – ∆ABC.
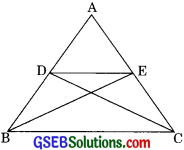
Solution:
We have
∆ABE = ∆ACD
Then AB = AC ……(1) (by CPCT)
AE = AD …….(2) (by CPCT)
Dividing equation (1) by equation (2)
\(\frac {AB}{AE}\) = \(\frac {AC}{AD}\)
\(\frac {AB}{AE}\) = \(\frac {AC}{AE}\) (AE = AC) ……..(1)
Now in ∆ADE and ∆ABC
\(\frac {AB}{AD}\) = \(\frac {AC}{AE}\) (from eqn (1) proved above)
∠DAE = ∠BAC (common)
∠ADE ~ ∠ABC (by SAS similarity)
![]()
Question 7.
In the figure, altitude AD and CE of ∆ABC intersect each other at the P. Show that
(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC
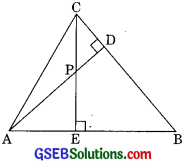
Solution:
∆ABC In which AD and CF intersect each other at P.
(i) In ∆AEP and ∆CDP
∠AEP = ∠CDP (each 90°)
∠APE = ∠CPD (vertically opposite angles)
∴ ∆AEP ~ ∆CDP (by AA Similarity)
(ii) In ∆ABD and ∆CBE
∠ADB = ∠CEB (each 90°)
∠ABD =∠CBE (common)
∆RD ~ ACRE (by AA similarity)
(iii) In ∆AEP and ∆ADB
∠AEP = ∠ADP (each 90°)
and ∠EAP = ∠DAB (common)
∴ ∆AEP ~ ∆ADB (by AA similarity)
![]()
(iv) In ∆PDC and ∆BEC
∠PDC = ∠BEC (each 90°)
and ∠DCP = ∠ECB (common)
∴ ∆PDC ~ ∆BEC (by AA similarity)
Question 8.
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ABE ~ ∆CFB.
Solution:
A parallelogram ABCD in which AD is produced to E and BE is pointed such that BE intersects CD at F.

Now, in ∆ABE and ∆CFB
∠BAE = ∠FCB
(opposite angle of || are equal)
∠AEB = ∠CBF ( AE || BC alternate interior angles)
∆ABE ~ ∆CFB (by AA similarity)
![]()
Question 9.
In the figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that
(i) ∆ABC ~ ∆AMP
(ii) \(\frac {CA}{PA} \) = \(\frac {BC}{MP} \)

Solution:
Given: MEC and AAMP are two right angle triangles right angled at B and M respectively.
To prove:
(i) ∆ABC – ∆AMP
(ii) \(\frac {CA}{PA} \) = \(\frac {BC}{MP} \)
Proof: (i) In ∆ABC and ∆AMP
∠ABC = ∠AMP (each 90°)
∠BAC = ∠MAP (common)
∆ABC ~ ∆AMP (AA similarity)
(ii) We have, ∆ABC – ∆AMP (proved above)
⇒ \(\frac {CA}{PA} \) = \(\frac {BC}{MP} \)
(corresponding sides of two similar triangles are proportional)
![]()
Question 10.
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ABC and EFG respectively. If ∆ABC ~ ∆FEG show that
(i) \(\frac {CD}{GH} \) = \(\frac {AC}{FG} \)
(ii) ∆DCB ~ ∆HGE
(iii) ∆DCA ~ ∆HGF
Solution:
We have two similar ∆ABC and ∆FEG such that CD and GH are the bisectors of ∠ACB and ∠FGE respectively.
(i) 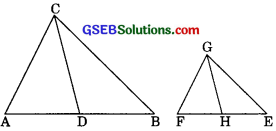
In ∆ACD and ΔFGH
∠CAD = ∠GFH
(corresponding angle of similar triangle ∆kBC ~ ∆FEG)
∠ACB = ∠FGE
(corresponding angle of similar triangle)
⇒ \(\frac{\angle \mathrm{ACB}}{2}=\frac{\angle \mathrm{FGE}}{2}\)
(Dividing by 2 on both sides)
∠ACD = ∠FGH
(CD is the bisector of ∠ACB and GH is the bisector of ∠FGE)
∴ ∆ACD ~ ∆FGH (by AA similarity)
⇒ \(\frac{C D}{G H}=\frac{A C}{F G}\)
(corresponding sides of two similar triangles are proportional)
![]()
(ii) In ∆DCB and ∆HGE
∠DBC = ∠HEG
(corresponding angles of similar triangle)
∠ACB = ∠FGE (Proved)
Dividing by 2 on both sides
⇒ \(\frac{\angle \mathrm{ACB}}{2}=\frac{\angle \mathrm{FGE}}{2}\)
⇒ ∠BCD = ∠HGE
∴ ∆DCB ~ ∆HGE (by AA similarity)
(iii) In ∆DAC and ∆HGF
∠DAC = ∠HFG
(corresponding angle of two similar triangle)
∠ACB = ∠EGF (Proved)
Dividing by 2 on both sides
⇒ \(\frac{\angle \mathrm{ACB}}{2}=\frac{\angle \mathrm{EGF}}{2}\)
∠ACD = ∠HGF
∴ ∆DCA ~ ∆HGF (by AA similarity)
![]()
Question 11.
In figure, E is a point on side CB produced on an isosceles triangle ABC with AB = AC. If AD⊥BC and EF⊥AC, Prove that ∆ABD ~ ∆ECF. (CBSE 2012)
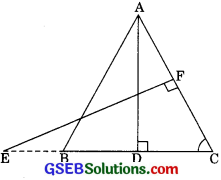
Solution:
Given: ∆ABC is an isosceles triangle, E is a point on BC produced
AB = AC
Also AD ⊥ BC andEF ⊥ AC
To Prove: ∆ABD – ∆ECF
Proofs In ∆ABD and ∆ECF
∠ABD = ∠ECF
(AB = AC, angle opposite to equal sides are equal)
and ∠ADB = ∠EFC (each 90°)
∠ABD – ∠ECF (by AA similarity)
Question 12.
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆PQR (see figure). Show that ∆ABC ~ ∆PQR.
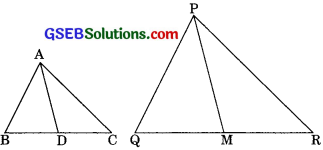
Solution:
We have ∆ABC and ∆PQR in which
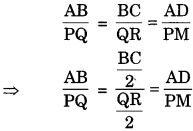
(\(\frac{BC}{2}\) = BD, \(\frac{QR}{2}\) = QM (because AD and PM are the medians of ∆ABC and ∆PQR)
⇒ \(\frac{A B}{P Q}=\frac{B D}{Q M}=\frac{A D}{P M}\)
∆ABD ~ ∆PQM (by SSS similarity)
Therefore their corresponding angles are equal)
∴ ∠ABD = ∠PQM
∠ABC = ∠PQR
Now in ∆ABC and ∆PQR
\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}\) ……….(1) (given)
and ∠ABC = ∠PQR ……..(2) (proved above)
From equation (1) and (2)
∆ABC ~ ∆PQR (by SAS)
![]()
Question 13.
D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB x CD. (CBSE 1994, 1995, 1998, 2004, 2012)
Solution:
in ∆ABC and ∆DAC
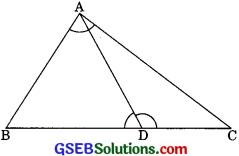
We have ∠ADC = ∠BAC (given)
and ∠DCA = ∠ACB (common)
∴ ∆DAC ~ ∆ABC (by AA similarity criterian)
\(\frac{CB}{CA}=\frac{CA}{CD}\) or CA2 = CB x CD
![]()
Question 14.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆PQR.
Solution:
In ∆ABC and ∆QPR in which
\(\frac{AB}{PQ}=\frac{AC}{PR}=\frac{AD}{PM}\) …….(1)
AD is the median of AABC therefore D is the mid point of BC. And PM is the median of APQR therefore M is the mid point of QR. Produce AD to E such that DE = AD and PM to
N such that MN = PM.
Then quadrilaterals AREC and PQNR are parallelograms.
(because diagonals of parallelogram bisect each other)
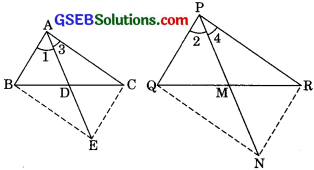
Hence BE = AC
and QN = PR (opposite sides of a II)
∴ \(\frac{BE}{QN}\) =\(\frac{AC}{PR}\) ………(2)
But \(\frac{AB}{PQ}=\frac{AC}{PR}=\frac{AD}{PM}\) (given)
![]()
Hence = \(\frac{AB}{PQ}=\frac{AC}{PR}=\frac{AD}{PM}\)
⇒ \(\frac{BE}{QN}=\frac{AB}{PQ}=\frac{AD}{PM}\)
\(\frac{BE}{QN}=\frac{AB}{PQ}=\frac{2AD}{2PM}\)
⇒ \(\frac{BE}{QN}=\frac{AB}{PQ}=\frac{AE}{PN}\)
and PN = 2PM by construction)
∆ABE – ∆PQN (by SSS similarity)
∠1 = ∠2 ………(3)
(corresponding angle of similar triangle)
Similarly ∆ACE – ∆PRN
Then ∠3 = ∠4 …..(4)
(corresponding angles of similar triangles) Adding eqn (3) and(4) we get
∠ 1 + ∠3 = ∠2 + ∠4
∠BAC =∠ QPR
also ∆ABC ~ ∆PQR (by SAS similarity)
![]()
Question 15.
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution:
Le ∆AB = 6m be the pole and BC = 4m be its shadow whereas the shadow of tower is 28 m
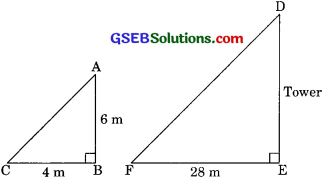
i.e. EF = 28 m
In ∆ABC and ∆DEF
∠ABC = ∠DEF (each 90°)
∠BAC = ∠EDF
(angle of deviation of sun at the same time)
∴ ∆ABC – ∆PQR (by AA similarly)
Corresponding sides of similar triangles are proportional.
Hence = \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}\)
⇒ \(\frac {6}{DE}\) = \(\frac {4}{28}\)
⇒ \(\frac {6}{h}\) = \(\frac {4}{28}\)
(Height of tower DE = h say)
6 x 28 = 4h
⇒ h = \(\frac{6 \times 28}{4}\)
h = 42 m.
![]()
Question 16.
If AD and PM are medians of triangles ∆ABC and ∆PQR, respectively where ∆ABC ~ ∆PQR.
Prove that: = \(\frac{A B}{P Q}=\frac{A D}{P M}\)
Solution:
Given: AD and PM are medians of triangle ABC and PQR, where ∆ABC ~ ∆PQR
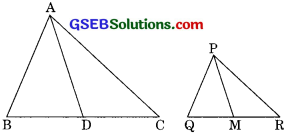
To Prove: \(\frac{A B}{P Q}=\frac{A D}{P M}\)
Proof: ∆ABC ~ ∆PQR (given)
\(\frac{A B}{P Q}=\frac{BC}{QR}=\frac{A C}{P R}\) …….(1)
Corresponding sides of two similar triangles are proportional.
∠ABC = ∠PQR
(corresponding angles of two similar triangles are equal)
⇒ ∠ABD = ∠PQM ………(2)
from eqn (1)
\(\frac{A B}{P Q}=\frac{BC}{QR}\)
\(\frac{A B}{P Q}=\frac{2B D}{2Q M}\)
\(\frac{A B}{P Q}=\frac{B D}{Q M}\) ………..(3)
In ∆ABD and ∆PQM
\(\frac{A B}{P Q}=\frac{BD}{QM}\)
and, ∠ABD = ∠PQM
∴ ∆ABD = ∆PQM(by SAS)
∴ \(\frac{A B}{P Q}=\frac{AD}{PM}\)
(corresponding sides of two similar triangles are proportional)