GSEB Solutions Class 10 Maths Chapter 6 Triangle Ex 6.5

Gujarat Board GSEB Solutions Class 10 Maths Chapter 6 Triangle Ex 6.5 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 10 Maths Chapter 6 Triangle Ex 6.5

Question 1.
Sides of triangles are given below. Determine which of these are right triangle. Write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Solution:
(i) 7 cm, 24 cm, 25 cm.
Here 72 = 49cm
24² = 576 cm
25² = 625 cm
we observed that
49 + 576 = 625
7² + 24² = 252
The given triangle is right angled triangle.
Hypotenuse = 25 cm

(ii) 3 cm, 8 cm, 6 cm
Here 32 = 9cm
82 = 64 cm
62 = 36 cm
we observed that
3² + 6² + 8²
The given triangle is not right angled triangle.

(iii) 50 cm, 80 cm, 100 cm.
Here 50² = 2500 cm
80² = 6400 cm
100² = 10,000 cm
We observed that
50² + 80² ≠ 100²
The given triangle is not right angled.

(iv) 13 cm, 12 cm, 5 cm.
Here 13² = 169 cm
12² = 144 cm
5² = 25 cm
we observed that
12² + 5² = 13²
∴ The given triangle is not right angled.
Hypotenuse = 13 cm

Question 2.
PQR is a triangle right angled at P and M is a point on QR such that PM⊥QR. Show that
PM² = QM.MR.
Solution:

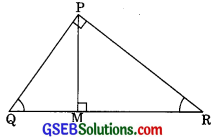
In ∆QMP and ∆QPR
∠QMP = ∠QPR (each 90°)
∠PQM = ∠PQR (Common)
∴ ∆PQM – ∆QPR ………(1) (by AA similarity)

Again in ∆PMR and ∆QPR
∠PMR = ∠QPR (each 900)
∠PRM = ∠QRP (Common)
∴ ∆PMR – ∆DQPR ………(2)
From (1) and (2)
∆QMP ~ ∆PMR
\(\frac{Q M}{P M}=\frac{P M}{R M}\)
(The corresponding sides of similar triangles are proportional)
PM² = QM.RM

Question 3.
In the figure ABD is a triangle, right angled at A and AC ⊥BD. Show that
(i) AB² = BC BD
(ii) AC² = BC DC
(iii) AD² = BD . CD (CBSE 2010)

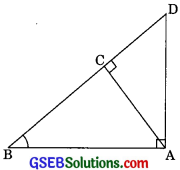
Solution:
(i) In ∆ABC and ∆BAD
∠ACB = ∠BAD (each 900)
∠ABC = ∠ABD (common)
∆BAC ~ ∆BDA (AA similarity)
\(\frac{A B}{D B}=\frac{B C}{B A}\)
(Corresponding sides are proportional)
⇒ AB² = BC.BD

(ii) In ∆ABC
∠BAC + ∠CBA = 90° ………(1) (by angle sum property)
In ∆ABD
∠BDA + ∠CBA = 90° …….(2)
From eqn (1) and (2)
∠BAC + ∠CBA = ∠BDA + ∠CBA
∠BAC = ∠BDA
In ∆ACB and ∆DCA
∠ACB = ∠DCA (each 900)
∠BAC = ∠BDA
(proved above from eqn (3))
∴ ∆ACB ~ ∆DCA (by AA similarity)
\(\frac{AC}{DC}=\frac{BC}{AC}\)
(corresponding sides of two similar triangle are proportional)
⇒ AC² = BC.DC

(iii) In ∆ADB and ∆CDA
∠DAB = ∠DCA (each 900)
∠ADB = ∠CDA (Common)
∴ ∆ADB ~ ∆CDA (by AA similarity)
Hence = \(\frac{AD}{CD}=\frac{BD}{CD}\)
(Corresponding sides of two similar triangles are proportional)
⇒ AD² = BD.CD

Question 4.
ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC². (CBSE 2012)
Solution:
We have ∆ABC is right angled such that
∠C = 90° and AC = AB

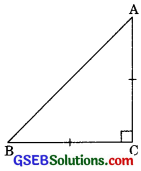
Applying Pythagoras theorem
– AC² + BC²
= AC² + AC² (BC = AC given)
Thus AB² = 2AC²

Question 5.
ABC is an isosceles triangle with AC = BC, If BC² = 2AC², prove that ABC is a right triangle.
Solution:
We have ∆ABC such that AB = AC

Also AB² = 2AC² = AC² + AC²
AB² = BC² +AC²(BC =AC given)
∠ACB = 90° (by converse of Pythagoras theorem)
i.e. ∆ABC is a right angle triangle

Question 6.
ABC is an equilateral triangle of side 2a. Find each of its attitudes.
Solution:
It is given that LABC is an equilateral triangle in which

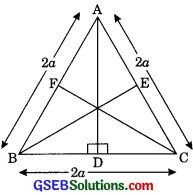
AB = AC = CB = 2a
Let us draw AD ⊥ BC
Now in ∆ABD and ∆ACD
AB = AC (Side of equilateral triangle)
AD = AD (Common)
∠ADB = ∠ADC (each 90°)
∴ ∆ABD ≅ ∆ACD (by RHS)
∴ BD = CD (by CPCT)
i.e. D is a mid point of BC
Hence BD = \(\frac {2a}{2}\) = a
Now in right ∆ABD
AB² = BD² + AD²
(2a)² = a² + AD²
4a² – a² = AD²
AD² = 3a²
AD = \(\sqrt { 3 } \)
Similarly BE = CF = \(\sqrt { 3 } \)

Question 7.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals. (CBSE 2012) of its diagonals. (CBSE 2012)
Solution:
Given: ABCD is a rhombus i.e. AB = BC = CD =
DA whose diagonals AC and BD intersect at O.
To prove: AC² + BD²
= AB² + BC² + CD² + DA²

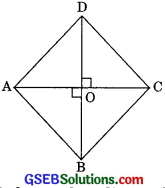
Proof: We know that diagonals of a rhombus bisect each other at right angles.
∴ OA = OC and OB = OD
Now in right ∆AOB
AB² = OA² + OB² (by Pythagoras theorem)
In right ∆BOC
BC² = OB² + OC²……..(2)
Similarly in ∆COD
CD² = OC² + OD²
and in right ∆AOD
AD² – OA² + OD²
Now adding eqn (1), (2), (3) and (4) we get
AB² + BC² + CD² + DA²
= OA² + OB² + OC² + OB² + OD² + OC² + OD² + OA²
= 20A² + 20B² + 20C² + 20D²
= 20A² + 20B² + 20A² + 20B²
= 40A² + 40B²
= (20A)² + (20B)² + AB² + BC² + CD² + DA²
= AC² + BD²
(20A = AC and 20B = BD)

Question 8.
In the figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB show that
(i) OA² + OB² + OC² – OD² – DE² – OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF²

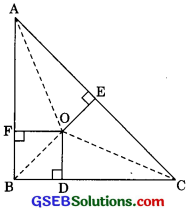
Solution:
In the given figure, 0 is in the interior of ∆ABC,
OD ⊥ BC, OF ⊥AB, OE ⊥AC
To prove:
(i) OA² + OB² + OC² + 0D² + 0E² + OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = 2 + CD² + BF²
Construction: Join OA, OB and OC
Proof: In right ∆AOF
OA² = AF² + OF² (by Pythagoras theorem)
AF² = OA² + OF² ……….(1)

In right ∆OBD
OB² + BD² + OD²
BD² = OB² + OD² ………..(2)

In right ∆OCE
OC² = CE² + OE²
CE² = OC² + OE²
Adding eqn (1), (2) and (3) we get
AF² + BD² + CE² = OA² + OB² + OC² + OD² + OE² – OF² ………..(3)

(ii) In right ∆OBD
OB² = OD² + BD²
(by Pythagoras theorem)
⇒ BD² = OB² – OD² ……….(1)

In right triangle ∆OCD
OC² = OD² + CD²
(by Pythagoras theorem)
⇒ CD² = OC² – OD² ……….(2)

Subtracting eqn (2) from eqn (1)
BD² – CD² = OB² – OD² – OC² – OD²
BD² – CD² = OB² – OC² ……….(3)
Similarly in right triangle OCE and OAE we get
CE² = OC² – OE² ………(4)
(by Pythagoras theorem)
AE² = OA² – OE² ………(5)

Subtracting eqn (5) from eqn (4)
CE² – AE² = OC² – OE² – OA² + OE²
⇒ CE² – AE² = OC² – OA² ……….(6)

And in right triangle OAF and OBF
AF² = OA² – OF² ……….(7)
BF² = OB² – OF² ………..(8)

Subtracting eqn (8) form (7)
AF² – BF² = AO² – OF² – OB² + OF²
2 – BF² = OA² – OB² ………..(9)

Adding eqn (3), (6) and eqn (9) we get
BD² + CE² + AF² – CD² – AE² – BF²
⇒ OB² + OC² + OA² – OC² – OA² – 0B²
BD² + CE² + AF² – CD² – AE² – BF² = O
BD² + CE² + AF² = CD² + AE² + BF²

Question 9.
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Solution:
Let AB is a ladder and A is the foot of the ladder BC is the wall.

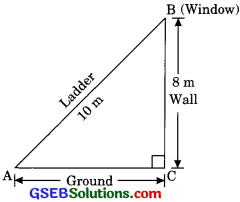
Now in right triangle ABC
AB² = AC² + BC²
(by Pythagoras theorem)
(10)² + AC² + 8²
⇒ 100 – 64 = AC²
⇒ AC² = 36
⇒ AC = 6m
Hence, the distance of the foot of the ladder from the base of wall is 6 m.

Question 10.
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a state attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut.
Solution:
Let AB is the wire and BC is the vertical pole. The point A is the stake.

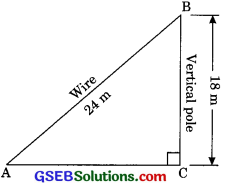
Now in right triangle ABC
AB² = AC² + BC²
24² = AC² + 18²
AC² = 24² – 18²
AC² = (24 – 18)(24 + 18)
AC² = 6 x 42
AC = \(\sqrt{6 \times 42}\)
AC = \(\sqrt{6 \times 6 \times 7}\)
⇒ AC = 6\(\sqrt{6 \times 42}\)m.

Question 11.
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two plane after 1 \(\frac{1}{2}\) hours?
Solution:
Let the point A represent the airport. First plane flies due North with speed of 1000 km/h.
Distance of plane after 1\(\frac{1}{2}\) hour from airport = speed x time

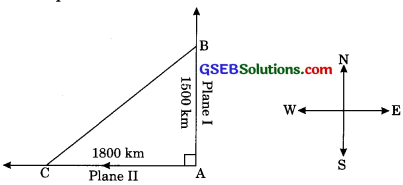
Distance due North = 1000 x 1\(\frac{1}{2}\)
= 1000 x \(\frac{3}{2}\)
= 1500 km
Similarly, distance of plane after 11\(\frac{1}{2}\) hour From airport due west
= 1200 x 11\(\frac{1}{2}\) = 1200 x \(\frac{3}{2}\)
= 1800 km
Hence in right triangle ABC
BC² = AB² + AC²
BC² = (1500)² + (1800)²
BC² = 22500 + 32400
BC² = 54900
BC = \(\sqrt{54900}\) km
BC = \(\sqrt{61 x 90000}\)
BC = 300 \(\sqrt{61}\)m.

Question 12.
Two poles of height 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Solution:
Let AB and CD be the two poles. Distance between their feet is 12 m. Height of pole 1st
AB = 11 m and height of pole lind CD = 6 m

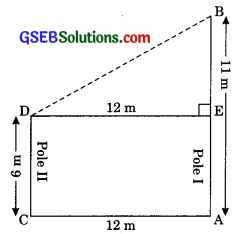
AB = 11m
CD = 6m
BB = AB – AE (AE = CD)
⇒BE =11 – 6
⇒BE = 5m

In ∆BED
BD² = DE² + BE²
= 12² + 5² = 144 + 25
⇒ BD² = 169
⇒ BD = 13m
Thus the distance between tops is 13 metres.

Question 13.
D and E are points on the sides CA and CB respectively of a triangle ABC, right angled at C. Prove that AE² + BD² = AB² + DE²
Solution:
Given: ∆ABC in which ∠C = 90°, D and E are the mid prints on the sides AC and BC.

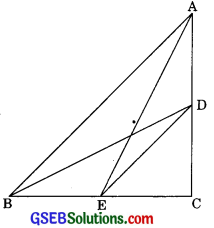
To prove: AB² + BD² = AB² + DE²
Proof: In right angle AACB
AB² = AC² + BC² (by Pythagoras theorem)
In DCE
DE² = CD² + CE² ………(2)
(by Pythagoras theorem)
Adding eqn (1) and (2)
We get AB² + DE² = AC² + BC² + CD² + CE²
AB² + DE² = (AC² + CE²) +(BC² + CD²) …….(3)

Now in ∆ACE
AE² = AC² + CE² ……. (4)
In ∆BCD
BC² + CD² = BD² ……(5)
from eqn (3), (4) and (5)
AB² + DE² = AE² + BD²

Question 14.
The perpendicular from A on side BC at D of a ¿ABC intersects BC at D such that DB = 3CD (see figure). Prove that 2AB² = 2AC² + BC².
Solution:
Given: ∆ABC such that AD ⊥ BC. The position of D is such that BD = 3 CD.

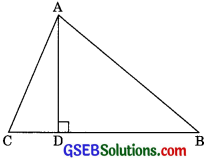
In right ∆ABD, we have
AB² = AD² + BD² …….(1) (by Pythagoras theorem)
Similarly from right IACD,
AC² = AD² + CD² ……(2)
Note that, BC = DB + CD
BC = 3CD + CD (BD = CD given)
BC = 4 CD
Subtracting eqn (2) from eqn (1), we get
⇒ AB² – AC² = BD² – CD²
⇒ AB² – AC² = (BD + CD) (BD – CD)
⇒ AB² – AC² = BC (3CD – CD)
⇒ AB² – AC² = BC x 2CD
⇒ AB² – AC² = BC x \(\frac{2 \times \mathrm{BC}}{4}{r}\) CD = \(\frac{BC}{4}\)
⇒ AB² – AC² = \(\frac{\mathrm{BC} \times \mathrm{BC}}{2}\)
⇒ 2AB² – 2AC² = BC²
⇒ AB² = 2AC² + BC²

Question 15.
In an equilateral triangle ABC, D is a point on side BC such that BD = BC. Prove that
Solution:
Given: AABC is an equilateral triangle.

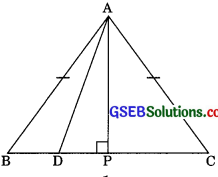
BD = \(\frac{1}{3}\) BC
To prove: 9AD² = 7AB²
Construction: Draw AP⊥BC
Proof: In right AAPB, we have
AB² =AP² + BP² …….(1) (by Pythagoras theorem))
Now, in right triangle APD, we have
AD² = AP² + DP²
(by Pythagoras theorem)
AP² =AD² – DP²
From eqn (1) and (2) we get
AB² =AD² – DP² + BP²
AB² =AD² – DP² + (BP = BC)
AD² = AB² + DP² – 4
Note that, DP = BP – BD
DP = \(\frac{1}{2}\)BC – \(\frac{1}{3}\)BC = \(\frac{1}{6}\)BC in (3),gives
Substituting value of DP = \(\frac{1}{6}\)BC
AD² = AB² + (\(\frac{1}{6}\)BC²)² – \(\frac{\mathrm{BC}^{2}}{4}\)
⇒ AD² = AB² + \(\frac{\mathrm{BC}^{2}}{36}\) – \(\frac{\mathrm{BC}^{2}}{4}\)
⇒ AD² = AB² + \(\frac{\mathrm{BC}^{2}-9 \mathrm{BC}^{2}}{36}\)
⇒ AD² = AB² – \(\frac{8 \mathrm{BC}^{2}}{36}\)
⇒ AD² = AB² – \(\frac{2 \mathrm{BC}^{2}}{9}\)
⇒ AD² = AB² – \(\frac{2 \mathrm{2AB}^{2}}{9}\) (BC = AB = AC)
⇒ 9AD² = 9AB² – 2AB²
⇒ 9AD² – 7AB²

Question 16.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitude.
Solution:
Given: ABC is an equilateral triangle,
To Prove: 3AB² = 4AD²

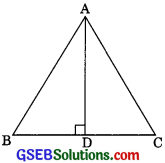
Construction: Draw AD ⊥BC
Proof In right ∆ADB
BD = DC = \(\frac{BC}{2}\) ………(1) (D is the midpoint)
AB² = AD² + BD²
AB² = AD² + \(\left(\frac{\mathrm{BC}}{2}\right)^{2}\)[(Using (1)]
AB² = AD² + \(\frac{\mathrm{BC}^{2}}{4}\) (∆ABC is an equilateral)
= AB² = AD² + \(\frac{\mathrm{AB}^{2}}{4}\) (asAB = BC)
4AB² = 4AD² + AB²
3AB² = 4AD²

Question 17.
Tick the correct answer and justify: In AB = 6\(\sqrt {3} \) cm, AC = 12 cm, and BC = 6 cm. The angle B is
(a) 120°
(b) 60°
(c) 90°
(d) 45°
Solution:
Wehave AB = 6\(\sqrt {3} \) cm,AC = 12cm, and BC = 6 cm
AB² = (6\(\sqrt {3} \))² = 36 x 3
AB² = 108
AC² = 122 = 144
BC² = ² = 36
Since 144 = 108 + 36
i.e. AC² = AB² + BC²
Hence the given triangle is right angle triangle at B
∠B = 90°
∴ The correct answer is (c).