Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 1 Sets Ex 1.5 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 1 Sets Ex 1.5
Question 1.
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, B = {2, 4, 6, 8}, C = {3, 4, 5, 6}
Find:
(i) A’
(ii) B’
(iii) (A ∪ C)’
(iv) (A ∪ B)’
(v) (A’)’
(vi) (B – C)’
Solution:
(i) A’ = U – A = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4}
= {5, 6, 7, 8, 9}.
(ii) B’ = (1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 4, 6, 8}
= {1, 3, 5, 7, 9}.
(iii) A ∪ C = {1, 2, 3, 4} ∪ {3, 4, 5, 6} = {1, 2, 3, 4, 5, 6}
∴ (A ∪ C)’ = (1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 5, 6} = {7, 8, 9}.
(iv) A ∪ B = {1, 2, 3, 4} ∪ {2, 4, 6,8} = {1, 2, 3, 4, 6, 8}.
∴ (A ∪ B)’ = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 6, 8} = {5, 7, 9}
(v) A’ = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 6, 8}
(A’)’ = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4} = {5, 6, 7, 8, 9}
= {1, 2, 3, 4}.
(vi) B – C = {2, 4, 6, 8} – {3, 4, 5, 6} = {2, 8}
(B – C)’ = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 8}
= {1, 3, 4, 5, 6, 7, 9}.
![]()
Question 2.
If U = {a, b, c, d, e, f, g, h}, find the complements of the following sets:
A = {a, b, c}, B = {d, e, f, g}, C = {a, c, e, g}, D = {f, g, h, a}
Solution:
(i) A’ = U – A = {a, b, c, d, e, f, g, h} – {a, b, c} = {d, e, f, g, h).
(ii) B’ = {a, b, c, d, e, f, g, h} – {d, e, f, g} = {a, b, c, h}.
(iii) C’ = {a, b, c, d, e, f, g, h} – {a, c, e, g} = {b, d, f, h}.
(iv) D’ = {a, b, c, d, e, f, g, h} – {f, g, h, a} = {b, c, d, e}.
Question 3.
Taking the set of natural numbers as universal set, write down the complements of the following sets:
- {x : x is an even number}
- {x : x is an odd number}
- {x : x is a positive multiple of 3}
- {x : x is a prime number}
- {x : x is a natural number divisible by 3 and 5}
- {x : x is a perfect square}
- (x : x is a perfect cube}
- {a : x + 5 = 8}
- {x : 2x + 5 = 9}
- {x : x ≥ 7}
- {x : x ∈ N and 2x + 1 > 10}
Solution:
- {x : x is an odd natural number}
- {x : x is an even natural number}
- {x : x ∈ N and x is not a multiple of 3}
- {x : x is a composite number or x = 1}
- {x : x ∈ N and x is neither divisible by 3, nor by 5}
- {x : x ∈ N, and x is not a perfect square}
- {x : x ∈ N and x is not a perfect cube}
- {x : x ∈ N, and x ≠ 3}
- {x : x ∈ N, and x ≠ 2}
- {x : x ∈ N, and x < 7}
- {x : x ∈ N and x ≤ \(\frac{9}{2}\)}
![]()
Question 4.
If U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 6, 8}, B = {2, 3, 5, 7}. Verify that:
(i) (A ∪ B)’ = A’ ∩ B ‘
(ii) (A ∩ B)’ = A’ ∪ B’
Solution:
(i) A ∪ B = {2, 4, 6, 8} ∪ {2, 3, 5, 7} = {2, 3, 4, 5, 6, 7, 8}
(A ∪ B)’ = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 3, 4, 5, 6, 7, 8} = {1, 9}
A’ = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 4, 6, 8}
= {1, 3, 5, 7, 9}
B’ = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 3, 5, 7} = {1, 4, 6, 8, 9}
A’ ∩ B’ = {1, 3, 5, 7, 9} ∩ {1, 4, 6, 8, 9} = {1, 9}.
∴ (A ∪ B)’ = A’ ∩ B’.
(ii) A ∩ B = {2, 4, 6, 8} ∩ {2, 3, 5, 7} = {2} .
(A ∩ B)’ = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2} = {1, 3, 4, 5, 6, 7, 8, 9}
A’ ∪ B’ = {1, 3, 5, 7, 9} ∪ {1, 4, 6, 8, 9}
= {1, 3, 4, 5, 6, 7, 8, 9}.
Hence, (A ∩ B)’ = A’ ∪ B’.
Question 5.
Draw appropriate Venn diagram for each of the following:
- (A ∪ B)’
- A’ ∩ B’
- (A ∩ B)’
- A’ ∪ B’
Solution:
1. Shaded Area (A ∪ B)’
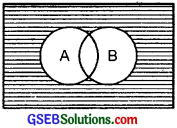
2. A’ ∩ B’ = Common shaded area

3. (A ∩ B)’ = shaded area
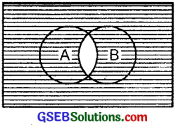
4. A’ ∪ B’ = All shaded area formed by all horizontal and vertical lines.

![]()
Question 6.
Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60°, what is A’?
Solution:
A is the set of triangles in which no triangle is equilateral.
∴ A’ = set of equilateral triangles.
Question 7.
Fill in the blanks to make each of the following a true statement:
- A ∪ A’ = …………………….
- ϕ’ ∩ A = …………………….
- A ∩ A’ = ………………….
- U’ ∩ A = …………………..
Solution:
Let U be the universal set.
- A ∪ A’ = U
- ϕ’ ∩ A = U ∩ A = A
- A ∩ A’ = ϕ
- U’ ∩ A = ϕ ∩ A = ϕ