Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 11 Conic Sections Ex 11.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 11 Conic Sections Ex 11.2
In each of the following questions 1 to 6, find the co-ordinates of the focus, axis of the parabola, the equation of the directrix and length of latus rectum:
Solutions to questions 1-6:
1. y2 = 12x
2. x2 = 6y
3. y2 = – 8x
4. x2 = – 16y
5. y2 = 10x
6. x2 = – 9y
Solutions to questions 1-6:
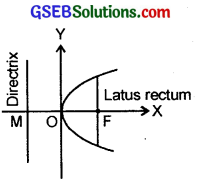
1. y2 = 12x is the equation of parabola.
So, 4a = 12 ⇒ a = 3.
∴ Focus (3, 0)
Axis is x-axis, i.e., y = 0.
Directrix is x = – 3.
Length of latus rectum = 4a = 12.
![]()
2. x2 = 6y is the equation of parabola.
∴ 4a = 6.
∴ a = \(\frac{6}{4}\) = \(\frac{3}{2}\).
Focus (0, \(\frac{3}{2}\)).
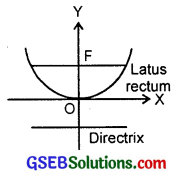
Axis is y-axis i.e., x = 0.
Directrix is y = – \(\frac{3}{2}\).
Length of latus rectum = 6.
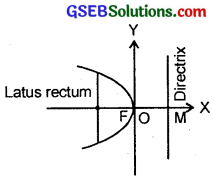
3. y2 = – 8x is the equation of parabola.
∴ 4a = 8, ⇒ a = 2.
Focus (- 2, 0).
Axis is x-axis y = 0.
Latus rectum Directrix is x = 2.
Length of latus rectum = 4a = 8.
![]()
4. x2 = – 16y is the equation of parabola.
∴ 4a = 16 ⇒ a = 4.
Focus (0, – 4).
Axis is y-axis, x = 0.
Directrix is y = 4.
Length of latus rectum = 16.
5. y2 = 10x is the equation of parabola.
∴ 4a = 10 ⇒ a = \(\frac{5}{2}\).
Focus (\(\frac{5}{2}\), 0).
Axis is x-axis, i.e., y = 0.
Directrix is x = – \(\frac{5}{2}\).
Length of latus rectum = 10.
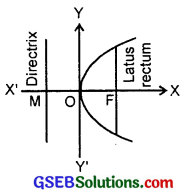
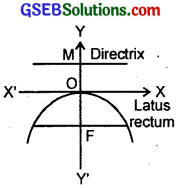
6. Equation of parabola is
x2 = – 9y, (see fig. 4)
∴ 4a = 9 ⇒ a = \(\frac{9}{4}\).
Focus (0, – \(\frac{9}{4}\)).
Axis of parabola is y-axis i.e., x = 0.
Directrix is y = \(\frac{9}{4}\).
Length of latus rectum = 9.
![]()
In each of the following questions 7 to 12, find equation of the parabola that satisfies the given conditions:
7. Focus is (6, 0) and directrix is x = – 6.
8. Focus is (0, – 3), dlrectrix y = 3.
9. Vertex (0, 0) and Focus (3, 0).
10. Vertex (0, 0) and Focus (- 2, 0).
11. Vertex (0, 0), passing through (2, 3) and axis is along x-axis.
12. Vertex (0, 0), passing through (5, 2) and symmetric with respect to y-axis.
Solutions to questions 7-12:
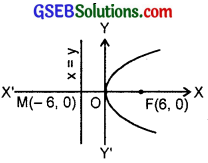
7. Focus is (6, 0) and directrix is x = – 6. Its vertex is the mid-point of (6, 0) and (- 6, 0).
∴ Vertex = (0, 0)
∴ a = 6 and so equation of parabola is y2 = 24x.
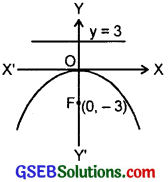
8. Focus (0, – 3), directrix is y = 3.
Vertex is the mid-point of (0, – 3) and (0, 3).
i.e., vertex is (0, 0)
and a = 3 ⇒ 4a = 12.
∴ Equation of parabola is x2 = – 12y.
![]()
9. Vertex (0, 0), focus is (3, 0).
So, a = 3 ⇒ 4a = 12.
∴ Equation of parabola is y2 = 12x.
10. Vertex (0, 0), focus (- 2, 0).
a = 2, focus being (- 2, 0). It is directed towards OX’.
∴ Equation of parabola is y2 = – 8x.
11. Vertex (0, 0). Parabola passes through (5, 2)
Axis of parabola is x-axis.
Let the equation of parabola be y2 = 4ax.
It passes through (2, 3).
∴ 9 = 4.a.2
∴ a = \(\frac{9}{8}\).
∴ Equation of parabola is y2 = \(\frac{9}{2}\)x or 2y2 = 9x.
![]()
12. Vertex (0, 0). Parabola passes through (5, 2).
It is symmetric about y-axis.
Let the equation of parabola be x2 = 4ay.
(5, 2) lies on it.
∴ 25 = 4a.2. ⇒ a = \(\frac{25}{8}\).
∴ Equation of parabola is x2 = \(\frac{25}{2}\)y or 2x2 = 25y.