Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 11 Conic Sections Ex 11.4 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 11 Conic Sections Ex 11.4
In each of the following questions 1 to 6, find the co-ordinates of the foci and the vertices, the eccentricity and length of latus rectum of the hyperbola:
1. \(\frac{x^{2}}{16}\) – \(\frac{y^{2}}{9}\) = 1
2. \(\frac{y^{2}}{9}\) – \(\frac{x^{2}}{27}\) = 1
3. 9y2 – 4x2 = 36
4. 16x2 – 9y2 = 576
5. 5y2 – 9x2 = 36
6. 49y2 – 16x2 = 784
Solutions to questions 1-6:
1. Equation of the hyperbola is
\(\frac{x^{2}}{16}\) – \(\frac{y^{2}}{9}\) = 1
Here, a2 = 16 ⇒ a = 4, b2 = 9 ⇒ b = 3.
∴ c2 = a2 + b2 = 16 + 9 = 25.
∴ c = 5.
Axis is x-axis.
Co-ordinates of foci (± 5, 0).
Co-ordinates of vertices (± 4, 0).
Eccentricity e = \(\frac{c}{a}\) = \(\frac{5}{4}\).
Latus rectum = \(\frac{2b^{2}}{a}\) = \(\frac{2×9}{4}\) = \(\frac{9}{2}\).
![]()
2. Equation of hyperbola is \(\frac{y^{2}}{9}\) – \(\frac{x^{2}}{27}\) = 1.
Here, a2 = 9, b2 = 27,
⇒ c2 = a2 + b2
= 9 + 27 = 36.
a = 3,b = 3\(\sqrt{3}\), c = 6.
Axis of hyperbola is y-axis.
∴ Foci are 5(0, ± 6).
Vertices (0, ± 3)
Eccentricity e = \(\frac{c}{a}\) = \(\frac{6}{3}\) = 2.
Latus rectum = \(\frac{2b^{2}}{a}\) = \(\frac{2×27}{3}\) = 18.
3. 9y2 – 4x2 = 36 is the equation of hyperbola.
i.e; \(\frac{y^{2}}{4}\) – \(\frac{x^{2}}{9}\) = 1.
a2 = 4, b2 = 9, c2 = a2 + b2 = 4 + 9 = 13.
∴ a = 2, b = 3, c = \(\sqrt{3}\).
Axis is y-axis.
Foci (0, ± \(\sqrt{13}\)), vertices (0, ± 2).
Eccentricity e = \(\frac{c}{a}\) = \(\frac{10}{6}\) = \(\frac{5}{3}\).
Latus rectum = \(\frac{2b^{2}}{a}\) = \(\frac{2×64}{6}\) = \(\frac{64}{3}\).
![]()
5. Equation of hyperbola is 5y2 – 9x2 = 36.

Axis is along y-axis.

6. Equation of hyperbola is 49y2 – 16x2 = 784.
or \(\frac{y^{2}}{16}\) – \(\frac{x^{2}}{49}\) = 1.
∴ a2 = 16, b2 = 49, c2 = 16 + 49 = 65.
⇒ a = 4, 5 = 7, c = \(\sqrt{65}\).
Axis is y-axis.
Foci are (0, ± \(\sqrt{65}\)) and vertices are (0, ± 4).
Eccentricity e = \(\frac{c}{a}\) = \(\frac{\sqrt{65}}{4}\),
latus rectum = \(\frac{2b^{2}}{a}\) = \(\frac{2×49}{4}\) = \(\frac{49}{2}\).
In each of the following questions 7 to 15, find the equations of hyperbola satisfying the given conditions:
7. Vertices (± 2,0), foci (± 3, 0)
8. Vertices (0, ± 5), foci (0, ± 8)
9. Vertices (0, ± 3), foci (0, ± 5)
10. Foci (± 5, 0), the transverse axis is of length 8.
11. Foci (0, ± 13), the conjugate axis is of length 24.
12. Foci (± 3\(\sqrt{5}\), 0), the latus rectum is length 8.
13. Foci (± 4, 0), the latus rectum is of length 12.
14. Vertices (± 4, 0), e = \(\frac{4}{3}\).
15. Foci (0, ± \(\sqrt{10}\)), passing through (2, 3).
Solutions to questions 7-15:
7. We have: vertices (± 2, 0) and foci (± 3, 0).
Axis of hyperbola is x-axis.
a = 2, c = 3 ⇒ b2 = c2 – a2 = 9 – 4 = 5.
∴ b = \(\sqrt{5}\).
Equation of hyperbola is
\(\frac{x^{2}}{4}\) – \(\frac{y^{2}}{5}\) = 1.
![]()
8. The given vertices are (0, ± 5), which lie on y-axis.
Thus, equation of the hyperbola is of the form
\(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}\) = 1
The vertices of hyperbola (1) are (0, ± a). Here, the vertices are given to be (0, ± 5).
∴ a = 5.
The co-ordinates of foci of (1) are (0, ± ae). Here, they are given to be (0, ± 8).
So, ae = 8 ⇒ 5e = 8 ⇒ e = \(\frac{8}{5}\).
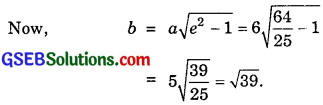
Hence, the required equation of the hyperbola is
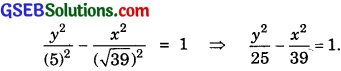
9. Vertices are (0, ± 3) ⇒ a = 3.
Foci are (0, ± 5) ⇒ c = 5.
So, b2 = c2 – a2
= 25 – 9 = 16
⇒ b = 4.
∴ Equation of hyperbola is (axis being y-axis):
\(\frac{y^{2}}{9}\) – \(\frac{x^{2}}{16}\) = 1.
![]()
10. Foci are (± 5, 0) ⇒ c = 5.
Transverse axis = 8 ⇒ a = 4.
∴ b2 = c2 – a2
= 25 – 16 = 9
⇒ b = 3.
Axis of hyperbola is x-axis, since (± 5, 0) lies on it. Therefore, equation of the hyperbola is
\(\frac{x^{2}}{16}\) – \(\frac{y^{2}}{9}\) = 1.
11. Foci are (0, ± 13) ⇒ c = 13.
The length of conjugate axis = 26 = 24 ⇒ b = 12.
a2 = c2 – b2
= 169 – 144
= 25
⇒ a = 5
Axis of hyperbola is y-axis, since (0, ± 13) lies on it.
\(\frac{y^{2}}{25}\) – \(\frac{x^{2}}{144}\) = 1.
![]()
12. Foci are (± 3\(\sqrt{5}\), 0) ⇒ c = 3\(\sqrt{5}\).
The length of latus rectum = \(\frac{2b^{2}}{a}\) = 8.
∴ b2 = 4a ……………… (1)
Also, c2 = a2 + b2 i.e., 45 = a2 + b2 …………………. (2)
Eliminating, from (1) and (2), we get
45 = a2 + 4a or a2 + 4a – 45 = 0.
or (a + 9)(a – 5) = 0.
a ≠ – 9 ∴a = 5 ⇒ b2 = 4a = 4 × 5 = 20.
a2 = 25 and b2 = 20
∴ Equation of hyperbola is [Since (± 3\(\sqrt{5}\), 0) lies on x-axis]
\(\frac{x^{2}}{25}\) – \(\frac{y^{2}}{20}\) = 1.
13. Foci are (± 4, 0) ⇒ c = 4
or c2 = a2 + b2 ⇒ 16 = a2 + b2 ……………. (1)
∴ Latus rectum = \(\frac{2b^{2}}{a}\) = 12.
∴ b2 = 6a ……………. (2)
Eliminating b2 from (1) and (2), we get
∴ 16 = a2 + 6a or a2 + 6a – 16 = 0.
or (a + 8)(a – 2) = 0 [∵a ≠ – 8]
∴ a = 2 ⇒ b2 = 6a = 6 × 2 = 12.
∴ a2 = 4, b = 12, Axis is x-axis.
So, equation of the hyperbola is
\(\frac{x^{2}}{4}\) – \(\frac{y^{2}}{12}\) = 1.
![]()
14. Vertices are (± 7, 0) ⇒ a = 7.

Axis is along x-axis.
So, equation of the hyperbola is
\(\frac{x^{2}}{49}\) – \(\frac{y^{2}}{343/9}\) = 1 or 7x2 – 9y2 = 343.
15. The given foci are (0, ± \(\sqrt{10}\)), which lies on y-axis.
Let the equation of hyperbola be
\(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}\) = 1.
∴ ae = \(\sqrt{10}\).
Also, b2 = a2(e2 – 1) = a2e2 – a2.
= 10 – a2. ………………….. (2)
Thus, the equation of the hyperbola is
\(\frac{y^{2}}{a^{2}}\) – \(\frac{x^{2}}{10-a^{2}}\) = 1.
As it passes through the point (2, 3), so
= \(\frac{9}{a^{2}}\) – \(\frac{4}{10-a^{2}}\) = 1 ⇒ 90 – 9a2 – 4a2 = a2(10 – a2)
⇒ a4 – 23a2 + 90 = 0 ⇒ (a2 – 5)(a2 – 18) = 0.
⇒ a2 = 18, 5.
When a2 = 18, then from (2), b2 = – 8, which is not possible and when a2 = 5, then from (2), b2 = 5.
Hence, the required equation of the hyperbola is
\(\frac{y^{2}}{5}\) = \(\frac{x^{2}}{5}\) = 1 ⇒ y2 – x2 = 5.