Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 12 Introduction to three Dimensional Geometry Ex 12.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 12 Introduction to three Dimensional Geometry Ex 12.2
Question 1.
Find the distance between the following pairs of points:
(i) (2, 3, 5), (4, 3, 1)
(ii) (- 3, 7, 2), (2, 4, – 1)
(iii) (-1, 3, – 4), (1, – 3, 4)
(iv) (2, – 1, 3), (- 2, 1, 3).
Solution:
(i) The given points are (2, 3, 5) and (4, 3, 1).

![]()
Question 2.
Show that the points (- 2, 3, 5), (1, 2, 3) and (7, 0, – 1) are collinear.
Solution:
Let the given points be A(- 2, 3, 5), B(0, 2, 3) and C(7, 0, – 1).

Now, AB + BC = \(\sqrt{14}\) + 2\(\sqrt{14}\) = 3\(\sqrt{14}\).
Thus, AB + BC = AC.
Hence, the points A, B and C are collinear.
![]()
Question 3.
Verify the following:
(i) (0, 7, – 10), (1, 6, – 6) and (4, 9, – 6) are the vertices of an isosceles triangle.
(ii) (0, 7, 10), (- 1, 6, 6) and (- 4, 9, 6) are the vertices of a right angled triangle.
(iii) (- 1, 2, 1), (1, – 2, 5), (4, – 7, 8) and (2, – 3, 4) are the vertices of a parallelogram.
Solution:
(i) Let A(0, 7, – 10), B(1, 6, – 6) and C(4, 9, – 6) donate the given points. Then,
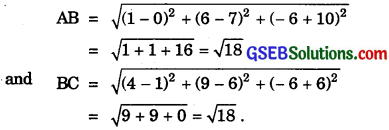
∴ AB = BC
Thus, the ∆ABC is isosceles.
(ii) Let A(0, 7, 10), B(- 1, 6, 6) and C(- 4, 9, 6) denote the given points. Then,

Now, AB2 + BC2 = (3\(\sqrt{2}\))2 + (3\(\sqrt{2}\))2
= 18 + 18 = 36.
Also, AC2 = 36.
∴ AB2 + BC2 = AC2
⇒ ABC is right ∠d triangle with ∠B = 90°.
(iii) The given points are A(- 1, 2, 1), B(1, – 2, 5), C(4, – 7, 8) and D(2, – 3, 4). Then, by distance formula,

Now, AB = CD and BC = DA, i.e., opposite sides are equal and AC ≠ BD, i.e., the diagonals are not equal.
So, ABCD is a parallelogram.
![]()
Question 4.
Find the equation of the set of points P, which are equidistant from (1, 2, 3) and (3, 2, – 1).
Solution:
Let A(1, 2, 3) and B(3, 2, – 1) be the given points and the coordinates of points P be (x, y, z).
We are given AP = BP
or AP2 = BP2
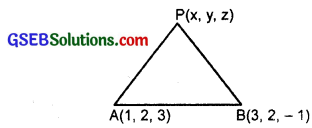
∴ (x – 1)2 + (y – 2)2 + (z – 3)2 = (x – 3)2 + (y – 2)2 + (z + 1)2
or x2 + y2 + z2 – 2x – 4y – 6z + 1 + 4 + 9
= x2 + y2 + z2 – 6x – 4y + 2z + 9 + 4 + 1
or – 2x – 4y – 6z = – 6x – 4y + 2z
or 4x – 8z = 0
or x – 2z = 0.
![]()
Question 5.
Find the equation of set of points P, the sum of whose distances from A(4, 0, 0) and B(- 4, 0, 0) is equal to 10.
Solution:
The given points are A(4, 0, 0) and B(- 4, 0, 0).
Let the point P be (x, y, z).
We have:
PA + PB = 10.
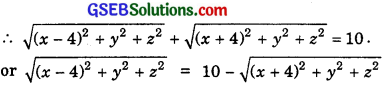
Squaring both sides, we get
(x – 4)2 + y2 + z2 = 100 + (x + 4)2 + y2 + z2 – 20 \(\sqrt{(x+4)^{2}+y^{2}+z^{2}}\)

Squaring again, we get
16x2 + 200x + 625 = 25(x2 + y2 + z2 + 8x + 16)
or 9x2 + 25y2 + 25z2
= 625 – 400
= 225
i.e., 9x2 + 25y2 + 25z2 = 225.