GSEB Solutions Class 11 Maths Chapter 15 Statistics Ex 15.1

Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 15 Statistics Ex 15.1 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 15 Statistics Ex 15.1

Find the mean deviation about the mean for the data in questions 1 and 2:
1. 4, 7, 8, 9, 10, 12, 13, 17
2. 38, 70, 48, 40, 42, 55, 63, 46, 54, 44
Solutions to questions 1 and 2:
1. Arithmetic mean \(\bar{x}\) of 4, 7, 8, 9, 10, 12, 13, 17 is
\(\bar{x}\) = \(\frac{4+7+8+9+10+12+13+17}{8}\) = \(\frac{80}{8}\)
= 10.
Σ |x_i – \(\bar{x}\)| = 6 + 3 + 2 + 1 + 0 + 2 + 3 + 7
= 24.
∴ Mean deviation about mean
= M.D. (\(\bar{x}\)) = \(\frac{\Sigma\left|x_{i}-\bar{x}\right|}{n}\) = \(\frac{24}{8}\) = 3.

2. Mean of the given data in

= 8.4

Find the mean deviation about the mean for the data in questions 3 and 4:
3. 13, 17, 16, 14, 11, 13, 10, 16, 11, 18, 12, 17.
4. 36, 72, 46, 42, 60, 45, 53, 46, 51, 49.
Solutions to questions 3 and 4:
3. The given data is
13, 17, 16, 14, 11, 13, 10, 16, 11, 18, 12, 17.

Arranging it in ascending order:
10, 11, 11, 12, 13, 13, 14, 16, 16, 17, 17, 18.
There are 12 observations.
∴ \(\frac{12}{2}\) th item = 6th item = 13.
and (\(\frac{12}{2}\) + 1)th item = 7th item = 14.
∴ Median M = \(\frac{1}{2}\)(13 + 14) = 13.5.
∴ \(\sum_{i=1}^{12}\)|x_i – M| = 3.5 + 2.5 + 2.5 + 1.5 + 0.5 + 0.5 + 0.5 + 2.5 + 2.5 + 3.5 + 3.5 + 4.5
= 28.
M.D. (M) = \(\frac{28}{12}\) = 2.33.

4. The given data is
36, 72, 46, 42, 60, 45, 53, 46, 51, 49.

Arranging the data in ascending order:
36, 42, 45, 46, 46, 49, 51, 53, 60, 72.
The number of observations = 10.
∴ \(\frac{10}{2}\)th = 5th observation = 46.
(\(\frac{10}{2}\) + 1)th = 6th observation = 49.
∴ Median = \(\frac{1}{2}\)(46 + 49) = 47.5.
= |36 – 47.51 + |42 – 47.5| + |45 – 47.5| + |46 – 47.5| + |46 – 47.5| + |49 – 47.5| + |51 – 47.5| + |53 – 47.5| + |60 – 47.5| + |72 – 47.5|
=11.5 + 5.5 + 2.5 + 1.5 + 1.5 + 1.5 + 3.5 + 5.5 + 12.5 + 24.5 = 70.
Deviations about median
∴ M.D.(M) = \(\frac{70}{10}\) = 7.

Find the mean deviation about the median for the data in questions 7 to 8:

Solutions to questions 7 and 8:
7. The table to find cumulative frequency c.f. and median is as follows:

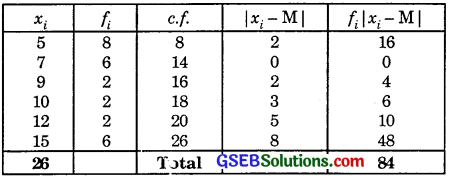
Total of the frequencies = 26.
∴Median M = \(\frac{1}{2}\)[\(\frac{26}{2}\)th value + (\(\frac{26}{2}\) + 1)th value]
= \(\frac{1}{2}\)(13th value + 14th value)
= \(\frac{1}{2}\)(7 + 7) = 7.
∴ Mean deviation from the median
\(\frac{\Sigma f_{i}\left(x_{i}-M\right)}{\Sigma f_{i}}\) = \(\frac{84}{26}\) = \(\frac{42}{13}\) = 3.23.

8. Cumulative frequency distribution of the given data is:

Since N = Σf_i = 29, which is odd, the median is the (\(\frac{n+1}{2}\))th observation, i.e., (\(\frac{29+1}{2}\) = 15)th observation, which is equal to 30. Thus, median is 30.
∴ Mean deviation from the median = \(\frac{\Sigma f_{i}\left|x_{i}-30\right|}{\Sigma f_{i}}\) = \(\frac{148}{29}\) = 5.1.

Find the median deviation about mean for the data in questions 9 and 10:

Solutions to questions 9 and 10:
9.

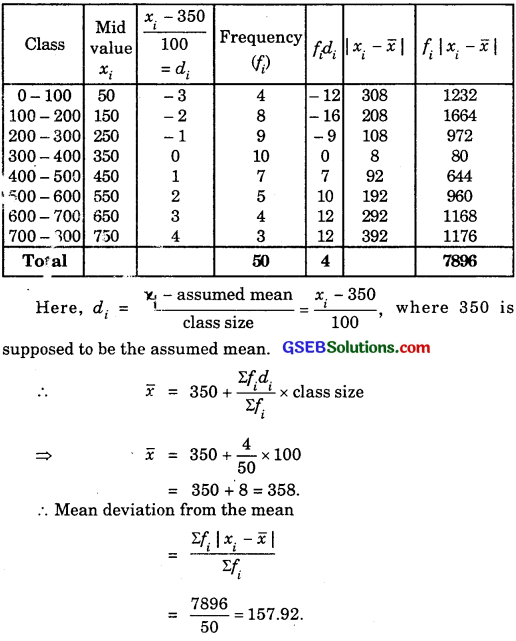
10.

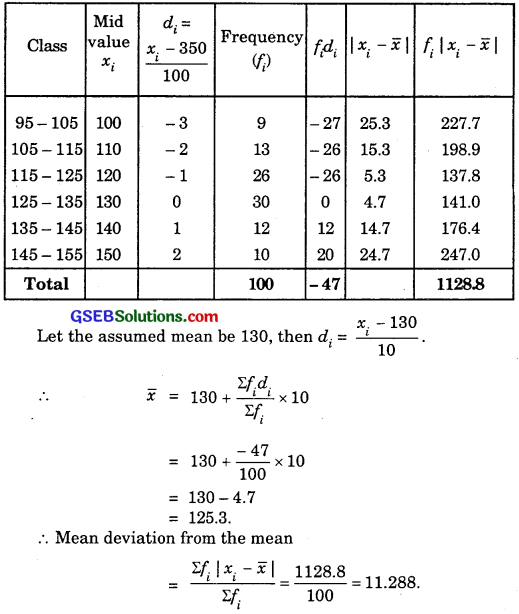
Question 11.
Find the mean deviation about median for the following data:

Solution:
Table to find cumulative frequencies and Σf_i|x_i – M| is given below:

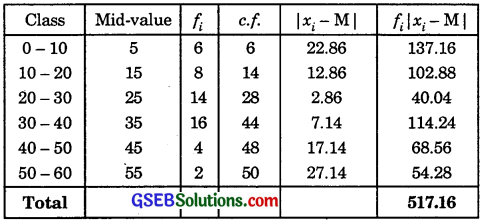
Here, \(\frac{N}{2}\) = \(\frac{50}{2}\) = 25.
So, median class is 20 – 30
∴ l = 20, f = 14, h = 10.
Median = \(\frac{\frac{N}{2}-C}{f}\) × h
= 20 + \(\frac{25-14}{14}\) × 10
= 20 + \(\frac{11}{14}\) × 10
= 20 + 7.86
= 27.86.
Σf_i|x_i – M| = 517.16.
∴ Median deviation about median
= \(\frac{517.16}{50}\) = 10.34

Question 12.
Calculate the mean deviation about median for the age distribution of 100 persons given below:

Solution:
Continuous frequency distribution, cumulative frequencies and f_i|x_i – M| are given in the following table:

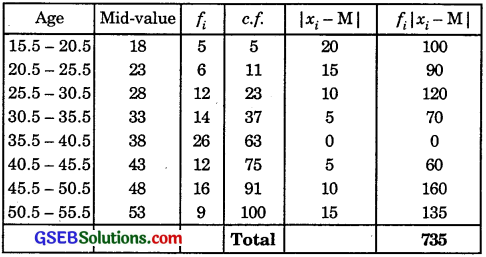
Median class 35.5 – 40.5.
∴ l = 35.5 and h = 5, C = 37, f = 26.
∴ Median = l + \(\frac{\frac{N}{2}-C}{f}\) × h
= 35.5 + \(\frac{50-37}{26}\) × 5 = 35.5 + \(\frac{13}{26}\) × 5
= 35.5 + 2.5 = 38.
∴ Σf_i|x_i – M| = 735..
N = Σf_i = 100.
Mean deviation about Median
= \(\frac{\Sigma f_{i}\left|x_{i}-M\right|}{N}\) = \(\frac{735}{100}\) = 7.35.