GSEB Solutions Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.1

Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.1 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.1

Question 1.
Find the radian measures corresponding to the following degree measures?

1. 25°
2. – 47°30′
3. 240°
4. 520°

Solution:
1. We have:
180° = π radians
∴ 25° = \(\frac{π}{180}\) × 25 radians = \(\frac{5π}{36}\) radians.

2. 60′ = 1°
∴ 30′ = \(\frac{30°}{60}\) = \(\frac{1°}{2}\)
∴ 47°30′ = (47 + \(\frac{1}{2}\)) degrees = \(\frac{95}{2}\) degrees
Now, 180° = π radians
So, – \(\frac{95°}{2}\) = \(\frac{- π}{180}\) × \(\frac{95}{2}\) radians = \(\frac{- 19π}{72}\) radians.

3. 180° = π radians.
∴ 240° = \(\frac{π}{180}\) × 240 radians
= \(\frac{4π}{3}\) radians.

4. 180° = π radians
∴ 520° = \(\frac{π}{180}\) × 520 radians = \(\frac{26π}{9}\) radians.

Question 2.
Find the degree measures corresponding to the following radian measures. [Use π = \(\frac{22}{7}\)]
(i) \(\frac{11}{16}\)
(ii) – 4
(iii) \(\frac{5π}{3}\)
(iv) \(\frac{7π}{6}\)
Solution:
(i) π radians = \(\frac{22}{7}\) radians = 180°
∴ \(\frac{11}{16}\) radians = \(\frac{180}{22}\) × 7 × \(\frac{11}{16}\) degree
= \(\frac{315}{8}\) degrees = 39 \(\frac{3}{8}\) degrees
= 39°22’30”.
Note: \(\frac{3°}{8}\) = \(\frac{3}{8}\) × 60′ = \(\frac{45}{2}\) = 22’30”.

(ii)

(iii) \(\frac{5π}{3}\) = \(\frac{5}{3}\) × 180° = 300°.

(iv) \(\frac{7π}{6}\) = \(\frac{7}{6}\) × 180° = 210°.

Question 3.
A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Solution:
Angle rotated in one revolution = 2π radians
∴ Angle rotated in 360 revolutions = 360 × 2π radians
⇒ Angle turned in one minute or 60 sec = 360 × 2π.
Hence, angle turned in 1 sec = \(\frac{360 × 2π}{60}\).
= 12π radians.

Question 4.
Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm. (Use π = \(\frac{22}{7}\))
Solution:
We know that:
l = rθ,
where l = length of arc = 20 cm,
r = radius of circle = 100 cm
and θ = angle subtended at the centre

Question 5.
In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of the minor arc corresponding to the chord?
Solution:
Since radius = length of chord = 20 cm, so
∆ OAB is equilateral triangle
⇒ θ = 60°.
Now, l = rθ
So, l = 20 × 60° × \(\frac{π}{180°}\) = \(\frac{20π}{3}\)
Thus, l = \(\frac{20π}{3}\) cm.

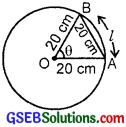
Question 6.
If, in two circles, arcs of the same length subtend angles of 60° and 75° at their centres, find the ratio of their radii?
Solution:

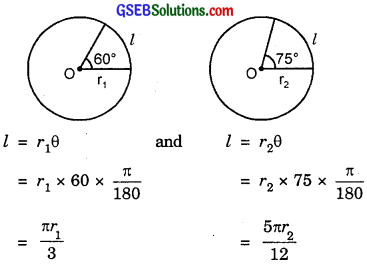
Since l is same for both the circles, therefore
\(\frac{π}{3}\)r₁ = \(\frac{5π}{12}\)r₂.
⇒ r₁ : r₂ = 5 : 4.

Question 7.
Find the angle in radians through which a pendulum swings, if its length is 75 cm and the tip describes an arc of length:

1. 10 cm
2. 15 cm
3. 21 cm

Solution:
1. r = 75 cm,
l = 10 cm,
θ = ?
⇒ θ = \(\frac{l}{r}\) = \(\frac{10}{75}\) radians.
= \(\frac{2}{15}\) radians

2. r = 75 cm,
l = 15 cm,
∴ θ = \(\frac{l}{r}\) = \(\frac{15}{75}\) radians = \(\frac{1}{5}\) radians.

3. r = 75 cm,
l = 21 cm,
∴ θ = \(\frac{l}{r}\) = \(\frac{21}{75}\) radians = \(\frac{7}{25}\) radians.