Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.2
Find the values of the other five trigonometric functions in questions 1 to 5:
1. cos x = – \(\frac{1}{2}\), x lies in third quadrant.
2. sin x = \(\frac{3}{5}\), x lies in second quadrant.
3. cot x = \(\frac{3}{4}\), x lies in third quadrant.
4. sec x = \(\frac{13}{5}\), x lies in fourth quardrant.
5. tan x = – \(\frac{5}{12}\), x lies in the second quadrant.
Solutions to questions 1 – 5:
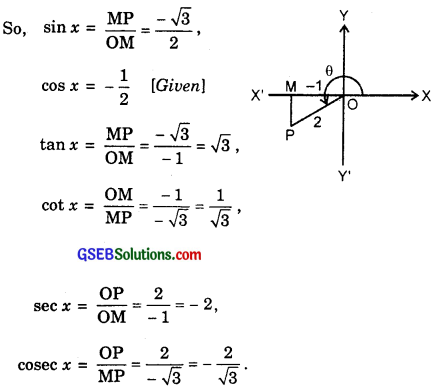
1. Since x lies in the 3rd quadrant, therefore
cos x = – \(\frac{1}{2}\) ⇒ \(\frac{OM}{OP}\) = \(\frac{- 1}{2}\).
Let OM = – 1 and OP = 2.
∴ MP = \(\sqrt{\mathrm{OP}^{2}-\mathrm{OM}^{2}}\) = – \(\sqrt{4 – 1}\) = – \(\sqrt{3}\)
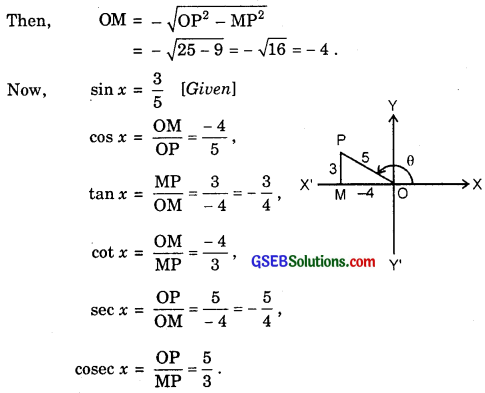
2. Since x lies in the second quadrant, therefore
sin x = \(\frac{3}{5}\) ⇒ \(\frac{MP}{OM}\) = \(\frac{3}{5}\)
Let MP = 3, S0, OP = 5.
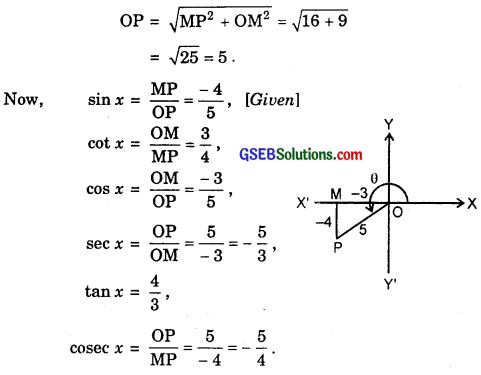
3. Since x lies in third quadrant, therefore
cot x = \(\frac{3}{4}\) = \(\frac{- 3}{- 4}\)
Let MP = – 4. So, OM = – 3. Then,
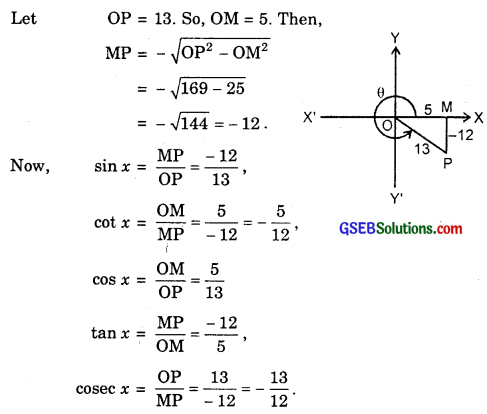
4. Since x lies in fourth quardrant, therefore
sec x = \(\frac{13}{5}\) ⇒ \(\frac{OP}{OM}\) = \(\frac{13}{5}\) [Given]
Let OP = 13. So, OM = 5. Then,
5. x lies in the second quadrant
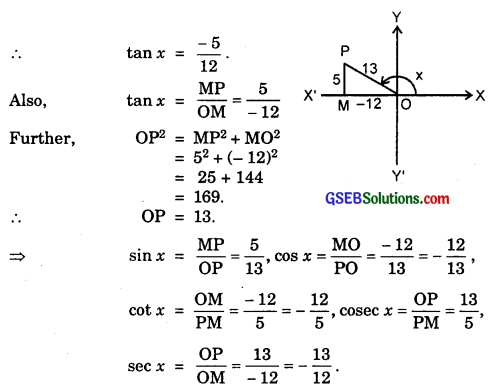
![]()
Questions?
Find the values of the following trigonometric ratios:
6. sin 765°
7. cosec (- 1410°)
8. tan \(\frac{19π}{3}\)
9. sin (\(\frac{-11π}{3}\))
10. cot (\(\frac{-15π}{4}\))
Solutions to questions 6 – 10:
6. sin 765° = (8 × 90° + 45°)
= sin 45° = \(\frac{1}{\sqrt{2}}\).
7. cosec (- 1410°) = – cosec 1410° [∵ cosec (-θ) = – cosec θ
= – cosec (16 × 90° – 30°)
= – cosec (- 30)° = – [- cosec 30°]
= cosec 30° = 2.
8. tan \(\frac{19π}{3}\) = tan (6π + \(\frac{π}{3}\)) = tan \(\frac{π}{3}\) = \(\sqrt{3}\).
9. sin (\(\frac{- 11π}{3}\)) = – sin \(\frac{11π}{3}\) [∵ sin(-θ) = – sin θ]
= – sin(4π – \(\frac{π}{3}\)) = – (- sin \(\frac{π}{3}\))
= sin \(\frac{π}{3}\) = \(\frac{\sqrt{3}}{2}\).
10. cot(\(\frac{- 15π}{4}\)) = – cot \(\frac{15π}{4}\) [∵ cot(-θ) = – cot θ]
= – cot (4π – \(\frac{π}{4}\)) = – cot (- \(\frac{π}{4}\))
= – (- cot \(\frac{π}{4}\)) = cot \(\frac{π}{4}\) = 1.