Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 6 Linear Inequalities Ex 6.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 6 Linear Inequalities Ex 6.2
Solve the following inequalities graphically in two dimensional plane:
1. x + y < 5 2.
2x + y ≥ 6
3. 3x + 4y ≤ 12
4. y + 8 ≥ 2x
5. x – y ≤ 2
6. 2x – 3y > 6
7. – 3x + 2y ≥ – 6
8. 3y – 5x < 30
9. y < – 2 10. x > – 3
Solutions to questions 1-10:
1. Consider the equation x + y = 5.
It passes through the points (5, 0) and (0, 5). The equation x + y = 5 is represented by AB. Consider the inequality x + y < 5.
Put x = 0, y = 0.
0 + 0 = 0 < 5,
which is true. Therefore, the origin 0 lies in the half plane x + y < 5.
∴ Shaded region shows or represents the inequality x + y < 5.
![]()
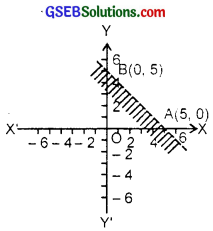
2. Consider the equation 2x + y = 6.
The line passes through (0, 6) and (3, 0).
The line 2x + y = 6 is represented by AB.
Now, 2x + y ≥ 6.
x = 0, y = 0 does not satisfy this inequality.
∴ Origin does not lie in the region of 2x + y ≥ 6.
Hence, the shaded area represents the inequality 2x + y ≥ 6.
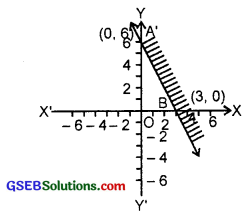
3. We draw the graph of the equation, 3x + 4y = 12. The line passes through the points (4, 0) and (0, 3). This line is represented by AB.
Now consider the inequality
3x + 4y ≤ 12
Putting x = 0, y = 0, we get
0 + 0 = 0 ≤ 12,
which is true.
∴ Origin lies in the region of 3x + 4y ≤ 12.
The shaded region represents this inequality.

![]()
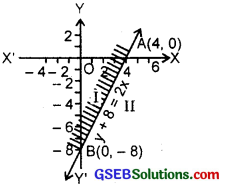
4. y + 8 ≥ 2x (Given inequality).
Let us draw the graph of the line.
y + 8 = 2x
Putting y = 0, x = 4. Therefore, point on the x-axis is (4, 0).
Again putting x = 0 in (1), y = – 8.
Hence, point on the y-axis is (0, – 8). AB is the graph of (1).
Putting y = 0, x = 4 in the given inequality, we have:
0 + 8 ≥ 0 or 8 ≥ 0, which is true.
Hence, origin lies in the half plane region I, i.e; Shaded region including the line is the solution region (see figure).
5. Given inequality is
x – y ≤ 2 ……………. (1)
Let us draw the graph of the line x – y = 2. …………….. (2)
Putting y = 0, x = 2. Hence, point on the x-axis is (2, 0). Again putting x = 0 in (2), y = – 2. Hence, point on they-axis is (0, – 2). So, AB is the graph of (2) (see figure).
Putting x – 0, y = 0 in (1), we have 0 – 0 ≤ 2 or 2 > 0, which is true.
Hence, origin lies in the half plane region. I, i.e., shaded portion including the line is the solution region (see figure).

![]()
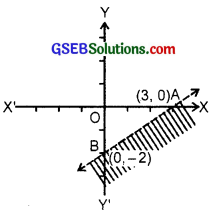
6. We draw the graph of 2x – 3y = 6.
The line passes through (3, 0) and (0, – 2).
AB represents the equation 2x – 3y = 6.
Now consider the inequality
2x – 3y > 6.
Putting x = 0, y = 0, we get
0 = 0 > 6 which is not true.
∴ Origin does not lie in the region of 2x – 3y > 6.
The graph of 2x – 3y > 6 is shown as shaded area.
7. Let us draw the line – 3x + 2y = – 6.
The line passes through (2, 0) and (0, – 3).
The line AB represents the equation – 3x + 2y = – 6.
Now, consider the inequality
– 3x + 2y ≥ – 6.
Putting x = 0, y = 0, we get
– 0 + 0 ≥ – 6, which is true.
Origin lies in the area denoted by the inequality – 3x + 2y ≥ – 6.
Graph of this inequality is shown in the figure by shaded area.

![]()
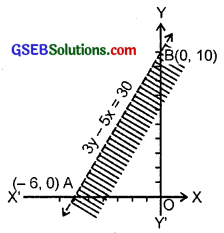
8. Given inequality is
3y – 5x < 30 ……………… (1)
Let us draw the graph of the equation 3y – 5x = 30 ………………….. (2)
Putting y = 0, x = – 6.
Hence, point on the x-axis is (- 6, 0). Again putting x = 0, y = 10.
Hence, the point on axis of y is (0, 10). So, AB is the graph of (2) (see figure).
Putting x = 0 and y = 0 in (1), we have:
0 – 0 < 30 or 30 > 0, which is true.
Therefore, origin lies in half plane region I. Shaded portion (excluding the line AB) is the solution region.
![]()
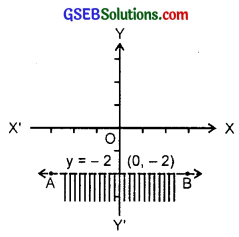
9. Given inequality is
y < – 2
Let us draw the graph of the line
y = – 2 (see figure).
AB is the required line.
Putting y = 0 in (1), we have
0 <- 2, which is not true.
The solution region is the shaded region below the line.
Hence, every point below the line AB (excluding the line) is the solution area.
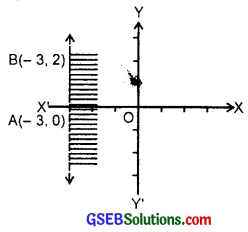
10. Let us draw the graph of x = – 3. The line passes through (- 3, 0), (- 3, 2). ∴ AB represents the line x = – 3. By putting x = 0 in the inequality x > – 3,
we get 0 > – 3, which is true.
∴ Origin lies in the region of x > – 3.
So, graph of the inequality x > – 3 is as shown in the figure by the shaded area.