Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 7 Permutations and Combinations Ex 7.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 7 Permutations and Combinations Ex 7.3
Question 1.
How many 3-digit numbers can be formed by using the digits 1 to 9, if no digit is repeated?
Solution:
3-digit numbers are to be formed.
i.e., Three places are to be filled with digits 1 to 9.
This can be done in 9 × 8 × 7
= 504 ways,

![]()
Question 2.
How many 4-digit numbers are there with no digit repeated?
Solution:
Let the digits be 0 to 9.
4-digit numbers are 10P4.
This includes those numbers which have 0 in the beginning (one thousand’s place)
3-digit numbers out of 9 digits 1-9 are 9P3.
∴ 4-digit numbers which do not have 0 in the beginning (on the extreme left)
= 10P4 – 9P3
= 10 × 9 × 8 × 7 – 9 × 8 × 7
= 9 × 8 × 7(10 – 1)
= 9 × 9 × 8 × 7
= 4536.
![]()
Question 3.
How many 3-digit even numbers can be made, using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?
Solution:
Let 2 be fixed at unit’s place.
Now, we have 5 digits and 3 places are to be filled up.
This can be alone in 5P2 ways.
When unit’s place is filled up both 4 or 6, again in each case, we have 5P3 numbers.
∴ 4-digit even numbers are
3 × 5P2 = 3 × 5 × 4
= 60.
Question 4.
Find the 4-digit numbers that can be formed, using the digits 1, 2, 3, 4 and 5, if no digit is repeated. How many of these will be even?
Solution:
(i) Out of 5 digits, 4-digit numbers are to be formed.
Such numbers are = 5P4 = 5 × 4 × 3 × 2
= 120.
(ii) When 2 is at unit’s place, then remaining three places are filled in 4P3 ways
= 4 × 3 × 2
= 24.
When 4 is at unit’s place, then 4-digit numbers are again = 24.
∴ Even 4-digit numbers
= 2 × 24
= 48.
![]()
Question 5.
From a committee of 8 persons, in how many ways can we choose a chairman and a vice chairman, assuming one person cannot hold more than one position?
Solution:
Out of 8 persons, chairman can be chosen in 8 ways. After selecting a chairman, we have to choose a vice chairman out of 7 persons.
This can be done in 7 ways.
Out of 8 persons, a chairman and a vice chairman can be chosen
8 × 7 = 56 ways.
Question 6.
Find n, if n-1P3 : nP4 = 1 : 9.
Solution:
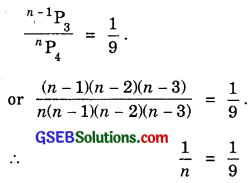
or n = 9.
![]()
Question 7.
Find r, if
(i) 5Pr = 26Pr-1
(ii) 5Pr = 6Pr-1
Solution:
(i) 5Pr = 26Pr-1
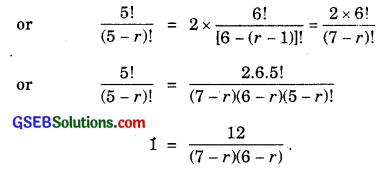
or (7 – r)(6 – r) = 12.
⇒ 42 – 13r + r2 = 12 or r2 – 13r + 30 = 0.
⇒ (r – 10)(r – 3) = 0 ⇒ r = 3 or 10.
r ≠ 10, since r cannot be greater than n.
∴ r = 3.
(ii) 5Pr = 6Pr-1

or (7 – r)(6 – r) = 6 or 42 – 13r + r2 = 6.
or r2 – 3r + 36 or (r – 9)(r – 4) = 0.
⇒ r = 9 or 4. So, r = 4, since r ≠ 9, because r cannot be greater than 4.
![]()
Question 8.
How many words can be formed using all letters of the word EQUATION, using each letter exactly once?
Solution:
Number of letters in equation = 8.
∴ Number of letters to be taken at a time = 8.
If p is the number of words thus formed, then
P = P(8, 8) = \(\frac{8!}{(8 – 8)!}\) = 8!
= 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 40320.
Question 9.
How many words, with or without meaning, can be made from the letters of the word MONDAY, assuming that no letter is repeated, if
(i) 4 letters are used at a time?
(ii) all letters are used at a time?
(iii) all letters are used but first letter is a vowel?
Solution:
(i) MONDAY has 6 letters. 4 letters are taken at a time.
∴ Number of words = 6P4
= 6 × 5 × 4 × 3
= 360.
(ii) All the letters of word MONDAY are taken at a time.
Number of words = 6!
= 6 × 5 × 4 × 3 × 2 × 1
= 720
(iii) Let the words begin with A.
Number of words formed with 5 letters = 5! = 120
Similarly, when words begin with ‘O’, number of such words = 120.
∴ Number of words beginning with vowel
= 2 × 120
= 240.
![]()
Question 10.
In how many of the distinct permutations of the letters in MISSISSIPPI, do the four ‘I’s not come together?
Solution:
In the given word their are 4I, 4S, 2P and 1M.
Total number of permutations with no restriction = \(\frac{11!}{4!4!2!}\)
If we take 4I as one letter, then total letters become = 11 – 4 + 1 = 8.
If p is the permutations, when 41s are not together, then
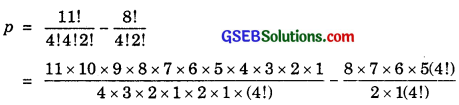
= 34650 – 840
= 33810.
![]()
Question 11.
In how many ways, can the letters of the word PERMUTATIONS be arranged, if the
(i) Words start with P and end with S?
(ii) Vowels are together?
(iii) There are always 4 letters between P and S?
Solution:
(i) Letters between P and S are ERMUTATION. These 10 letters having T two times. These letters can be arranged in \(\frac{10!}{2!}\) ways = 1814400 ways.
(ii) There are 12 letters in the word PERMUTATIONS which have T two times.
Now the vowels a, e, i, o, u are together.
Let it be considered in one block.
The letters of vowels can be arranged in 5! ways.
Thus, there are 7 letters and 1 block of vowels with T two times.
∴ Number of arrangements = \(\frac{8!}{2!}\) × 5! = \(\frac{8!5!}{2}\) = 2419200.
(iii) There are 12 letters to be arranged in 12 places.

These 12 letters are filled in 12 places as shown above.
P may be filled up at place No. 1, 2, 3, 4, 5, 6, 7 and consequently S may be filled up at place No. 6, 7, 8, 9, 10, 11, 12 leaving four places in between. Now P and S may be filled up in 7 ways. Similarly, S and P may be filled of in 7 ways.
Thus, P and S or S and P can be filled up is 7 + 7 = 14 ways.
Now remaining 10 places can be filled by E, R, M, U, T, A, T, I, O, N in \(\frac{10!}{2!}\) ways.
∴ No. of ways in which 4 letters occur between P and S
= \(\frac{10!}{2!}\) × 14 = \(\frac{3628800}{2}\) × 14 = 2540100.