Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 8 Binomial Theorem Ex 8.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 8 Binomial Theorem Ex 8.2
Find the coefficient of:
1. x5 in (x + 3)8
2. a5b7 in (a – 2b)12
Solutions to questions 1 and 2:
1. General term in (x + 3)8
= 8Crx8-r.3r
We have to find the coefficient of x5
8 – r = 5 ⇒ r = 8 – 5 = 3.
Coefficient of x5 (putting r = 3)
= 8C3.33 = \(\frac{8.7.6}{1.2.3}\).27 = 56.27 = 1512.
![]()
2. (a – 2b)12 = [a + (- 2b)]12
General term Tr+1 = C(12, r)a12-r(- 2b)r
Putting 12 – r = 5 or 12 – 5 = r ⇒ r = 7.
∴ T7+1 = C(12, 7)a12-7(- 2b)7
= C(12, 7)a5(- 2)7b7
= C(12, 7)(- 2)7a5 b7.
Hence, required coefficient is

= – 11 × 9 × 27 = – 99 × 8 × 128
= – 101376.
3. General term = Tr+1 = 6Cr(x2)6-r(- y)r
= (- 1)r\(\frac{6!}{r!(6 – r)!}\).x12-2r.yr.
![]()
4. Binomial expression is (x2 – yx)12.
∴ General term = Tr+1 = 12Cr(x2)12-r.(- yx)r
= \(\frac{12!}{r!(12 – r)!}\).x24-2r(- 1)ryrxr
= \(\frac{(-1)^{r} 12 !}{r !(12-r) !}\).x24-ryr.
5. Find the 4th term in the expansion of (x – 2y)12.
Solution:
4th term = T3+1 in the expansion of x + (- 2y)12
= 12C3x12-3(- 2y)3
= \(\frac{12.11.10}{1.2.3}\).x9(- 1)3.23.y3
= – 220 × 8x9.y3 = – 1760x9y3.
6. Find the 13th term in the expansion of (9x – \(\frac{1}{3 \sqrt{x}}\)18)
Solution:
13th term = T13 = T12+1 = 18C12(9x)18-12(- \(\frac{1}{3 \sqrt{x}}\))12

Find the middle term in the expansion of:
7. (3 – \(\frac{x^{3}}{6}\))7
8. (\(\frac{x}{3}\) + 9y)10
Solutions to questions 7 and 8:
7. Number of terms in the expansion is 7 + 1 = 8.
∴ There are two middle terms which are T4 and T5.
Hence, we are to find T4 and T5 in the given expansion.
(3 – \(\frac{x^{3}}{6}\))7 = [3 + (- \(\frac{x^{3}}{6}\))7
∴ Tr+1 = C(7, 3)37-r(- \(\frac{x^{3}}{6}\))r ………………… (1)
Now, Tr+1 = T4.
or r + 1 = 4
∴ r = 3.
∴ Putting r = 3 in (1), we have:

Again Tr+1 = T5 or r + 1 = 5.
⇒ r = 4
Putting r = 4 in (1), we get:

![]()
8. Number of terms in the expansion is 10 + 1 = 11.
Middle term of the expansion is \(\frac{11+1}{2}\) = T6.
Tr+1 = C(10, r)(\(\frac{x}{3}\))10-r (9r)r.
But Tr+1 = T6 or r + 1 = 6.
⇒ r = 5.
Putting r = 5 in (1), we have:
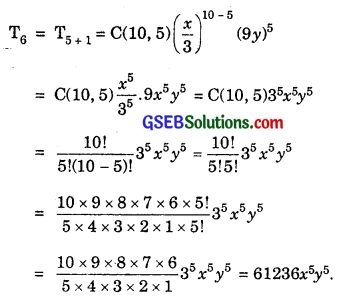
Question 9.
In the expansion of (1 + a)m+n, prove that coefficients of am and an are equal?
Solution:
General term in the expansion of (1 + a)m+n
= Tr+1 = m+nCrar.
Putting r = m
Tm+1 = m+nCmam ……………….. (1)
∴ Coefficient of am = m+nCm.
Again putting r = n, we get
Tn+1 = m+nCnan.
Coefficients of an = m+nCn
= m+nCm ………………….. (2) [∵ nCr = nCn-r]
From (1) and (2), coefficient of am is equal to coefficient of
am is equal to coefficient of an.
![]()
Question 10.
The coefficients of the (r – 1)th, rth and (r + 1)th terms in the expansion of (x + 1)n are in the ratio of 1 : 3 : 5. Find both n and r.
Solution:
General term in the expansion of (x + 1)n is
Tk+1 + 1 = C(n, k)xn-k.
Putting Tk+1 = Tr-1 or k + 1 = r – 1 or k = r – 2.
∴ Coefficient of Tr-1 is C(n, r – 2) ………………….. (1)
Putting Tk+1 = Tr or k + 1 = r, we get
k = r – 1.
∴ Coefficient of Tr is C(n, r – 1) ………………….. (2)
Putting Tr+1 = Tk+1, we get
r = k.
∴ Coefficient of Tr+1 = C(n, r)
According to the problem,

or 5r = 3 (n + 1 – r)
or 8r = 3n + 3 ………………… (5)
From (4) and (5),
2n + 10 = 3n + 3
or 3n – 2n = 10 – 3
From (5), 8r = 21 + 3 = 24
∴ r = 3
∴ n = 7, r = 3.
![]()
Question 11.
Prove that the coefficient of xn in (1 + x)2n is twice the coefficient of xn in (1 + x)2n-1.
Solution:
General term in the expansion of (1 + x)2n is
Tr+1 = C(2n, r)xr.
Putting r = n, we have:
Tn+1 = C(2n, n)xn.
Coefficient of xn = C(2n, n) ……………………. (1)
Again general term in the expansion of (1 + x)2n-1 is
Tr+1 = C(2n – 1, r)xr.
Putting r = n, we have:
Tn+1 = C(2n – 1, n)xn.
Coefficient of xn in the expansion of xn is C(2n – 1, n).
According to the problem, we are to prove that
C(2n, n) = 2 × C(2n – 1, n).

Multiplying numerator (N) and denominator (D) by n on R.H.S; we have:
= \(\frac{2n(2n – 1)!}{n!n(n – 1)!}\).
i.e; \(\frac{2n!}{n!n!}\) = \(\frac{2n!}{n!n!}\), which is true. (Proved)
![]()
Question 12.
Find a positive value of m for which the coefficient of x2 in the expansion of (1 + x)m is 6.
Solution:
Coefficient of x2 in the expansion of (1 + x)m is C(m, 2).
According to the problem,
C(m, 2) = 6.
or \(\frac{m(m – 1)}{2!}\) = 6
or m2 – m = 12
or m2 – m – 12 = 0
or m2 – 4m + 3m – 12 = 0
or m(m – 4) + 3(m – 4) = 0
or (m – 4)(m + 3) = 0
m = 4, since m ≠ – 3.