Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 8 Binomial Theorem Miscellaneous Exercise Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 8 Binomial Theorem Miscellaneous Exercise
Question 1.
Find a, b and n in the expansion of (a + b)n, if the first three terms of the expansion are 729, 7290 and 30375 respectively.
Solution:
T1 of (a + b)n = an = 729 ……………….. (1)
T2 of (a + b)n = nC1an-1b = 7290 ……………… (2)
T3 of (a + b)n = nC2an-2b2 = 30375 …………………. (3)
Dividing (1) by (2), we get

Dividing (2) by (3), we get

Dividing (4) by 5, we get
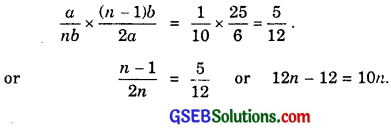
or 2n = 12 ⇒ n = 6.
Also, putting n = 6 in (1), we get a6 = 729 ⇒ a = 3
Putting n = 6 and a = 3 in (4), we get
\(\frac{3}{6b}\) = \(\frac{1}{10}\).
∴ b = \(\frac{3×10}{6}\) = 5.
Thus, a = 3, b = 5, n = 6.
![]()
Question 2.
Find a, if the coefficients of x2 and x3 in the expan sion of (3 + ax)9 are equal.
Solution:
General Term = Tr+1 = 9Cr.39-rarxr.
Putting r = 2, we get
Coefficient of x2 = 9C239-2.a2 = \(\frac{9×8}{2}\).37a2 = 4.39a2 …………………. (1)
Putting r = 3, we get
Coefficient of x3 = 9C339-3a3 = \(\frac{9×8×7}{6}\) × 36.a3
= 4 × 7 × 37.a3
Equating (1) and (2), we get
4.39.a2 = 4 × 7 × 37a3, we get
or 32 = 7a ⇒ a = \(\frac{9}{7}\).
Question 3.
Find the coefficient of x5 in the expansion of the product (1 + 2x)6(1 – x)7.
Solution:
(1 + 2x)6 = 6C0.1 + 6C1(2x) + 6C2(2x)2 +
6C3(2x)3 + 6C4(2x)4 + 6C5(2x)5 + 6C6(2x)6
= 1 + 12x + 60x2 + 20 × 8x3
+ 15 × 16x4 + 6 × 32x6 + 64x5
= 1 + 12x + 60x2 + 160x3
+ 240x4 + 192x5 + 64x5 …………………. (1)
(1 – x)7 = 1 – 7C1x + 7C2x2
– 7C3x3 + 7C4x4 – 7C5x5 + 7C6x6 – 7C7x7
= 1 – 7x + 21x2 – 35x3 + 35x4 – 21x5 + 7x6 – x7 …………………… (2)
Multiplying (1) and (2) and collecting the coefficients of x5, we get
Coefficient of x5 in the product (1 + 2x)0(1 – y)7
= 1 × (- 21) + 12 × 35 + 60 × (- 35) + 160 × 21 + 240 × (- 7) + 192 × 1
= – 21 + 420 – 2100 + 3360 – 1680 + 192 = 171.
![]()
Question 4.
If a and b are distinct integers, prove that a – b is a factor of an – bn, whenever n is a positive integer?
Solution:
Now a = a + b – b = b + (a – b)
an = b + (a – b)n
= bn + nC1an-1(a – b) + nC2bn-2(a – b)2 + ………………… + (a – b)n
or an – bn = nC1bn-1(a – b) + nC2(a – b)2 + ……………. + (a – b)n
= (a – b) = (a – b)[nC1bn-1 + nC2bn-2(a – b) + ……………. + (a – b)x-1]
Thus, (a – b) is a factor of (an – bn).
Question 5.
Evaluate (\(\sqrt{3}\) + \(\sqrt{2}\))6 – (\(\sqrt{3}\) – \(\sqrt{2}\))6.
Solution:
(\(\sqrt{3}\) + \(\sqrt{2}\))6 = (\(\sqrt{3}\))6 + 6C1(\(\sqrt{3}\))5(\(\sqrt{2}\))
+ 6C2(\(\sqrt{3}\))4(\(\sqrt{2}\))2 + 6C5(\(\sqrt{3}\))(\(\sqrt{2}\))5 + (\(\sqrt{2}\))5 ………………. (1)
(\(\sqrt{3}\) – \(\sqrt{2}\))6 = (\(\sqrt{3}\))6 – 6C1(\(\sqrt{3}\))5(\(\sqrt{2}\)) + 6C2(\(\sqrt{3}\))4(\(\sqrt{2}\))4
– 6C5(\(\sqrt{3}\))(\(\sqrt{2}\))5 + (\(\sqrt{2}\))5 ………………. (2)
Subtracting (2) from (1), we get
(\(\sqrt{3}\) + \(\sqrt{2}\))6 – (\(\sqrt{3}\) – \(\sqrt{2}\))6
= 2[6C1(\(\sqrt{3}\))5(\(\sqrt{2}\)) + 6C3(\(\sqrt{3}\))3 + 6C5(\(\sqrt{3}\))(\(\sqrt{2}\))5]
= 2[6.35/2.21/2 = 20.33/223/2 + 6.31/2.25/2]
= 2.31/2.21/2[6.32 + 20.33/223/2 + 6.31/2.25/2]
= 2.31/2.21/2[6.32 + 20.3.2 + 6.22]
= 2\(\sqrt{6}\) × 198 = 396\(\sqrt{6}\).
![]()
Question 6.
Find the value of (a2 + \(\sqrt{a^{2}-1}\))4 + (a2 – \(\sqrt{a^{2}-1}\))4.
Solution:
Put a2 = x, \(\sqrt{a^{2}-1}\) = y.
∴ (x + y)4 = x4 + 4C1x3y + 4C2x2y2 + 4C3xy3 + 4C4y4 ………………… (1)
(x – y)4 = x4 – 4C1x3y + 4C2x2y2 – 4C3xy3 + 4C4y4 ………………. (2)
Adding (1) and (2), we get
(x + y)4 + (x – y)4 = 2[x4 + 4C2x2y2 + 4C4y4] = 2[x4 + 6x2y2 + y4].
∴ (a2 + \(\sqrt{a^{2}-1}\)4 + (a2 – \(\sqrt{a^{2}-1}\))4
= 2[a2)4 + 6(a2)2(\(\sqrt{a^{2}-1}\))2 + (\(\sqrt{a^{2}-1}\))4].
= 2[a8 + 6a4(a2 – 1) + (a2 – 1)2]
= 2[a8 + 6a4(a2 – 1) + a4 – 2a2 + 1]
= 2[a8 + 6a6 – 5a4 – 2a2 + 1].
Question 7.
Find an approximation of (0.99)5, using the first three terms of its expansion?
Solution:
(0.99)5 = (1 – 0.01)5
= 1 – 5C1 × (0.01) + 5C2 × (0.01)2 ……
= 1 – 0.05 + 10 × 0.0001 ……
= 1.001 – 0.05
= 0.951.
![]()
Question 8.
Find x, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of (\(\sqrt[4]{2}+\frac{1}{\sqrt[4]{3}}\))n is \(\sqrt{6}\) : 1.
Solution:

Total number of terms = n + 1.
Fifth term from the end
= [(n + 1) – 5 + 1]th term from the beginning
= (n – 3)th term from the beginning

Dividing (1) by (2), we get

Question 9.
Expand using Binomial theorem (1 + \(\frac{x}{2}\) – \(\frac{2}{x}\))4, x ≠ 0.
Solution:

![]()
Question 10.
Find the expansion of (3x2 – 2ax + 3a2)3, using Binomial theorem?
Solution:
[3x2 – a(2x – 3a)]3
= (3x2)3 – 3C1(a2)2.a(2x – 3a) + 3C2(3x2)a2 – a3(2x – 3a)3.
= 27x6 – 27x4ax – 3a) + 9x2a2(4x2 – 12ax + 9a2)
– a3(8x3 – 3.4x2.3a + 3.2x9a2 – 27a3).
= 27x6 – 54x5a + 81a2x4 + 36a2x4 – 108a3x3
+ 81a4x2 – 8a3x3 + 36a4x2 – 54a5x + 27a6.
= 27x6 – 54ax5 + 117a2x4 – 116a3x3 + 117a4x2 – 54a5x + 27a6.