Gujarat Board GSEB Textbook Solutions Class 11 Physics Chapter 10 Mechanical Properties of Fluids Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Physics Chapter 10 Mechanical Properties of Fluids
GSEB Class 11 Physics Mechanical Properties of Fluids Text Book Questions and Answers
Question 1.
Explain why:
(a) The blood pressure in humans is greater at the feet than at the brain.
(b) Atmospheric pressure at a height of about 6 km decreases to nearly half its value at the sea level though the height of the atmosphere is more than 100 km.
(c) Hydrostatic pressure is a scalar quantity even though pressure is force divided by area.
Answer:
(a) The height of the blood column in the human body is more for the feet as compared to that for the brain. Consequently, the blood pressure in humans is greater at the feet than at the brain i.e. the blood exerts more pressure at the feet than at the brain.
(b) We know that the density of air is maximum near the surface o,f earth and decreases rapidly with height and at a height of about 6 km, it decreases to nearly half of its value at the sea level. Beyond 6 km height, the density of air decreases very slowly with height. Due to this reason, the atmospheric pressure at a height of about 6 km decreases to nearly half of its value at sea level.
(c) Since due to the applied force on the liquid, according to Pascal’s law, the pressure is transmitted equally in all directions inside the liquid. Thus there is ho fixed direction for the pressure due to liquid. Hence hydrostatic pressure is a scalar quantity.
![]()
Question 2.
Explain why:
(a) The angle of contact of mercury with glass is obtuse, while that of water with glass is acute.
(b) Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets and glass while mercury does not).
(c) Surface tension of a liquid is independent of the area of the surface.
(d) Water with detergents dissolved in it should have small angles of contact.
(e) A drop of liquid under no external forces is always spherical in shape.
Answer:
(a) When a small quantity of liquid is poured on glass, three interfaces namely liquid-air, solid-air and solid-liquid are formed. The surface tensions corresponding to these three interfaces i.e. TLA, TSA and TSL respectively are related to the angle of contact of a liquid with a solid as:
cos θ = \(\frac{\mathrm{T}_{\mathrm{SA}}-\mathrm{T}_{\mathrm{SL}}}{\mathrm{T}_{\mathrm{L}, \mathrm{A}}}\) ………………… (i)
In case of mercury-glass, TSA < TSL, therefore, from (i) cos θ is negative or θ > 90° i.e. θ is obtuse, But on the other hand, in case of water-glass, TSA > TSL, so from (i) cos θ is positive i.e. θ is less than 90° or acute.
(b) For equilibrium of a liquid drop on the surface of a solid, the equation TSA = TSL + TLA cos θ …………… (i) must be satisfied. For mercury-glass, angle of contact is obtuse. In order to achieve this obtuse value of angle of contact, the mercury tends to form a drop. But in case of water-glass, the angle of contact is acute, so equation (i) is not satisfied. In order to achieve this acute value of angle of contact, the water tends to spread.
(c) Surface tension is defined as the force acting per unit length on either side of an imaginery line drawn tangentially on the surface of the liquid. Since this force is independent of the area of the liquid surface, therefore surface tension is also independent of the area of the liquid surface.
(d) We know that the cloth has narrow spaces in the form of fine capillaries. The rise of liquid in a capillary tube is given by h = \(\frac{2Tcosθ}{rρg}\) i.e. h ∝ cos θ. It follows that if θ is small, cos θ will be large and detergent will rise more in the narrow spaces in the cloth. Now as detergents having small angles of contact can penetrate more, thus they will remove dirt from the cloth.
(e) In the absence of external forces, only force acting on the liquid drop is due to surface tension. A drop of liquid tends to acquire minimum surface area due to the property of surface tension. Since for a given volume of liquid, surface area is minimum for a sphere. So the liquid drop will always assume a spherical shape.
![]()
Question 3.
Fill in the blanks using the word(s) from the list appended wjth each statement.
- Surface tension of liquids generally ……………………….. with temperature, (increases/decreases)
- Viscosity of gases ………………………… with temperature, whereas viscosity of liquids with temperature. (increases/decreases)
- For solids with elastic modulus of rigidity, the shearing force is proportional to ………………………. while for fluids it is proportional to …………………. (shear strain/rate of shear strain)
- For a fluid in a steady flow, the increase in flow speed at a constriction follows from ……………………… while the decrease of pressure there follows from ……………………….. (conservation of mass/Bernoulli’s principle)
- For the model of a plane in a wind tunnel, turbulence occurs at a …………………………. speed than the critical speed for turbulence for an actual plane, (greater/smaller)
Answer:
- decreases.
- increases, decreases.
- shear strain, rate of shear strain.
- conservation of mass, Bernoulli’s principle.
- greater.
Question 4.
Explain why:
(a) To keep a piece of paper horizontal, you should blow over, not under it.
(b) When we try to close a water tap with our fingers, fast jets . of water gush through the openings between our fingers.
(c) The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection.
(d) A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel.
(e) A spinning cricket ball in air does not follow a parabolic trajectory.
Answer:
(a) If we blow over a piece of paper, velocity of air above the paper becomes more than that below it. As K.E. of air above the paper increases, so ,in accordance with Bernoulli’s theorem (P + \(\frac{1}{2}\) ρv2 = constant), its pressure energy and hence its pressure decreases: Due to greater value of pressure below the piece of paper = atmospheric pressure, it remains horizontal and does not fall. On the otherhand if we blow under the paper, the pressure on the lower side decreases. The atmospheric pressure above the paper will therefore bend the paper downwards. So the paper will not remain horizontal.
(b) This can be explained from the equation of continuity i.e. a1v1 = a2v2. As we try to close a water tap with our fingers, the area of cross-section of the outlet of water jet is reduced considerably as the openings between our fingers provide constriction (i.e. regions of smaller area). Thus velocity of water increases greatly and fast jets of water come through the openings between our fingers.
(c) According to Bernoulli’s Theorem, we know that
P + \(\frac{1}{2}\)ρv2 + ρgh = constant …………………. (i)
Here, the size of the needle controls the velocity of flow and the thumb pressure controls pressure. Now P occurs with power one and velocity (v) occuring with power 2 in equation (i), hence the velocity has more influence. That is why the needle of syringe has a better control over the flow rate.
(d) When a fluid is flowing out ofa small hole in a vessel, it acquires a large velocity and hence, possesses large momentum. Since no external force is acting on the system, a backward velocity must be attained by the vessel (according to the law of conservation of momentum). As a result of it, an impulse (backward thrust) is experienced by the vessel.
(e) This is due to Magnus effect:
Let a ball moving to the right be given a spin at the top of the ball. The velocity of air at the top is higher than the velocity of air below the ball. So according to Bernoulli’s Theorem, the pressure above the ball is less than the pressure below the ball. Thus there is a net upward force on the spinning ball, so the ball follows a curved path. This dynamic lift due to spinning is known as Magnus effect.
![]()
Question 5.
A 50 kg girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter 1.0 cm. What is the pressure exerted on the horizontal floor?
Answer:
Here, F = mg = 50 × 9.8 N = 490 N.
d = 1.0 cm
∴ r = \(\frac{d}{2}\) = 0.5 cm = 0.5 × 102m
= 5 × 10-3m
∴ Area of horizontal floor where the heel exerts is
A = πr2 = 3.142 × (5 × 103)2
= 3.142 × 25 × 10-6m2
∴ If P be the pressure exerted by the heel on the horizontal floor,
Then P = \(\frac{F}{A}\)
or P = \(\frac{490}{3.142 \times 25 \times 10^{-6}}\)
= 6.24 × 106Pascal
∴ P = 6.24 × 106Pa.
Question 6.
Torricelli’s barometer used mercury. Pascal duplicated it using French wine of density 984 kg m-3. Determine the height of the wine column for normal atmospheric pressure?
Answer:
P = Normal atmospheric pressure = 1.013 × 105 Pa
Let h be the height of the French wine column which earth’s atmosphere can support.
∴ If P’ be the pressure corresponding to height h of wine column,
Then, P’ = hρwg
where ρw = density of wine = 984 kg m-3
Now according to given statement
P’ = P
or hρwg = P
or h = \(\frac{P}{\rho_{w} g}\)
= \(\frac{1.013 \times 10^{5}}{984 \times 9.8}\)
= 10.5 m.
![]()
Question 7.
A vertical off-shore structure is built to withstand a maximum stress of 109 Pa. Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly 3 km, and ignore ocean currents?
Answer:
Here,
depth of water column, h = 3 km = 3 × 103 m.
density of water, ρ = 103 kg m-3.
If P be the pressure exerted by this water column at this depth,
Then P = hρg = 3 × 103 × 10 × 9.8
= 29.4 × 106Pa = 30 × 107 Pa.
= 3 × 107 Pa.
As the structure is put on the sea, sea water will exert upward thrust of 3 × 107 Pa.
Maximum stress which the vertical off-shore structure can withstand = 109 Pa.
Then 3 × 107 Pa < 109 pa
Thus we conclude that the structure is suitable as the stress applied by it is much lesser than the maximum stress it can withstand.
Question 8.
A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm2. What maximum pressure would the smaller piston have to bear?
Answer:
Here, the maximum force which the bigger piston can bear,
F = 3000kgf = 3000 × 9.8N
Area of piston, A = 425 cm2 = 425 × 10-4m2.
If P = maximum pressure on the bigger piston,
Then P = \(\frac{F}{A}\) = \(\frac{3000 \times 9.8}{425 \times 10^{-4}}\) = 6.92 × 105Pa
Since the liquid transmits pressure equally in all directions, hence the maximum pressure the smaller piston can bear ¡s 6.92 × 105 Pa.
Question 9.
A U-tubc contains water and methylated spirit separated by mercury. The mercury columns in the two arms are ¡n level with 10.0 cm of water in one arm and 12.5cm of spirit inthe other. What is the specific gravity of spirit?
Answer:
Here, for water column in one arm of U-tube:
h1 = 10.0cm
ρ1 = 1 gm cm3
For spirit column in other arm of U-tube,
h2 = 12.5cm
ρ2 = ?
if P1 and P2 be the pressures exerted by water column and spirit column respectively,
Then P1 = h1ρ1g ……………… (i)
and P2 = h2ρ2g …………………… (ii)

Also as the mercury columns in the two arms of U-tube are at the same level, thus in equilibrium,
P1 = P2
or h1ρ1g = h2ρ2g
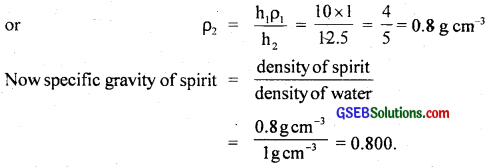
![]()
Question 10.
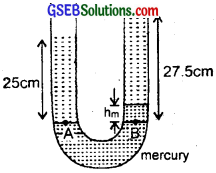
In the previous problem, if 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Specific gravity of mercury = 13.6).
Answer:
On pouring 15 cm of water and spirit each into the respective arms of the U-tube, the mercury level will rise in the arm containing the spirit.
ρm = density of mercury.
Let us select two points A and B lying in the same horizontat plane. Thus according to Pascal’s law,
Pressure at A = Pressure at B
or P0 + hwρwg = P0 + hsρsg + hmρmg
where P0 = atmospheric pressure
or hwρw = hs + hmρm
or hmρm = hwρw – hsρs …………………. (i)

Specific gravity of mercury = 13.6
Here, hw = height of water column
= 10 + 15 = 25 cm
hs = height of spirit column
= 12.5 + 15 = 27.5 cm
ρw = 1 g cm3
ρs = 0.8 g cm-3
ρm = density of mercury = 13.6 g cm-3
∴ From (i) and (ii) we get
hm × 13.6 = 25 × 1 – 27.5 × 0.8
or hm = \(\frac{25-22.00}{13.6}\) = 0.2206
= 0.221 cm.
or hm = 0.221 cm.
i.e. mercury will rise in the arm containing spirit.
Question 11.
Can Bernoulli’s equation be used to describe the flow of water through a rapid in a river? Explain?
Answer:
No, Bernoulli’s equation cannot be used to describe the flow of water through a rapid river. This is due to the reason that Bernoulli’s equation applies to streamline flow and in a rapid river, the flow of water is not streamline.
![]()
Question 12.
Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation? Explain?
Answer:
No, it does not matter if one uses gauge instead of absolute pressure in applying Bernoulli’s equation unless the atmospheric pressure at the two points where Bernoulli’s equation is applied are significantly different.
Question 13.
Glycerine flows steadily through a horizontal tube of length 1.5 m and radius 1.0 cm. If the amount of glycerine collected per second at one end is 4.0 × 10-3 kgs-1. What is the pressure difference between the two ends of the tube? (Density of glycerine = 1.3 × 103 kgm-3 and viscosity of glycerine = 0.83 Pas). (You may also like to check if the assumption of laminar flow in the tube is correct)
Answer:
Here, radius, r = 1.0 cm = 102 cm
length of tube, l = 1.5 m
Density of glycerine, ρ = 1.3 × 103kgm3
Mass of glycerine flowing per sec.,
M = 4 × 10-3 kg s-1
Viscosity of glycerine, η = 0.83 Pas = 0.83 Nm-2 s.
Let P = pressure difference between two ends of the tube = ?
Reynold number, N8 = ?
Let V = Volume of glycerine flowing per sec.
= 9.7537 × 102Pa
= 9.8 × 102Pa.
To check the assumption of laminar flow in the tube, let us find out the value of Reynold’s number given by

For Laminar flow, NR lies between 0 to 2000.
Now from (i) and (ii) we get

= 3.07 × 10-1 = 0.307 = 0.31
So the flow is laminar.
![]()
Question 14.
In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70 ms-1 and 63 ms-1 respectively. What is the lift on the wing if its area is 2.5 m2? Take the density of air to be 1.3 kg m-3?
Answer:
Let v1 and v2 be the speeds on the upper and lower surfaces of the wings of the aeroplane respectively, P1 and P2 be the pressures on the upper and lower surfaces of the wings respectively.
Here, v1 = 70 ms-1
v2 = 63 ms-1
ρ = 1.3 kg m-3
The level of the upper and lower surfaces of the wings from the ground may be taken same i.e. it is same.
∴ h1 = h2
area of wing, A = 2.5 m2
ρ = 1.3 kg m-3
Thus from Bernoulli’s Theorem,
P1 + ρgh1 + \(\frac{1}{2}\)ρv21 = P2 + ρgh2 + \(\frac{1}{2}\) ρv22
or P2 – P1 = \(\frac{1}{2}\) ρ(v12 – v22) …………………. (i)
This pressure difference provides the lift to the aeroplane i.e. lift on the wing.
Thus if F be the lift on the wing, Then
F = (P2 – P1) × A
= \(\frac{1}{2}\)ρ(v12 – v22) × A [by using (i)]
= \(\frac{1}{2}\) × 1.3 × (702 – 632) × 2.5
= \(\frac{1}{2}\) × 1.3 × 931 × 2.5 = 1512.9N
= 1.5129 × 103N = 1.513 × 103N
= 1.5 × 103N.
![]()
Question 15.
Fig (a) and (b) refer to the steady flow of a (non-viscous) liquid. Which of the two figures is incorrect? Why?
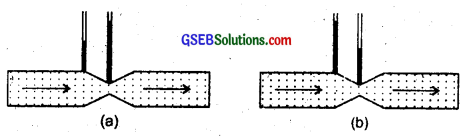
Answer:
Fig. (a) is incorrect. This is because at a constriction (smaller area or narrow part), the flow speed is larger due to mass conservation or equation of continuity for a non-viscous liquid (av = constant). Hence according to Bernoulli’s theorem, pressure in the narrow part must be low. But in this fig. the pressure at narrow part is shown to be larger.
Question 16.
The cylindrical tube of a spray pump has a cross-section of 8.0 cm2 one end of which has 40 fine holes each of diameter 1.0 mm. If the liquid flow inside the tube is 1.5 m min-1, what is the speed of ejection of the liquid through the holes?
Answer:
Here, area of corss-section of tube,
a1 = 8.0 cm2
= 8 × 104m2
No. of fine holes = 40
Diameter of each hole, d = 1 mm = 10-3 m
∴ r = radius of each hole = \(\frac{d}{2}\)
= 0.5 × 10-3m
∴ area of cross-section of each hole, a = πr2 = π(0.5 × 10-3)2 m2
∴ area of cross section of 40 holes,
a2 = 40 a = 40 π(0.5 × 10-3)2m2
v1 = 1.5 m/min. = \(\frac{1.5}{60}\) ms-1
Let v2 be the velocity of ejection of the fluid = ?
∴ according to equation of continuity,
a1v1 = a2v2

= 0.64 ms-1
![]()
Question 17.
A U-shaped wire is dipped in a soap solution and removed. The thin Soap film formed between the wire and a light slider supports a weight of 1.5 × 10-2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
Answer:
We know that a soap film has two free surfaces, so total length of the flim has two free surfaces, so total length of the film to be supported,
l = 2 × 30 cm
or l = 60 cm = 0.60 m
Let T = surface tension of the flim
If F = total force on the slider due to surface tension,
Then F = T × 2l = T × 0.6 N
W = 1.5 × 10-2N
In equilibrium position, the force F on the slider due to surface tension must be balanced by the weight (W) supported by the slider.
i.e. F = W = mg
or T × 0.6
= 1.5 × 10-2
∴ T = \(\frac{1.5 \times 10^{-2}}{0.6}\)
= 2.5 × 10-2 Nm-1.
Question 18.
Figure (a) shows a thin liquid film supporting a small weight = 4.5 × 10-2 N. What is the weight supported by a film of the same liquid at the same temperature in figure (b) and (c)? Explain your answer physically?
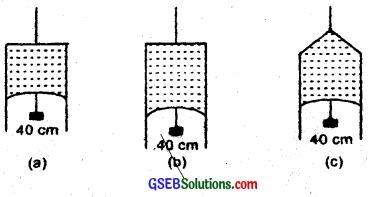
Answer:
(a) Here, length of the film supporting the weight l = 40 cm = 0.4 cm.
Total wieght supported (i.e.force) = 4.5 × 102 N
T = surface tension = ?
The film has two free surfaces, so total length,
L = 2l = 2 × 0.4 m
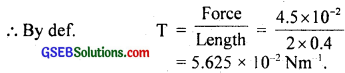
= 5.625 × 10-2 Nm-1.
Since the liquid is same for all the cases (a), (b) and (c) and temperature is also same, therefore surface tension for cases (b) and (c) will also be same. i.e. 5.625 × 10-2 Nm-1.
In Fig. (b) and (c), the length of the film supporting the weight is also the same as that of (a), hence the total weight supported in each case is 4.5 × 10-2 N.
![]()
Question 19.
What is the pressure inside the drop of mercury of radius 3.00 mm at room temperature? Surface tension of mercury at that temperature (20°C) is 4.65 × 10-1 Nm-1. The atmospheric pressure is 1.01 × 105 Pa. Also give the excess pressure inside the drop?
Answer:
Here, radius of drop, r = 3.0 mm = 3.0 × 10-3 m.
Surface tension of mercury, T = 4.65 × 101 Nm-1
Pressure outside the drop, P0 = Atmospheric pressure
= 1.01 × 105Pa
If pi be the pressure inside the drop, then excess of pressure inside the drop (p) is given by,
p = pi – P0 = \(\frac{2T}{r}\)
= \(\frac{2 \times 4.65 \times 10^{-1}}{3 \times 10^{-3}}\)
= 310 Pa
∴ pi = p + P0 = 310 + 1.01 × 105Pa
= 1.01 × 105 + 0.00310 × 105
= 1.01310 × 105Pa.
Since, the measurement are correct only upto 3 siginificant figures, Thus,
pi = 1.01 × 105Pa.
Question 20.
What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20°C) is 2.50 × 10-2 Nm-1? If an air bubble of the same dimension were formed at a depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 × 105 Pa).
Answer:
Surface tension of soap solution,
T = 2.5 × 10-2Nm-1
Density of soap solution, ρ = 1.2 × 103kg m-3
Radius of soap bubble, r = 5.0 mm = 5.0 × 10-3m .
1 atmospheric pressure = 1.01 × 105 Pa.
Excess of pressure inside the soap bubble is given by,
pi – P0 = \(\frac{4T}{r}\)
= \(\frac{4 \times 2.5 \times 10^{-2}}{5.0 \times 10^{-3}}\)
= 20 Pa
Excess of pressure inside the air bubble in the soap solution is:
pi – P0 = \(\frac{2T}{r}\)
= \(\frac{2 \times 2.5 \times 10^{-2}}{5.0 \times 10^{-3}}\)
= 10 Pa
Now pressure outside the air bubble at a depth of 40 cm is
P0 = Atmospheric pressure + pressure due to 40 cm
i.e. 0.4 m column of soap solution.
= 1.01 × 105 + 0.4 × 1.2 × 103 × 9.8
= 1.05704 × 105 Pa (∵ p = hρg)
= 1.06 × 105 Pa. (upto 3 significant figures)
∴ Pressure inside the air bubble,
Pi = P0 + \(\frac{2T}{r}\)
= (1.06 × 105 + 10)Pa
= 1.06 × 105 + 0.00010 × 105
= 1.06010 × 105Pa
= 1.06 × 105Pa (upto 3 siginificant figures).