Gujarat Board Statistics Class 11 GSEB Solutions Chapter 6 Permutations, Combinations and Binomial Expansion Ex 6.2 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Statistics Chapter 6 Permutations, Combinations and Binomial Expansion Ex 6.2
Question 1.
Obtain the values of the following:
(1) 11C4
Answer:
nCr = \(\frac{n !}{r !(n-r) !}\)
∴ 11C4 = \(\frac{11 !}{41(11-4) !}\)
= \(\frac{11 \times 10 \times 9 \times 8 \times 7 !}{4 \times 3 \times 2 \times 1 \times 7 !}\)
= \(\frac{7920}{24}\) = 330
(2) 9C0
Answer:
nC0 = 1
∴ 9C0 = 1
(3) 25C23
Answer:
nCr = \(\frac{n !}{r !(n-r) !}\)
∴ 25C23 = \(\frac{25 !}{23 !(25-23) !}\)
= \(\frac{25 !}{23 ! 2 !}\)
= \(\frac{25 \times 24 \times 23 !}{23 ! \times 2 \times 1}=\frac{600}{2}\) = 300
(4) 8C8
Answer:
nCr = 1
∴ 8C8 = 1
![]()
Question 2.
Find the unknown value:
(1) nC2 = 28
Answer:
nC2 = 28
∴ \(\frac{n !}{2 !(n-2) !}\) = 28
∴ \(\frac{n(n-1)(n-2) !}{2 \times(n-2) !}\) = 28
∴ n(n – 1) = 28 × 2
∴ n(n – 1) = 56
∴ n(n – 1) = 8 × 7
∴ n(n – 1) = 8(8 – 1)
∴ n = 8
(2) 27Cr+4 = 27C2r-1
Answer:
27Cr+4 = 27C2r-1
nCx = nCy
Or
n = x + y
27Cr+4 = 27C2r-1
∴ r + 4 = 2r – 1
∴ 4 + 1 = 2r – r
∴ r = 5
Or
r + 4 + 2r – 1 = 27
∴ 3r + 3 = 27
∴ 3r = 27 – 3
∴ r = \(\frac{27}{3}\) = 8
(3) nCn-2 = 15
Answer:
∴ \(\frac{n !}{(n-2) !(n-n+2) !}\) = 15
∴ \(\frac{n(n-1)(n-2) !}{(n-2) ! 2 !}\) = 15
∴ \(\frac{n(n-1)}{2}\) = 15
∴ n(n – 1) = 30
∴ n(n – 1) = 6 × 5
∴ n(n – 1) = 6(6 – 1)
∴ n = 6
(4) 4.nC4 = 7.nC3
Answer:
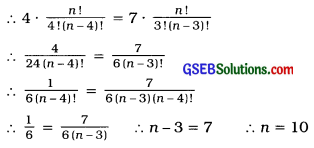
Question 3.
8 candidates applied for 2 posts of peon in a school. In how many ways can 2 peons be selected from 8 candidates?
Answer:
Total numbcr of combinations selecting 2 candidates for the post of peon out of 8 candidates
= 8C2
= \(\frac{8 !}{2 !(8-2) !}\)
= \(\frac{8 !}{2 ! 6 !}\)
= \(\frac{8 \times 7 \times 6 !}{2 \times 6 !}\)
=\(\frac{8 \times 7}{2}\) = 28
Alternative method:
8C2 = \(\frac{8 \times 7}{2 \times 1}\)
= 28
Question 4.
5 countries participate In a cricket tournament. In the first round, every country plays a match with the other country. How many matches will be played in this round?
Answer:
5 countries participate In a cricket tournament. Every country plays a match with the other country. Therefore, In every round two countries are selected to play a match.
∴ Total combinations = 5C2
= \(\frac{5 \times 4}{2 \times 1}\)
= 10 Matches
Question 5.
There are 200 items in a box and 5 % of them are defective. In how many ways can 3 items can be selected from the box so that all the items selected are defective?
Answer:
5 % of items are defective in a box of 200 items.
∴ No. of defective items in the box = 200 × \(\frac{5}{100}\) =10 items.
3 items are selected from the box. Such that all three items are defective.
∴ Total combinations = 10C2
= \(\frac{10 \times 9 \times 8}{3 \times 2 \times 1}\)
= \(\frac{720}{6}\) = 120
Question 6.
In how many ways can 3 clerks and 1 peon be selected from 14 clerks and 6 peons working in a bank?
Answer:
3 clerks out of 14 clerks can be selected in 14C3 ways and one peon out of 6 peons can be selected in 6C1 ways.
∴ Total combinations = 14C3 × 6C1
= \(\frac{14 \times 13 \times 12}{3 \times 2 \times 1}\) × 6
= 2184
![]()
Question 7.
There are 3 white and 5 pInk flowers in a box. In how many ways can
(1 ) three flowers of same colour be selected?
(2) 2 flowers of different colours be selected?
Answer:
In a box there are 3 white and 5 pInk flowers.
(1) Selected three flowers are of the same colour:
3 whIte flowers of 3 white flowers can be selected in 3C3 ways or
3 pink flowers of 6 pInk flowers can be selected in 6C3 ways.
∴ Total combinations = 3C3 + 5C3
= 1 + \(\frac{5 \times 4 \times 3}{3 \times 2 \times 1}\)
= 1 + 10 = 11
(2) Selected two flowers are of different colours:
1 white flowers out of 3 whIte flowers can be selected in 3C1 ways and
1 pink flower out of 5 pInk flowers can be selected In 5C1 ways.
∴ Total combinations = 1C1 × 8C3
= 3 × 5
= 15
Question 8.
Two cards are randomly selected from a pack of 52 cards. In how many ways can 2 cards be selected such that,
(1) both are of heart?
(2)one Is a king and the other is a queen?
Answer:
(1) In a pack of 52 cards, there are 13 cards of heart. 2 cards of heart out of 13 cards of heart can be selected in ways.
∴ Total combinations = 13C2 × 6C3
= \(\frac{13 \times 12}{2}\)
= 20
(2) In a pack of 52 cards, there are 4 cards of king and 4 cards of queen one card of king out of 4 cards of king can be selected in 4C1 ways and one card of queen out of 4 cards of queen can be selected In 4C1 ways.
∴ Total combinations = 4C1 × 4C1
= 4 × 4
= 16
Question 9.
There are 9 employees in a bank of whIch 6 are clerks, 2 are peons and 1 is a manager. In how many ways can a committee of 4 members be formed such that
(1 ) the manager must be selected?
(2 ) two peons are not to be selected and the manager Is to be selected?
Answer:
Out of 9 employces In a bank. 6 are clerks. 2 are peons and 1 Is a manager. A committee of 4 members Is to be formed.
(1) The manager must be selected In the committee:
If the manager Is to be selected In the committee of 4 members, than from the remaining (6 clerks + 2 peons) 8 employees, the remaining 3 members of the committee can be selected in 8C3 ways.
∴ Total combinations = 1C1 × 8C3
= 1 × \(\frac{8 \times 7 \times 6}{3 \times 2 \times 1}\)
= 56
(2) Two peons are not be selected and the manager is to be selected:
If the manager Is to be selected In the committee of 4 mcmbcrs and two peons are not be selected than from the remaIning 6 clerks, the remaining 3 members of the committee can be selected in6C3 ways.
∴ Total combinations = 1C1 × 6C3
= 1 × \(\frac{6 \times 5 \times 4}{3 \times 2 \times 1}\)
=20
Question 10.
In an office, there are 8 employees of which 3 are females and remaining are males. 3 employees are to be selected from the office for training. In how many ways can the selection be done so that at least one male Is selected?
Answer:
In an office, out of 8 employees 3 are females and 5 are males. 3 employees are to be selected for training.
The different options for selecting 3 employees so that at least one male is selected are as follows:
- One male and 2 females OR
- Two males and 1 female OR
- Three males and no female
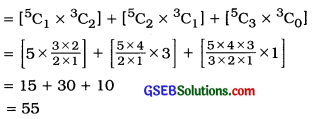
Question 11.
A person has 6 friends. In how many ways can he invite at least one friend to his house?
Answer:
A person has 6 friends. He wants to invite at least one of his friends to his house.
He may invite his 1 friend or 2 friends or 3 friends or 4 friends or 5 friends or 6 friends out of his 6 friends.
∴ Total combinations
= 6C1 + 6C2 + 6C3 + 6C4 + 6C5 + 6C6
= 6 + \(\frac{6 \times 5}{2 \times 1}+\frac{6 \times 5 \times 4}{3 \times 2 \times 1}+\frac{6 \times 5 \times 4 \times 3}{4 \times 3 \times 2 \times 1}\) + 6 + 1
= 6 + 15 + 20 + 15 + 6 + 1 = 63
![]()
Question 12.
In how many ways can 5 books be selected from 8 different books so that.
(1) a particular book is always selected?
(2) a particular books is never selected?
Answer:
Out of 8 different books, 5 books are to be selected.
(1) A particular book is always selected : If a particular book is always selected, then out of 7 remaining books, the remaining 4 books can be selected in 7C4 ways.
∴ Total combinations = 1C1 × 7C4
= 1 × \(\frac{7 \times 6 \times 5 \times 4}{4 \times 3 \times 2 \times 1}\)
= 35
(2) A particular book is never selected:
If a particular book is never selected, then out of the remaining 7 books, 5 books can be selected in 7C5 ways.
∴ Total combinations = 7C5
= \(\frac{7 \times 6 \times 5 \times 4 \times 3}{5 \times 4 \times 3 \times 2 \times 1}\)
= 21
Question 13.
A student in 12th standard commerce stream has to appear for exam in 7 subjects. It is necessary to pass in all the subjects to pass an exam. Certain minimum marks must be obtained to pass in a subject. In how many ways can a student appearing for the exam fail?
Answer:
A student has to appear for exam in 7 subjects. Certain minimum marks are required to pass in the subject. He fails if he does not reach to the level of minimum marks required in at least one of 7 subjects.
Total combinations in which a student can fail
= 7C1 + 7C2 + 7C3 + 7C4 + 7C5 + 7C6 + 7C7
= 7 + \(\frac{7 \times 6}{2 \times 1}+\frac{7 \times 6 \times 5}{3 \times 2 \times 1}+\frac{7 \times 6 \times 5 \times 4}{4 \times 3 \times 2 \times 1}+\frac{7 \times 6 \times 5 \times 4 \times 3}{5 \times 4 \times 3 \times 2 \times 1}\) + 7 + 1
= 7 + 21 + 35 + 35 + 21 + 7 + 1
= 127
Question 14.
In how many ways can a hotel owner subscribe 3 newspapers and 2 magazines from 8 different newspapers and 5 different magazines available in the city? If a particular newspaper is to be selected and a particular magazine is not to be selected then in how many ways can this selection be done?
Answer:
8 different newspapers and 5 different magazines are available in the city.
A hotel owner can subscribe 3 newspapers out of 8 newspapers in 8C3 ways and 2 magazines out of 5 magazines in 5C2 ways
∴ Total combination = 8C3 × 5C2
= \(\frac{8 \times 7 \times 6}{3 \times 2 \times 1}+\frac{5 \times 4}{2 \times 1}\)
= 56 × 10 = 560
If a particular newspaper is to be selected then 2 newspapers out of the remaining 7 newspapers can be subscribed in 7C2 ways and a particular magazine is not to be selected then 2 magazines out of the remaining 4 magazines can be selected in 4C2 ways.
∴ Total combinations = 7C2 × 4C2
= \(\frac{7 \times 6}{2 \times 1} \times \frac{4 \times 3}{2 \times 1}\)
= 21 × 6
= 126
Question 15.
If nP2 + nC2 = 84 then find the value of n.
Answer:
nP2 + nC2 = 84
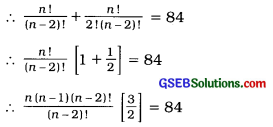
∴ n(n – 1) = 84 × \(\frac{2}{3}\)
∴ n(n – 1) = 28 × 2
∴ n(n – 1) = 56
∴ n(n – 1) =8 × 7
∴ n(n – 1) = 8(8 – 1)
∴ n = 8
![]()
Question 16.
If nPr ÷ nCr = 24 then find the value of r.
Answer:
\(\frac{n \mathrm{P}_{r}}{n \mathrm{C}_{r}}\) = 24
∴ \(\frac{\frac{n !}{(n-r) !}}{\frac{n !}{r !(n-r) !}}\) = 24
∴ r! = 24
∴ r! = 4 × 3 × 2 × 1
∴ r! = 4!
∴ r = 4